Goodbye Xinchou 题解

关羽下象棋

idea, solution from vfleaking, data from hehezhou

大家好，vfk 又来出题了 233 不过好像这次 FST 得有点惨。。哎，感觉这次出得不太好。

这道题既可以是一道猜结论题或者分类讨论题，也可以是一道暴力美学题。如果是我的话，在考场上我可能会当作暴力美学题来做，因为我会比较紧张；如果是平时自己做着玩的话，我会当一道分类讨论题来做。不过看到很多选手选择了分类讨论，却因为漏了情况而丢了不少分，我感到很惋惜。。

如果你回顾早年 UOJ 的 A 题，会发现都是些猜结论的题，而且还都有大牛十分钟就过了（但这道象棋题比以往的猜结论题复杂了许多）。我确实比较喜欢这类题吧。。因为我自己在赛场上有可能无法在短时间内那么机智地猜出结论，也许只会在做了一个小时之后才慢悠悠地提交上我的程序，所以我是真心觉得十分钟就过了当年猜结论类的 A 题的人很厉害。我一直觉得猜结论的能力本质上是一种计算机科学的直觉，或者数学直觉（类似于物理老师们强调的物理直觉）。真实世界的问题远比 OI 复杂，往往没有办法直接就做出来。很多时候确实是先得有人猜出来一个大致解法，然后再慢慢证明。所以说咯，直觉确实是个很重要的东西。

OIer 出比赛可能会有很多种不同的目的，比如展示自己的水平，比如分享自己的新想法，比如退役纪念。我的话，除了选题造题本身带给我的成就感之外，我会把比赛当作一种交流的途径。所以咯，当时我很喜欢把别人投来的猜结论题放到 UOJ 比赛里。大概想法就是，虽然我知道我有可能只会慢悠悠地做出来，但我就是想看看高手是怎么思考的，并学习学习。

不过这题不是别人投来的哈哈，我不确定我是否真的有出一道难度适中的猜结论题的水平，感觉这次有点翻车 ovo 啊所以，顺便征个题 233 欢迎来投小清新猜结论题呀！

好了下面我来讲讲我的思路（但并不是完全严谨的证明），也欢迎赛场上 AC 的同学们发发博客交流讨论。赛场上第一个用分类讨论的方式 AC 的应该是 Flying2018（提交记录链接），还有一位是 Foden47（提交记录链接）。所以强的人还是强啊！

算法一

第一个子任务里，车和卒是同一行的，显然车只要直接把卒吃掉即可。我猜肯定会有不想做博弈题直接跑路的选手 🤣 跑路之前这个部分分还是得拿一下呀，20分呢。

算法二

根据算法一的思路，如果卒和车在同一行或者同一列，我们直接输出 $1$ 。好了下面我们讨论 $x_{1} \neq x_{2}$ , $y_{1} \neq y_{2}$ 的情况。

诶，我们接着来看第……第……第四个子任务！为什么直接跳到了第四个呢，因为我们需要想想一般情况下这个题的答案到底是多少。想要分类讨论，就要先想想答案最大是多少。而在第四个子任务里，卒和车都在棋盘靠中心的位置，所以我们至少可以不用考虑棋盘边界对答案的影响。

先看有没有对称性可以利用 —— 诶，有。卒和车都是左右对称的，所以我们不妨设 $y_{1} < y_{2}$ ，即车在卒右边。如果 $y_{1} > y_{2}$ ，我们可以做一个水平的镜像对称。虽然不一定会体现在代码里，但至少思考的时候我们不用考虑车在卒左边的情况了。

现在我们随手画一个车在卒右边的情况：

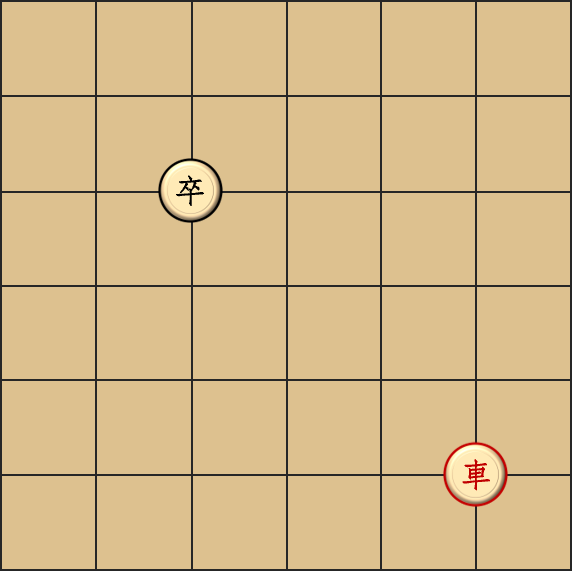
随手画一个

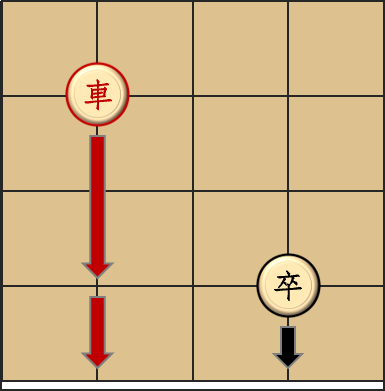
诶，然后我们来试试怎么把卒吃掉。我们先跑到卒的下面一行，这样卒就不敢往下走了，只能左右乱窜。然后我们就像样例一的第二组数据一样做：在卒的下面一行撒一行毒雾出来，卒仍然只能左右乱窜；现在我们跑到卒所在的那一行，卒仍然只能左右乱窜；接下来我们就把它吃掉。这样我们就得到了一个四步将卒吃掉的策略。

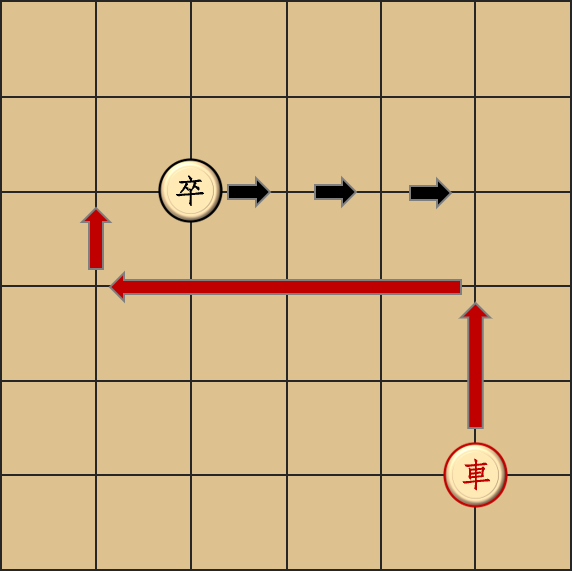
怎么把卒吃掉

努力枚举一番，你会发现你不可能找到一个三步的策略。等等，但为什么样例里最大值只有 3 呢。。。这确实是我们故意的，我们只放了答案小于等于 3 的情况。我们的本意是想区分开对着样例调的选手，和从头到尾先自己想再用样例检查正确性的选手，没想到导致了大片的 FST。（俗话说，出题人的嘴，骗人的鬼，所以还是不要轻信样例啊）

思考下这个策略，你会发现无论位置如何，你总能使用该策略。棋盘边界并不会有什么坏的影响，只会进一步压缩卒的移动空间，让答案小于等于 $4$ 而已。

不过我们现在在做第四个子任务，所以我们先不考虑边界的问题。那么，只要不在同一行同一列，就肯定是 4 了吗？如果卒和车离得很远的话，确实没有任何办法再优化 —— 首先如果卒既可以横向走，也可以向下走，那么卒肯定没办法在一步内被你吃掉，所以在吃掉卒之前，我们要么用毒封住卒的左右两侧，要么用毒封住下面。但封住左右两侧是需要走很多步的。因为如果你先封左边，卒可以往反方向走，导致你只能努力把它卡在某两列或者某三列，然后它就可以在里面继续乱走。经过一番尝试你会发现先封左侧或者先封右侧都是不可能比 4 步更优的。如果要封下面，那么晚封不如早封，所以就变成上图的那个策略了。

所以就是要考虑卒和车靠得很近的情况。可以发现，只要初始的时候不在卒所在的下一行，好像都没什么意义，还是得走到那行放毒。。如果在卒所在的下一行，那么上图的策略就可以省掉第一步了，于是 3 步就可以吃掉卒。（当然你看样例也会发现有这个情况）

特判掉这个情况，就可以过第四个子任务了。

if (x1 == x2 || y1 == y2) {
    return 1;
}
if (x2 == x1 + 1) {
    return 3;
}
return 4;

结合算法一，期望得分 40 分。

算法三

通过上述思路理清楚答案不超过 $4$ ，或者通过看样例之类的其他方式攒足了对“答案很小”的信心之后，你就可以使用暴力美学解决本题了。我认为也是比赛时最经济的一种做法。

因为答案不超过 $4$ ，所以卒之多只会走 $3$ 步，而车走到离卒太远的地方也毫无意义。

所以我们就可以在卒的初始位置附近，向各个方向延申常数格（仔细想想会发现常数取 $4$ 就足够了，不够自信也可以取一点，再逐步减小看看是否影响答案），然后只在这个小范围内进行搜索。如果车初始时不在这个范围内，不妨把车直接挪到离车最近的格点。

好的，迭代加深！博弈搜索！游戏规则也不是很复杂，按照题面把代码写出来就好了！赛场上大部分 AC 的选手正是用的这一暴力美学。

要注意的是搜索时我们要标记哪些位置是车曾经走过的。如果用布尔数组来存储，回溯时不方便还原。所以你可以用 int 数组存储每个位置被车经过的次数，这样递归时加加，回溯时减减就好了。

至于时间复杂度，你可以把所有可能的数据都试一遍，就会发现跑得贼快。这样大胆交一发，就直接过了。如果你使用的是这种做法，本题难点其实是你如何在尽量短的时间内，写出一份正确的博弈搜索代码。我看到有些选手的实现方式十分简洁，大家可以找来看看 233

一种实现下，搜索树的一个上界是 $1 + 39 + 39^{2}$ ，因为每一步为车的决策数最大为 $13$ ，卒最大为 $3$ ，并且如果第三步不能直接吃掉则可以剪枝。

期望得分 100 分。

算法四

下面我继续讲讲怎么通过分类讨论解决本题。

算法二已经解决了远离边界的情况，所以下面我们只用考虑边界问题。

由于卒不能往上走，所以上边界并没有什么用。而左右边界又是对称的，所以我们只用考虑左边界和下边界。（回忆下我们之前已经讨论过，只用考虑 $y_{1} < y_{2}$ 的情况）

思路大致如下。我们已知答案小于等于 4，而 1 的情况已经被我们判掉了，所以我们只用找出那些答案为 2 或者 3 的情况，剩下的就是 4。

首先思考一下什么情况会出现 $2$ 。已知车和卒不在同一行同一列，又已知车直接吃掉卒才会获得胜利，所以要想两步内取得胜利，那肯定一步也不能浪费。肯定是第一步先移动到卒所在的行或者列，然后再吃掉。但卒人家也不傻，如果他万一在车走了一步之后动了下，车就吃不到了。所以只有可能是卒的初始位置不佳，导致卒只能横向或者纵向移动，才会出现答案为 2 的情况。

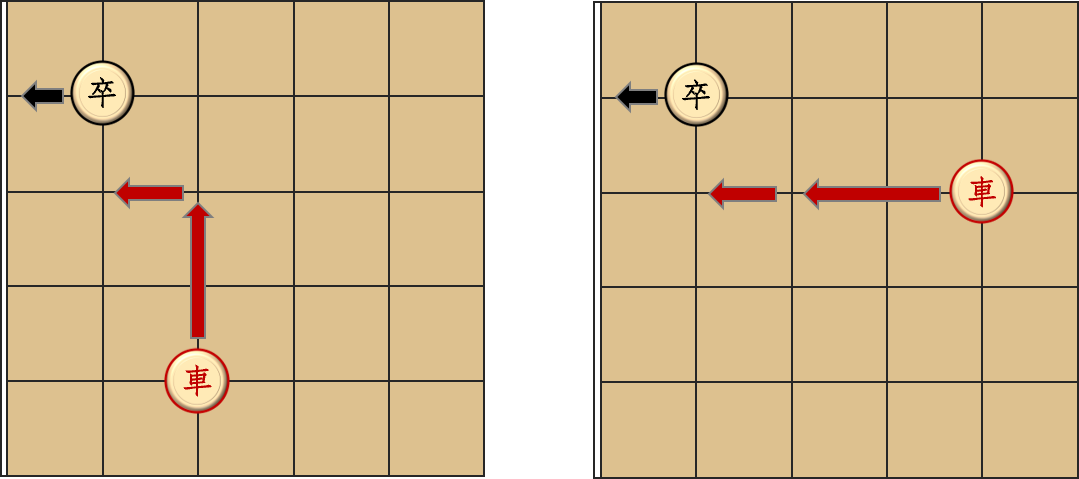
那么只有两种可能。要么卒的下边是棋盘边界，要么卒的左边是棋盘边界，如下图所示。一种情况是卒在最后一行，只能左右走。此时车走到卒所在的那一行，然后再花一步吃掉就好了。另一种情况是卒在第一列，比如 $(x, 1)$ ，并且车跟 $(x + 1, 2)$ 要么在同一行要么在同一列。此时车花一步走到 $(x + 1, 2)$ （或者该步选择不动），然后卒只能往右或者往下，但无论怎么走都会被车吃掉。

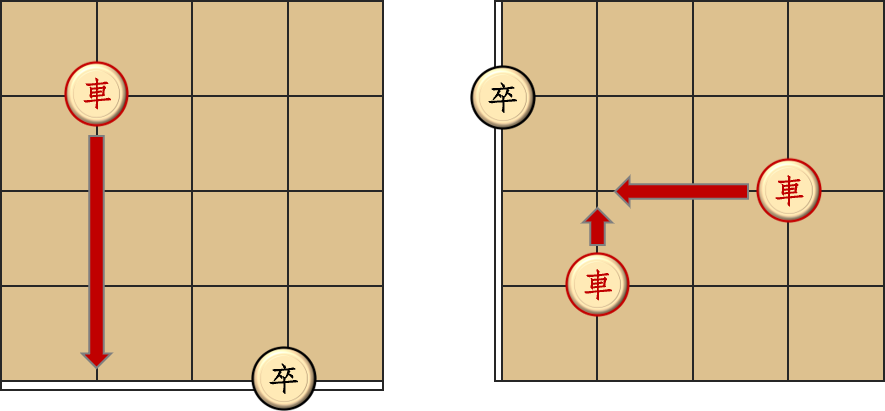
只有两种可能

还有别的情况吗？如果卒在第一列且不在最后一行，车跟 $(x + 1, 2)$ 既不在同一行也不在同一列，是否可以 2 步吃掉卒呢？枚举一番发现不行，但能发现一个 3 步的策略。首先我们把车移动到第二列。然后卒就只能往下走了，否则就会被立马吃掉。现在卒在 $(x + 1, 1)$ ，车在第二列。这瞬间就变回了前面讨论的 2 步吃卒的第二种情况：把车移动到 $(x + 2, 2)$ 的位置，那么接下来无论卒往下还是往右都会被车一步吃掉。

只有两种可能

综合上述讨论，虽然我们原本是想解决一下所有 2 步吃卒的情况，但似乎我们顺带解决了所有卒在第一列或者最后一行的情况了。这样就解决了第二和第三个子任务。

if (x1 == x2 || y1 == y2) {
    return 1;
}
if (y1 > y2) {
    y1 = m - y1 + 1;
    y2 = m - y2 + 1;
}
if (x1 == n) {
    return 2;
}
if (y1 == 1) {
    return x2 == x1 + 1 || y2 == 2 ? 2 : 3;
}
if (x2 == x1 + 1) {
    return 3;
}
return 4;

结合算法一算法二，期望得分 80 分。

算法五

我们离 AC 只有一步之遥了！这里只需要进一步讨论靠近棋盘边界的情况。但因为我们已经理清了答案小于等于 4 这一点，也找到了所有答案为 2 的情况，所以现在我们现在只用找出剩下的所有三步吃卒的情况就好了。

因为已经解决了第一列和倒数第一行的情况，所以我们只用接着考虑第二列和倒数第二行就好了。如果卒到边界的距离超过了 2 的话，只有卒在走第三步的时候边界才可能产生影响。然而我们讨论的是车是否可以三步吃卒，所以卒只能走两步。因此我们并不用考虑卒到边界的距离超过 2 的情况。

首先我们来讨论卒在倒数第二行的情况。我们只用枚举一下看看有没有三步吃卒的方案，结果发现还真有。我们只要把车挪到倒数第二行，那么卒如果左右动就会被立马吃掉，所以卒只能往下。这就变回了卒在最后一行的情况，我们只需要两步即可把卒吃掉：把车挪到最后一行，然后卒无论怎么动都会在下一步被吃了。

卒在倒数第二行

接下来我们来讨论卒在第二列的情况。类似卒在第一列的情况，我们可以注意到，如果卒在 $(x, 2)$ ，并且车跟 $(x + 1, 3)$ 要么在同一行要么在同一列，那么车可以在一步之内移动到 $(x + 1, 3)$ ，然后卒只能往左边走；车也往左边追一步，卒就只能往右或者往下了，然后就会被车在下一步吃掉。

卒在第二列

除此之外，只要第一步不通过某种方式阻止卒往右走，好像卒就会跑到第三列，然后就很难用所剩的 2 步吃掉卒了。所以就没办法了？

我出题的时候，第一次分类讨论就想到了这么多。然后码了一个暴力美学，结果发现 WA 了！

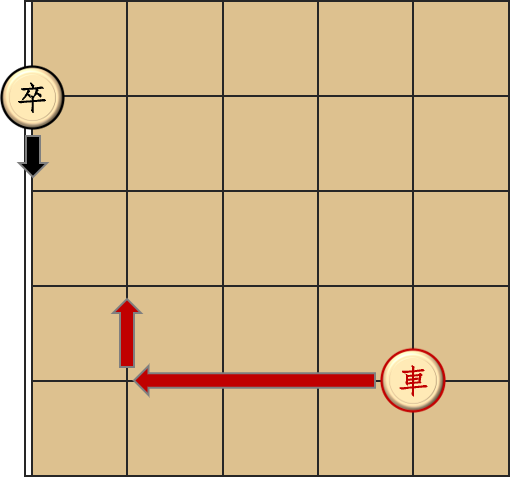
我漏掉的是这个情况：

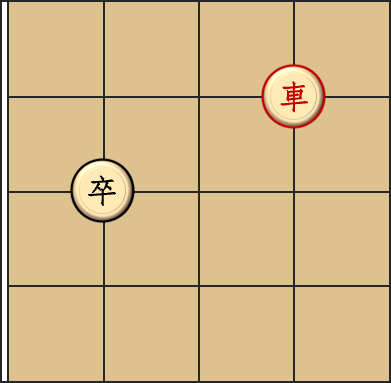
第二组的解释

眼熟吗？眼熟。因为这是样例一的最后一组数据。我发现自己都漏了这个情况之后灰溜溜把这种情况加入了样例，防止大家 FST。。。哎但最后发现样例还是给得太弱了。

这个情况下也是 3！为什么呢？这种情况不是没法阻止卒往右走吗？

确实，但这种情况可以绕个圈把卒困住！我感觉这实在有点妙 233 可能也是这道题最有趣的地方了。首先车先走到卒下方那一行，然后卒只能左右走，否则就会被吃掉。然后无论往左还是往右，车都移动到第二列。如果卒是往左走的，那么下一步无论向右还是向下都会被一步吃掉；如果卒是往右走的，那么卒现在向右和向下都被死死地封住了，所以只能往左，结果就会被一步吃掉。所以样例里的这种情况，三步就能吃掉卒。

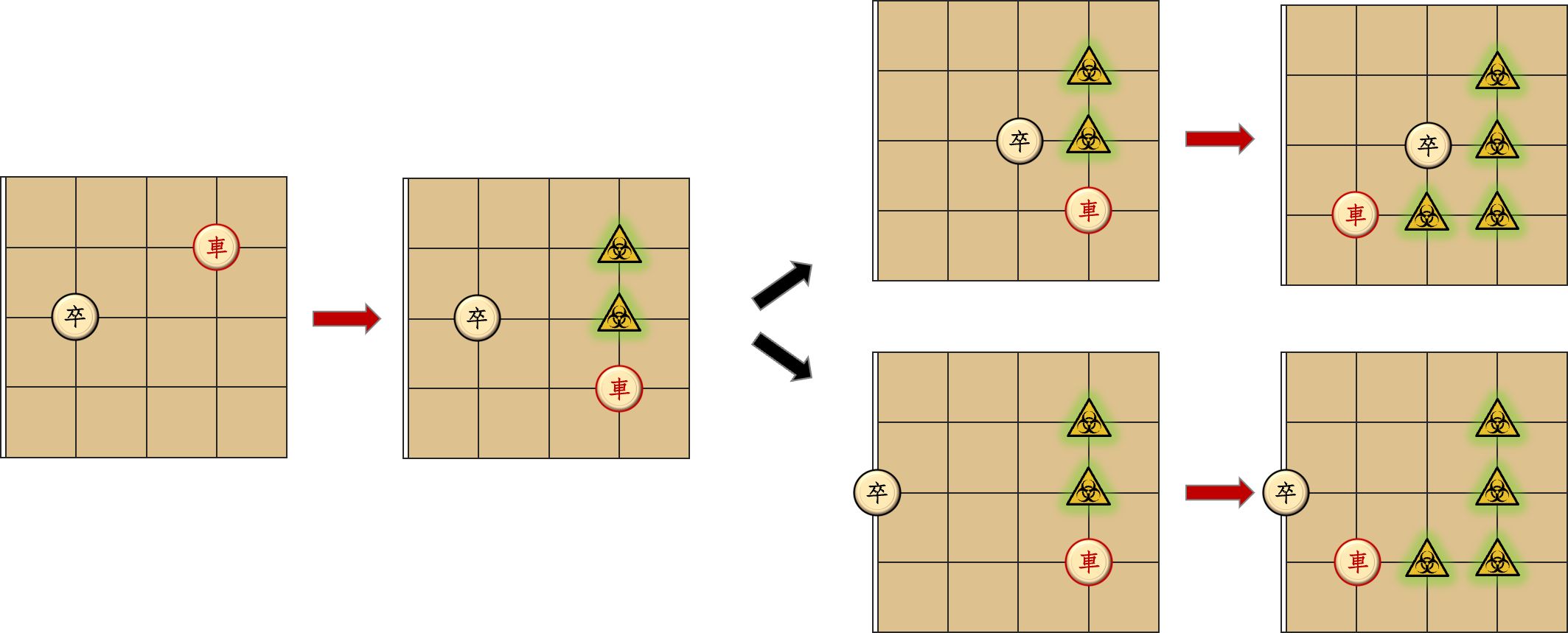
最有趣的情况

仔细想想，这种先围住然后再吃的情况只会发生在 $x_{2} \leq x_{1}$ 且 $y_{2} = 4$ 的时候。如果不是这种情况，卒第一步往右走之后，枚举一番可以发现至少会有一个不会被车立马吃掉的移动方向，所以就没法三步吃卒了。

综合上述所有情况，我们就可以写出代码，获得 100 分了：https://uoj.ac/submission/531552

写在最后

如果不是放在比赛时做，心平气和地分类讨论一番，再结合样例的提示，应该是可以一次写对的。个人也确实很喜欢这种抽丝剥茧的分类讨论，写对了还蛮开心的。但现在这么出导致了一大片 FST，好像确实不太好。。再次谢罪.jpg

张飞卷精兵

idea by LMoliver, vectorwyx, solution,std,data by hehezhou

算法一

爆搜所有安排方案。可以证明安排方案总种类数为 $\frac{2^{n}!}{2^{2^{n} - 1}}$ 。

复杂度 $O (\frac{2^{n}!}{2^{2^{n}}})$ ，可以通过子任务 $1$ ，期望得分 $10$ 分。当然略高的复杂度也可以打表提交来拿到相同分数。

算法二

考虑把对战建一棵树。每次对拼让赢家成为输家的父亲，点权即为初始卷力。那么答案就是奇数层权值之和减去偶数层权值之和。可以发现填数方案是合法的当且仅当父亲权值都大于儿子权值。考虑把权值从大到小填入，则这个过程可以看作：初始只有根解锁，一个被解锁的节点填入权值可以使它的儿子被解锁。

考虑一个贪心策略，如果当前能填入偶数层节点则直接填入，否则选一个节点填入，使得被解锁的节点数最多，如有多个任选即可。

这个策略是正确的！因为实际上如有多种选择，以这些节点为根的子树是同构的。考虑这棵树的构造方式。令 $T_{n}$ 为 $n$ 对应的树，显然有 $T_{0}$ 是单个节点， $T_{n}$ 的形态是一个根节点下挂了 $n$ 棵子树 $T_{0}, T_{1}, T_{2}, \dots, T_{n - 1}$ 。树上的所有节点可以按照儿子个数分成 $n + 1$ 类，则同类节点代表的子树彼此同构。

时间复杂度 $O (2^{n})$ ，可以通过子任务 $1, 2$ ，期望得分 $35$ 分。

算法三

考虑优化上述过程。将儿子个数为 $x$ 的节点称为 $x$ 类节点。

删去一个奇数层 $x$ 类节点将解锁偶数层 $0, 1, \dots, n - 1$ 类节点各一个，删去偶数层同理。那么在填入一个奇数层 $x$ 类节点后，会立刻填入 $x$ 个偶数层节点并解锁 $\frac{x (x - 1)}{2}$ 个奇数层节点： $x - 1$ 个 $0$ 类节点， $x - 2$ 个 $1$ 类节点， $\dots$ ， $1$ 个 $x - 2$ 类节点。

维护出当前解锁的奇数层每类节点有多少个，依次将 $n, n - 1, \dots, 0$ 类节点加入答案。计算贡献是等比数列求和的形式，可以在 $O (\log m o d)$ 的复杂度内完成，维护的信息需要对 $m o d - 1$ 取模。处理完节点贡献后，需要将产生节点加入已解锁节点。

时间复杂度 $O (n^{2} + n \log m o d)$ ，可以通过子任务 $1, 2, 3$ ，期望得分 $60$ 分。

算法四

考虑优化 $O (n^{2})$ 部分，即计算每类节点的贡献次数，显然可以通过维护若干信息的后缀和降至 $O (n)$ ，或通过打表发现较为简单的规律。

时间复杂度 $O (n \log m o d)$ ，可以通过本题，期望得分 $100$ 分。

赵云八卦阵

idea by orbitingflea, solution,std,data by QAQAutoMaton

算法一

我会记搜枚举所有合法方案！

期望得分 $10$ 分。

算法二

设最后得到的序列为 $b_{1} \dots b_{n}$ 。

注意到 $b_{i}$ 是 $a_{i} \oplus$ $a_{1} \dots a_{i - 1}$ 的一个子集。

对于每个 $i$ 枚举这个集合，然后算出lis。

时间复杂度 $O (n^{2} 2^{(\binom{n}{2})})$ ，期望得分 $10$ 分。

算法三

我会dp！

dp[i][j]表示前i个位置，长度为j的上升子序列，末尾的位置的最小值。

从i转移到i+1的时候枚举 $b_{i + 1}$ 的值，时间复杂度 $O (n^{2} 2^{n})$ ，期望得分 $30$ 分。

算法四

我会线性基！

我们发现， $b_{i}$ 取值是 $a_{1} \dots a_{i - 1}$ 的线性基能表示出来的值 $\oplus a_{i}$ 。

则我们可以在算法三的基础上，在线性基里查询满足 $> x$ 的最小 $b_{i}$ 。

时间复杂度 $O (n^{2} \log a)$ ，期望得分 $50$ 。

算法五

注意到当 $a_{i}$ 不能被加入线性基时， $a_{i}$ 能被前面的线性基表示出来，即可以认为 $a_{i} = 0$ 。这样的 $i$ 不超过 $\log a_{i}$ 段，每一段的线性基都一样。而 $a_{i}$ 能加入线性基的 $i$ 也不超过 $\log a_{i}$ 段。

考虑我们对前一种情况整段转移。

由于有更新的dp值一定在线性基中，所以我们可以对原来的dp值算出在线性基里的排名，然后比它大的最小值就是排名+1，以此类推。

整段转移直接用单调队列优化即可。

时间复杂度 $O (n \log^{2} a_{i})$ ，期望得分 $70$ 。

算法六

算法五的瓶颈在于在线性基里查询。

注意到任何时候 $b_{i}$ 都在 $a_{1} \dots a_{i}$ 的线性基中，所以我们dp只需要记末尾最小值在线性基中的排名。

对于整段转移的部分，我们就可以直接+1，对于更新线性基的情况，我们需要把排名转为新的排名。

注意到把线性基写成等价的最简形式（即每个元素的最高位依次为 $h_{1} > h_{2} > \dots > h_{k}$ 且除第 $i$ 个元素外其它元素的第 $h_{i}$ 位均为 $0$ ）后，一个数的排名就是它仅保留 $h_{1} \dots h_{k}$ 位后形成的 $k$ 位二进制数。

那么当一个数被插入线性基后，对旧元素的影响是让某些更高的位异或上了 $x$ ，则更新排名时只需要把更高位平移，并用builtin_parity求出 $x$ 对应位的取值即可。

接下来的单点转移，只需要求出最小的比某个dp值大的，满足某几位异或和是定值的数。可以类似的O(1)求出。

时间复杂度 $O (n \log a_{i})$ ，期望得分 $100$ 。

算法七

by QAQAutoMaton

$b_{i}$ 的取值是 $i - 1$ 前缀线性基能表示出来的所有值 $\oplus a_{i}$ ，则如果 $a_{i}$ 没被插入线性基， $b_{i}$ 的取值就是 $i$ 前缀线性基能表示出来的所有值

先从前往后把每个 $a_{i}$ 加入线性基，然后从后往前每次考虑加入一个新的 $b_{i}$ 。

对于一个没在线性基中的 $i$ ，可以注意到如果 $b_{i}$ 能被加入，把 $b_{i}$ 加入lis而非等到更小的 $j$ 再加入一定不劣，原因是对于所有 $j < i$ $b_{j}$ 的取值都是 $b_{i}$ 的子集。

所以只需要考虑在线性基中的i是否在lis中。

设在线性基中的位置为 $1 = k_{1} < k_{2} \dots k_{m} \leq n$ 。

可以发现相邻两个 $k_{j}$ 之间的 $i$ 取值集合是一样的，可以整段转移。

考虑dp[i][j]表示只考虑 $k_{i} \dots n$ 这一段后缀，在线性基的位置有 $j$ 个在lis中，不在的位置全在lis中，lis开头的最大值。

则我们整段转移的时候只需要定位到 $x$ 的排名 $y$ ，然后直接 $y, y - 1 \dots$ 即可，如果到1了就直接更新答案。

时间复杂度 $O (n \log a_{i} + \log^{3} a_{i})$ ，期望得分 $100$ 。

马超战潼关

idea by byqx, solution,data by he_____he , std by hehezhou

显然题意即为求一个经典二分图建图中的最小割个数。

算法 1

我会暴力！枚举每条边选或不选，检查是否是一个最小割即可。

时间复杂度 $O (2^{2 n + m} n^{2})$ ，可以通过子任务 1，期望得分 $5$ 分。

算法 2

我会比较好的暴力！令 $1$ 号点为源点， $2 n + 2$ 号点为汇点。

枚举每条与源点和汇点相连的边是否在割中，就能知道中间的边是否需要割。

时间复杂度 $O (2^{2 n} n^{2})$ ，可以通过子任务 1 和子任务 2，期望得分 $15$ 分。

算法 3

枚举左侧割了哪些边。对于右侧一个点，考虑有哪些左侧未被割开的点向这个点连边。如果总连边数量超过 $1$ 条，那么发现一定要割这个点与汇点之间连的边。如果总连边数量恰好为 $1$ 条，那么在这条边和到汇点的边之中一定恰好割其中之一。如果没有连边，不需要割边。发现右侧所有点均独立，直接相乘即可得到方案数。

时间复杂度 $O (2^{n} n^{2})$ ，可以通过前四个子任务，期望得分 $45$ 分。

算法 4

换一种方式看待问题。考虑先求出一种最大匹配的方案。可以发现，对于其中一个匹配 $(x, y)$ ， $S \to x \to y \to T$ 这三条边一定恰割一条。

枚举割哪条，看是否是个合法方案即可。

时间复杂度 $O (3^{n} n^{2})$ ，可以通过前三个子任务，期望得分 $35$ 分。

算法 5

仔细观察上一个算法，考虑什么样的方案是合法的。构造一个图，每个点代表一对匹配，用点权 $0, 1, 2$ 分别代表割 $S \to x$ ， $x \to y$ ， $y \to T$ 。设 $a_{x}$ 为 $x$ 所在匹配的点权。对于一条不在匹配的边 $(x, y)$ ，显然由匹配的最大性， $x$ 与 $y$ 至少有一个在匹配中。

如果 $x$ 与 $y$ 都在匹配中，则相当于不能有 $a_{x} = 1, 2$ 且 $a_{y} = 0, 1$ ，即 $a_{x} = 0$ 或 $a_{y} = 2$ 。
如果只有 $x$ 在匹配中，则相当于要求 $a_{x} = 0$ 。
如果只有 $y$ 在匹配中，则相当于要求 $a_{y} = 2$ 。

对于第一种情况，我们在 $x$ 和 $y$ 的匹配代表的点之间连一条有向边。

可以发现如果有一条边 $(u, v)$ ，那么 $a_{u} \leq a_{v}$ 并且不等于 $1$ 。所以相当于在这个有向图的任意一条链上，边权一定形如 $0, 0, \dots, 0, (1), 2, 2, \dots, 2$ 的形式。要求的即为分配点权的方案数。

枚举选 $0$ 的集合，需要满足不存在一条集合外连向集合内的边。发现 $1$ 只能放在所有集合外入度为 $0$ 的点中，并且对于所有点独立。只需检查集合外入度为 $0$ 的点个数即可。容易发现这实际上和算法 3 本质相同。

时间复杂度 $O (2^{n} n^{2})$ ，可以通过前四个子任务，期望得分 $45$ 分。

算法 6

我会爆搜！每次挑度数最大点爆搜，出现不同连通块就分开计算。

时间复杂度：？？？

期望得分 $35 \sim 100$ 。

算法 7

观察 $u_{2 i - 1} = u_{2 i}, v_{2 i - 1} = v_{2 i}$ 的条件有什么用。如果这两条边不在匹配中，那么和一条边没有区别。如果这两条边中有一条在匹配中，那么在算法 5 的有向图中会出现自环。自环说明这个点不能选 $1$ 作为点权。所以所有点点权只能为 $0$ 或 $2$ 。

再考虑图中的环。可以发现环上的所有点一定权值都相等，并且不能为 $1$ 。所以可以缩点，将图变为一个 DAG。将拓扑序求出，分为前一半和后一半。

枚举前一半哪些选 $0$ 哪些选 $2$ ，对于后一半的限制即为限制某些点必须选 $2$ 。预处理后一半的情况，做一次高维前缀和即可。

时间复杂度 $O (2^{\frac{n}{2}} n^{2})$ ，可以通过子任务 5，结合算法 5 可以获得 $65$ 分。

算法 8

现在每个点点权可以为 $1$ ，类似的，将图缩点之后分为拓扑序前一半和后一半。枚举前一半的情况，对于后一半的限制即为限制某些点必须选 $2$ 。一样高维前缀和预处理即可。

时间复杂度 $O (3^{\frac{n}{2}} n^{2})$ ，结合算法 7 可以通过前六个子任务，期望得分 $80$ 分。

算法 9

再仔细观察分为两半之后的过程。

如果只枚举前一半哪些选 $0$ 哪些选 $1$ 或 $2$ ，考虑以下两个问题：

前一半对后一半的影响
前一半内部的方案数

先看前一半内部的方案数如何求出。类似的，只有 $0$ 后面能选 $1$ ， $1$ 和 $2$ 后面不能选 $1$ ，所以选 $1$ 的只能是在 $1, 2$ 对应的导出子图中入度为 $0$ 的点。同样类似算法 5 中的分析，这些点互相独立，方案数即为 $2$ 的这么多次方。

再看前一半对后一半的影响。如果一个点为 $0$ ，那么对后面的点没有影响。如果一个点为 $1$ 或 $2$ ，那么要求出边对应的点只能选 $2$ 。所以相当于后一半中有一些点必须选 $2$ 。那么可以预处理出固定一些点选 $2$ 剩余点选 $0$ 或 $1$ 的方案数（这与前一半类似），再高维前缀和一次即可。

时间复杂度 $O (2^{\frac{n}{2}} n^{2})$ ，期望得分 $100$ 分。

黄忠庆功宴

idea, solution, std, data from djq_cpp

这道题出处其实是 chasedeath 问我的一道多项式题（？）大家似乎不太资瓷今年 Goodbye 出多项式，但感觉这个求和的部分本身也挺趣味就出出来了。原定是 D，由于出题人实在出不出困难而有趣的 E 就直接放 E 了，向广大 OIer 谢罪（雾

算法 1（std）

每次查询即求下标为模意义等差数列的 $a$ 之和。

考虑公差 $k$ ：若 $k \leq \sqrt{p}$ ，可以直接对每种 $k$ 预处理前缀和，复杂度 $O (p \sqrt{p} + q)$ ；另外，容易发现公差为 $k$ 的等差数列可以写成 $k^{- 1}$ 个公差为 $1$ 的等差数列的并，故若 $k^{- 1} mod p \leq \sqrt{p}$ ，原问题也可以用前缀和在 $O (p + q \sqrt{p})$ 时间解决。

进一步地，考虑将 $k$ 写成 $\frac{x}{y} mod p$ 的形式，其中 $1 \leq x, | y | \leq \sqrt{p}$ 。所有的 $k$ 均可写成这样的形式，这可以通过对集合 ${x - y k}$ 使用抽屉原理得到。进而只需对所有 $x$ 求出 $b_{i} = a_{i x mod p}$ 及其前缀和，再在序列 $b_{i}$ 上以 $O (y^{- 1})$ 的复杂度解决每个当前 $x$ 对应的询问，即可在 $O (p \sqrt{p} + q \sqrt{p})$ 的复杂度解决原问题。事实上，当 $p, q$ 不同阶时，通过调整 $x, y$ 的上界，易得一个 $O (p \sqrt{q})$ 复杂度的算法。

算法 1.1

根据观察场上许多选手的做法都与算法 1 基本一致，但选取的 $x$ 不是 $[1, \sqrt{p}]$ 而是 $O (\sqrt{p})$ 个随机值。事实上，这并不影响算法的期望复杂度，因为对每个公差 $d$ ，它对应的最小 $y$ 的期望都是 $O (\sqrt{p})$ 的。~~（虽然针对程序使用最劣的公差大概可以卡到多一个 $\log$ ）~~

（不过很多选手都因为常数问题只获得了 $55$ 分？这可能是因为随机化或者因为对下标模 $p$ 的处理不太漂亮？std 只要 1.1s，不过我是不是还是成为屑卡常出题人了）

算法 2 一些想法

笔者并未发现与算法 1 本质不同的可 AC 做法，不过从欧几里得算法的角度看，原问题等价于每次求 $a$ 与一个万能欧几里得序列的内积，从而或许还存在更本质的解法。遗憾的是，从这条路线出发，笔者目前只知道 $O ((p + q) p^{\frac{2}{3}})$ 的解法。感兴趣的选手可以自行思考，也欢迎与笔者讨论。

QAQAutoMaton的博客

博客