曹军大败潼关，被马超一众追击，割须弃袍，欲死里逃生！

为了封死曹操所有退路，马超欲设伏兵，行守株待兔之计。

在地图上：

1. 潼关附近的地图可以近似看成一个 $2n+2$ 个点的有向无环图。其中 $0$ 号点为潼关， $2n+1$ 号点为渭南。
2. $0$ 号点有到 $1,2,\cdots,n$ 号点的有向边，共计 $n$ 条。
3. $n+1,n+2,\cdots,2n$ 号点有连向 $2n+1$ 的有向边，共计 $n$ 条。
4. 除此之外还有 $m$ 条边，第 $i$ 条边为从 $u_i$ 到 $n+v_i$ 的边。其中 $1 \le u_i, v_i \le n$。
5. 不保证图中无重边。

现在马超想选取若干条路设置伏兵——由于西凉复杂的地形和曹军相比西凉庞大的兵力，如果在每条路都设计伏兵，则兵力分散，为下策。同时，通过曹军的内应，你知道了曹操会从潼关逃到渭南。因此，你必须保障无论曹军走什么路线都能遇见伏兵，同时设了伏兵的路要尽量少。

现在，马超想知道有多少种满足要求的设伏兵的方案。两种方案视为不同，当且仅当有一条路在一个方案里设了伏兵，另一个没有。

输入格式

第一行两个整数 $n,m$ 表示点数和额外的边数。

接下来 $m$ 行，第 $i$ 行两个整数 $u_i,v_i$，表示第 $i$ 条边为从 $u_i$ 到 $n+v_i$ 的边。

输出格式

输出一行，一个整数表示答案。

样例一

input

5 10
5 3
4 1
1 3
3 3
1 2
4 5
5 3
4 3
5 4
3 2

output

4

explanation

该样例对应的地图如下：

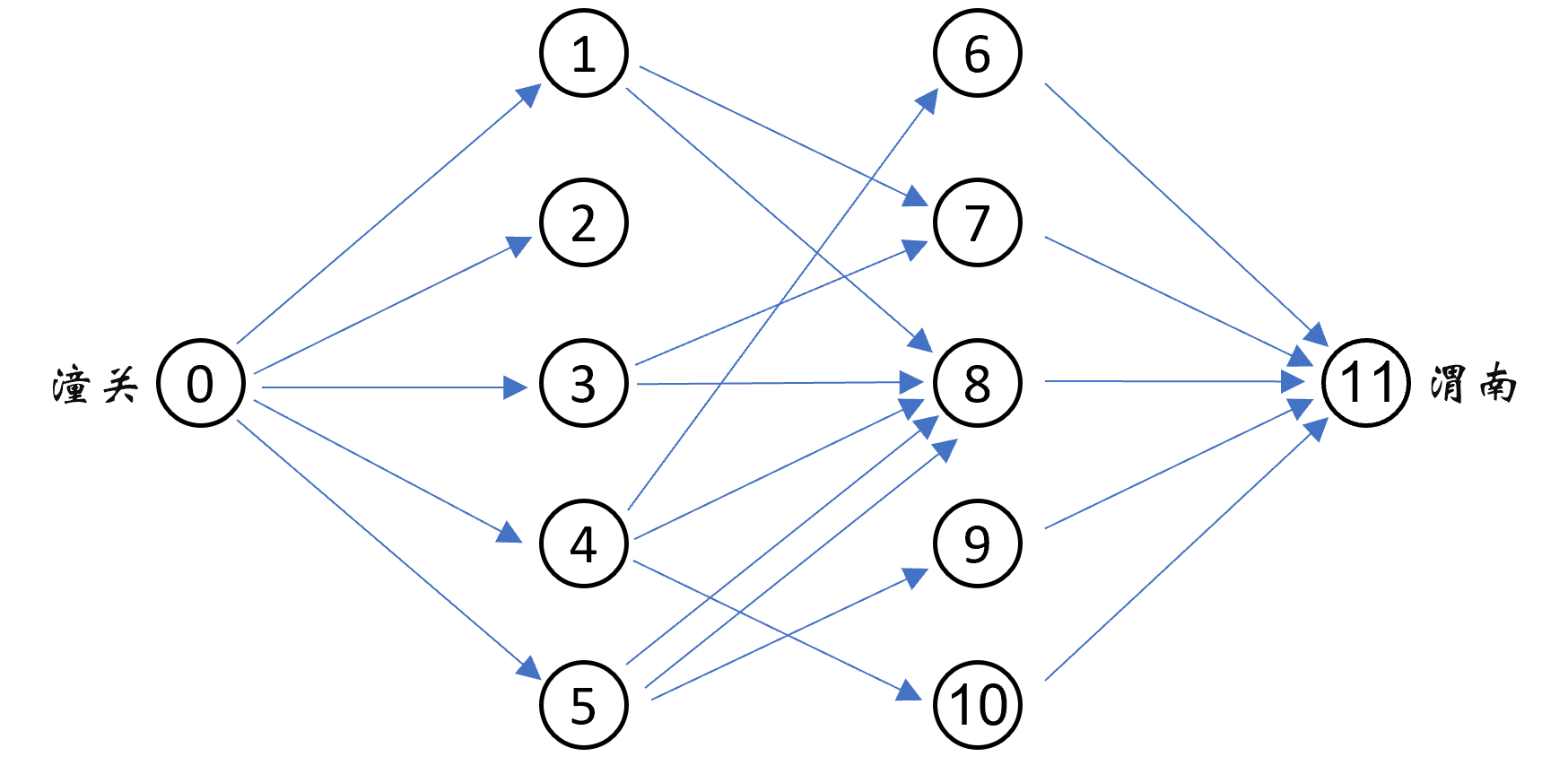
四种方案中设伏兵的边分别为：

1. $(0, 1), (0, 3), (0, 4), (0, 5)$；
2. $(0, 4), (0, 5), (7, 11), (8, 11)$；
3. $(0, 4), (5, 9), (7, 11), (8, 11)$；
4. $(0, 4), (7, 11), (8, 11), (9, 11)$。

样例二

见附件下载。

数据范围

对于所有数据，$1\leq n\leq 46,1\leq m\leq 400$。

时间限制：$\texttt{3s}$

空间限制：$\texttt{1GB}$