比特跳舞
idea, data, solution, std from csy2005
算法负二
对于特殊性质 A,长度为
可以通过子任务一,期望得分
算法负一
对于特殊性质 B,长度为
可以通过子任务二,结合算法负二期望得分
算法零
根据题意模拟,枚举每一对 std::set 里判断奇偶性即可。
时间复杂度为
算法一
考虑怎么求一个给定的序列
为了避免算重,对每个本质不同子序列,我们只在其最后一次在原序列中出现时计算它。
记
当
当
总共的本质不同子序列数即为
对于子任务四,枚举
时间复杂度为
算法二
考虑把算法一放到树上。
枚举
时间复杂度为
算法三
发现实际上每次在序列末尾插入一个元素时,
由于是树而不是链,我们仍需支持 dp 值的回退。但由于每访问一个点只修改一个值,我们只需记录这个值原来是多少即可,而无需记录整个 dp 数组。
时间复杂度为
算法四
我们还没有用到只需求出本质不同子序列个数的奇偶性而不是具体值这个性质。
观察我们刚才的 dp。记
考虑新增一个值
而
也就是说,新增一个值
初始时,
于是我们就有了一个暴力做法,每次枚举
时间复杂度为
算法五
由算法四中的结论可以得出,一个序列的本质不同子序列个数为奇数,当且仅当它可以划分为若干个长度至少是
考虑点分治。对于每一层,从分治中心开始 dfs,对每个点,求出其到分治中心的路径经过尽可能地删去是极短合法序列的前缀后,剩下的串的开头(或者这个串被删空)。对于两个在不同子树中的点,合法当且仅当它们剩下的串的开头相同或它们均被删空。
时间复杂度为
算法六
我们发现,
自反性和对称性是显然的,以下是传递性的证明:
根据算法五开头的判定方式,合法序列的拼接是合法序列,从合法序列中去掉一个合法的前/后缀得到的是合法序列。
设路径
和路径 的交是路径 , 的极长合法前缀是 , 的极长合法前缀是 , 的极长合法前缀是 。 若
,即 本身合法,那么 、 均是合法的,所以 是合法的。 否则
、 均是合法序列,于是得到 路径上的第一条边、 路径上的第一条边、 路径上的第一条边的边权均相等,且这三条路径上没有其他边的权值和它们相等,于是 是合法的,那么 也是合法的。
于是我们只需尽可能得合并等价类,然后计算每个等价类大小的平方和。
首先进行第一轮合并。考虑一个点
第一轮合并后,令每个等价类中最浅的点为这个等价类的代表(显然唯一),那么每个代表
实现时,我们通过自顶向下的 dfs 可以直接计算出每个点属于哪个等价类,故不需要使用并查集之类的数据结构来维护。
时间复杂度为
比特智慧
idea, data, solution, std from Sooke, solution2 from 127
题外话
出题人自以为设置了良心的部分分,未顾虑到临场选手的时间安排,对造成的不佳体验实感抱歉!
本题背景是抽芽游戏的变种 Planted Brussels Sprouts。鄙人不通现代处理技巧,仅给出些许古老但巧妙的推法,并不代表本题局限于此,请诸位尽情各显神通。
算法一
把题目的计数拆成两部分,我们相当于求所有能操作出的平面图的染色数之和。
手玩
算法二
有染色就有对偶图。不妨从
- “二分”:两侧接口均不使用,则两侧对偶图一定是孤立点,加边后对偶图仅一条边。
- “三分”:有一个接口不使用,则该侧对偶图是孤立点,加两条边,给另一侧对偶图接了个三角形。
- “四分”:两侧接口均被使用,加两条边,相当于拼接两侧对偶图,中间形成了个四边形。
稍加归纳,我们得出
进一步地,
显然,用
故暴力枚举所有能操作出的平面图,用上式统计答案,可以通过子任务
算法二点五
我们希望找到一种对应关系,能够描述操作结果而不计过程,从而使计数不重不漏。注意到操作不改变空接口的数量,由此想到为初始的接口顺次标号
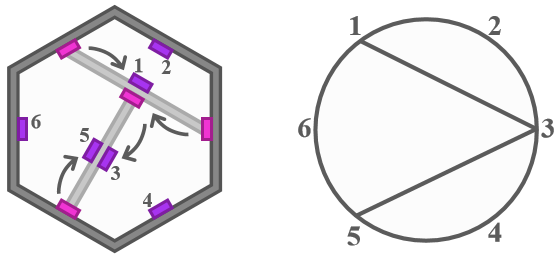
那么任意时刻的操作局面,都能映射为边不交叉的操作树(森林)。这是否构成双射?答案是肯定的。圆上连边情况亦可实现反推,对于圆上点
由算法二的式子得知,“四分”是影响最终局面染色的关键,我们需要迁移“四分”的定义至操作树(森林)上。回顾后发现,编号为
算法三
该算法是出题人最原始的做法,但是与正解相差甚远,有需要者请跳到算法 4!之所以单独列出,是因为该算法同样极具趣味性。
还是从
将块编号为
分配标号,系数为
考虑第
接下来是最重要的圆上排列部分。在 CF1172B - Nauuo and Circle 中,我们知道排列方案数等于各点度数的阶乘之积乘上
最终总和乘上上述结论的
我们先作一些初等的简化:
看似无法再推下去,但有趣的是,括号内的式子存在组合意义。将分式写成组合数
于是原式可再度简化为:
里面还是三项式系数。我们如法炮制,
现在试图表示总答案。令
奇迹般地,我们整理出二项式系数,对上式作最后的化简:
实现多项式快速幂即可,时间复杂度
算法四
算法三的遗憾在于只能求单点,而难以批量处理所有
不妨钦定操作树的
- L 儿子:
- R 儿子:
然后我们构造一棵三叉树,各点的三叉具体包含:
- 一或零条 / 边:连接第一个 L 儿子,若无 / 边则无 L 儿子。
- 一或零条 | 边:连接第一个 R 儿子,若无 | 边则无 R 儿子。
- 一或零条 \ 边:若自己是某个点第
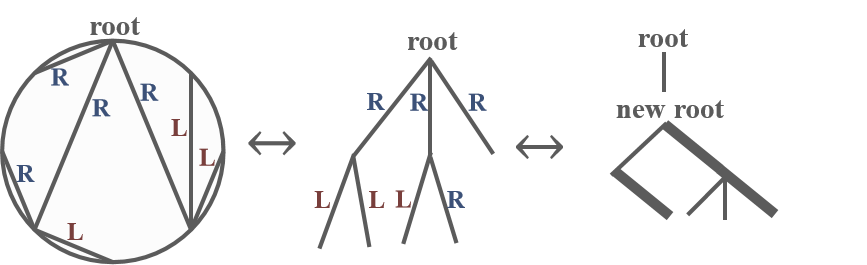
由于原根结点
下一步自然是再次迁移“四分”的定义。显然,圆上每个点的标记规律是:若有 R 儿子,标记与第一个 R 儿子间的边,若无 R 儿子,则标记父边。那么三叉树上一条边欲代表“四分”,首先自身不能是 | 边,否则会被父结点标记,其次子结点必须有 | 边,否则会被子结点标记。也即,“四分”数等价于三叉树符合以下结构的边的子集数:

于此多项式的引入便不言而喻了。定义一个三叉树的权值为
稍加化简可得:
套用经典的牛顿迭代即可。时间复杂度
实际上,若将算法三中的
算法五
从
惊人结论是,排列方案数等于
时间复杂度
另解
下面为 zhoukangyang 所分享的 B 题题解: https://www.cnblogs.com/zkyJuruo/p/17136175.html 。在此表达感谢!
另·另解
下面为 hos_lyric 所分享的 B 题题解: https://hos-lyric.blog.uoj.ac/blog/8415 。在此表达感谢!
比特之地
idea, data, solution, std from 127
算法一
对于第一个子任务,使用暴力 BFS 计算点对间距离。
时间复杂度为
算法二
按照路径经不经过根进行分类讨论,距离即为曼哈顿距离。
期望通过子任务二,得到
算法三
对于第三个子任务,可以使用沿中线分治/线段树维护矩乘的方法解决。
期望通过子任务三,得到
算法四
对于第四个子任务,图等价于网格图,按任意行列切开均可,如果想要刨去根,只需先对根做一次bfs,再算经过根对答案的贡献即可
期望通过子任务二、三、四,得到
算法五
原本四年前出的这题,直到找到了separator theorem才发现可做。
可以认为是平面图最短路Oracle,存在更优的做法,而像是有时遇到的像高分子聚合物一样的图都可以使用。
按照separator theorem的想法,我们要去找尽可能优的separator,但是此图有一个好处,即bfs树就是原树。
因此我们可以获取很大的便利。
首先若树高不超过
考虑为什么这样是separator,在dfs序上,这些点将序列分为很多个部分,则每两个部分之间的点的深度的max在所选的separator中取到,则跨过最初的中位点的到根链的部分之间的所有深度被separator取到,即一定会经过我们选择的separator。
若树高高于
然后我们中间的设计不按照原定理去做,按照我们上面所述的树高不高的方法做即可。
找到了separator我们按照其分裂原图,分治下去,并计算经过这些点的最短路贡献答案。
时间复杂度是
不过这样可能会导致一些问题,比方说其实我们当前分治到的部分不是一个原树上的连通块,而应当用很多个原树上的连通块及其之间的横边表示,需要进行一些处理。
多使用vector进行找separator的过程会好写,不是瓶颈。
期望通过所有子任务,得到
算法六
实际上,笔者观察到选手所写的代码,发现非常有道理。
这是因为,实际上separator定理在本题中不需要是一整个separator,也就是分成三部分完成separator的构造,只不过三次取的界限应当比较一致。
因此简单认为每次只分横竖都是有道理的。
期望通过所有子任务,得到

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号