如下图所示，比特之地是在一颗土豆地雷发达的根系上建立的。

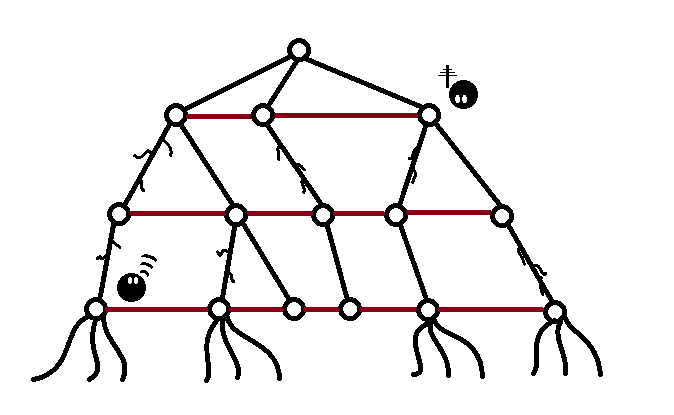
起初这些根系只是越来越多，在地下形成了一个复杂的网络。形式上，这些根系形成了一棵向下的树。

当比特族的祖先地底漂泊到这里的时候，决定在这里建立比特的家园，按照树的顺序在对应的位置修砌了房屋。这些位置可以被视作树上的节点，节点之间由根系相连，可以视作树中的边。特别地，最接近地面的节点唯一，且被称为根节点。

比特族的祖先将比特的家园建造得井井有条。具体地，这棵树满足以下性质：

• 一条边连接的两个节点中，较深的节点的编号更大。

• 以每个点为根的子树的编号都是一段连续的区间。

• 对于同一层的点，左边的点编号比右边的小。

时至今日，比特们通上了信息高速路。比特国网络服务公司在原有的根系，也就是树边上铺设了光纤，这样所有节点的比特们都可以通信。

为了使得通信网络更加稳固，公司又在比特之地中左右相邻的同层节点之间拉好光纤（图中棕色边）。这里一个节点的层数是指它到根节点所经过的边数。

现在，苦读通信工程的你接到了帮助比特国估算网络延迟的任务。

具体来说，你决定好了 $Q$ 个关键通信任务，每个任务给出一对节点 $(x,y)$，你需要计算 $(x,y)$ 间通信最少需要途径多少条光纤。

形式化题意：

给定一棵有根树，编号为 $1\sim n$，根节点为 $1$，每条树边长为 $1$，定义每个节点的深度为到根经过的边数。保证存在一个 dfs 序，使得编号为 $i$ 的点是 dfs 序中的第 $i$ 个点。对于每一层的节点，将它们按这个 dfs 序从左至右排序，然后在相邻的节点之间连接长为 $1$ 的边。给出 $Q$ 次询问 $(x,y)$，每次询问你需要返回 $x$ 到 $y$ 的最短路长度。

输入格式

第一行两个整数 $n,Q$，分别表示根系的节点数和询问次数。

接下来一行 $n-1$ 个整数 $f_i$，分别表示节点 $i = 2,3,\ldots,n$ 在将根系视作树中的父亲。对于同一层的节点，编号越小意味着在地下的位置越靠左。

接下来 $Q$ 行每行两个整数 $x,y$ ，表示询问。

输出格式

$Q$ 行，每行一个整数表示对应询问的答案。

样例一

input

6 6
1 2 2 2 1 
3 2
1 6
1 5
4 1
5 4
2 4

output

1
1
2
2
1
1

样例二

input

16 10
1 2 1 4 5 1 7 8 8 7 11 7 13 13 13 
2 3
3 5
8 12
2 12
16 10
7 16
10 1
2 10
2 2
14 14

output

1
1
2
4
4
2
3
4
0
0

样例三

input

35 20
1 2 3 2 1 6 7 8 8 7 11 12 7 1 15 16 17 16 19 19 21 21 19 24 25 24 27 27 29 29 31 27 27 34 
11 30
34 4
18 12
24 6
34 3
25 8
26 9
14 14
17 32
32 16
12 19
5 2
34 30
19 26
29 18
32 19
25 20
27 25
1 26
34 20

output

7
7
1
4
7
5
7
0
6
6
3
1
3
3
5
5
3
1
6
4

样例四

见附件下载。

数据范围与提示

对于所有数据，$1\le n,Q\le 10^5$, $1 \le f_i < i$, $1\le x,y\le n$。

时间限制：$5\texttt{s}$

空间限制：$512\texttt{MB}$