之前 rushcheyo 哥哥稍微修了一下题解的格式，所以公开的有点晚了，非常抱歉。

之前有人问我为啥出题人只有一个人，其实是因为出题人的确只有 command_block 一个人。六道题都是他一个人出的造的（虽然 D 题后来发生了一些事故，管理员们改了一波重造了题），非常感谢他愿意来 UOJ 举办这场比赛。

以及 Goodbye Gengzi 现在还缺题，欢迎各位小伙伴来投题啊～

多线程计算

from command_block，标程、数据 by command_block，题解 by rushcheyo

整个过程中一共会产生 $n\times m$ 个随机数，我们将所有的亮起操作按时间排序，就能得到亮灯顺序的排列。由概率论的常识知道，我们可以假设这些数两两不等，且每种排列出现的概率均为 $\frac{1}{(nm)!}$。

• 定理：$[0,1)$ 内的 $n$ 个随机数中第 $k$ 大的数的期望为 $\frac{k}{n+1}$。

  证明可以在很多地方找到。

一个有 $k$ 个处理器亮起的状态，持续时间为第 $k+1$ 大的随机数减去第 $k$ 大的，那么其期望持续时间便为 $\frac{1}{nm+1}$。一个亮灯排列会产生 $nm+1$ 种状态，那么问题转化为统计各个状态的贡献和，最后乘上 $\frac{1}{(nm+1)(nm)!}$ 。

算法一

暴力枚举亮灯排列，然后模拟亮灯过程即可。

复杂度 $O((nm)!nm)$ ，期望得分：$25$。

算法二

由于对称性，一个节能态的贡献只与其亮起的处理器数 $k$ 有关，也就是 $F_kk!(nm-k)!$。下面就只要对所有 $0 \le k \le nm$，算出亮起数为 $k$ 的节能态数量。

由于不同的节能态是独立的，不妨考虑 $h=1$，即计算有恰 $x$ 行 $y$ 列完整亮灯的状态的贡献。考虑容斥原理，我们枚举并强制有 $i$ 行和 $j$ 列是完整亮灯的，除了这些格子外剩下的格子都能任选。那么 $\forall im+jn-ij \le k \le nm$，亮起数为 $k$ 的节能态数量获得了 $\binom n i \binom m j \binom {i} {x} \binom{j}{y} (-1)^{i-x} (-1)^{j-y} \binom{(n-i)(m-j)}{k-im-jn+ij}$ 的贡献。

于是我们获得了一个多项式时间的做法！期望得分：$35$。

算法三

可以发现上面的计算实际上分为两步：先固定下 $im+jn-ij$ 个必亮的格子，再在剩下的 $(n-i)(m-j)$ 个格子中进行任选。我们记录数组 $f_{0..nm},g_{0..nm}$，先对每个 $(x,y)$ 枚举 $i,j$ 将 $\binom n i \binom m j \binom {i} {x} \binom{j}{y} (-1)^{i-x} (-1)^{j-y}$ 累加到 $f_{im+jn-ij}$ 上，再枚举 $p,q$，将 $f_p\binom{nm-p}{q}$ 累加到 $g_{p+q}$ 上，那么最后 $g_{k}$ 就是亮起数为 $k$ 的节能态数量。

复杂度 $O\left(n^2m^2\right)$，期望得分：45。

算法四

将组合数用 $\binom i j = \frac{i!}{j!(i-j)!}$ 拆开，不难发现上面算法的两步分别是二维卷积和一维卷积，那么使用二维 FFT 就可以做到 $O(nm \log nm)$，期望得分 100。

二维 FFT 太高级了我不会怎么办！实际上第一部分的两维是独立的。具体的，我们记录数组 $h_{0..n,0..m}$，先对每个 $(x,y)$ 枚举 $i$ 将 $\binom n i \binom i x (-1)^{i-x}$ 累加到 $h_{i,y}$ 上，结束后再枚举 $j$ 将 $h_{i,y}\binom m j \binom j y (-1)^{j-y}$ 累加到 $f_{im+jn-ij}$ 上，这样只需要 $n$ 次大小为 $m$ 和 $m$ 次大小为 $n$ 的一维 FFT 就可以解决问题了！复杂度不变，期望得分 100。

算法五

from EntropyIncreaser

第二步其实是可以线性时间解决的。

只需解决代价为 $t^k$ 的情况，即可解决斐波那契数。

表示为积分 $$ f_k= \int_0^1(tx)^k(tx+(1-x))^{n-k}\,\mathrm{d}x $$

由 Beta 积分展开： $$ \begin{aligned} f_k &= \int_0^1\sum_j \binom{n-k}j (tx)^{k+j}(1-x)^{n-k-j}\,\mathrm{d}x\\ &= \sum_j \binom{n-k}j t^{k+j}\int_0^1 x^{k+j}(1-x)^{n-k-j}\,\mathrm{d}x\\ &= \sum_j \binom{n-k}j t^{k+j} \frac{(k+j)!(n-k-j)!}{(n+1)!}\\ &= \sum_{j {\color{red}{\le n-k}}} t^{k+j} \frac{(n-k)!}{j!\color{blue}{(n-k-j)!}} \frac{(k+j)!\color{blue}{(n-k-j)!}}{(n+1)!}\\ &= \sum_{j\le n-k} t^{k+j} \frac{(k+j)!}{j!\color{blue}{k!}} \frac{(n-k)!\color{blue}{k!}}{(n+1)!}\\ &= \frac{(n-k)!k!}{(n+1)!}\sum_{j\le n-k} t^{k+j}\binom{k+j}k \\ &= \frac{(n-k)!k!}{(n+1)!}[x^k]\sum_{j\le n-k} t^{k+j} (1+x)^{k+j} \\ &= \frac{(n-k)!k!}{(n+1)!}[x^k]\sum_{j\le n} (t(1+x))^j \\ &= \frac{(n-k)!k!}{(n+1)!}[x^k]\frac{(t(1+x))^{n+1}-1}{t(1+x)-1} \\ \end{aligned} $$

光伏元件

from command_block，数据、标程、题解 by command_block

算法一

暴力枚举所有可能的放置方案。

复杂度 $O(2^{n^2}n^2)$ ，期望得分：$20$。

算法二

解决保证 $k=0$ 且 $C\leq 0$ 的子问题。

这里要求第 $i$ 行和第 $i$ 列的元件数恰好相等，且不在乎费用，只需要任意一种合法方案即可。

考虑使用带有上下界的网络流来求解。

把行和列分别用点表示，对于位置 $(i,j)$ ，从行 $i$ 向列 $j$ 连边。

• 一定为空：不连边。

• 一定有元件 ：$i\rightarrow j$ ，流量 $[1,1]$。

• 可以改变，且初始时为空位：$i\rightarrow j$ 容量 $[0,1]$。

• 可以改变，且初始时为元件：$i\rightarrow j$ 容量 $[1,1]$ ; $j\rightarrow i$ 连边容量 $[0,1]$，表示退流。

如何限制行和列的流量相同呢？

可以发现，行的流量是流出的，列的流量是流入的，可以使用循环流的思路来限制，让列 $i$ 的流量流回行 $i$，如下图：

求循环可行流即可。结合算法一，期望得分 $30$ 分。

算法三

解决保证 $k=0$ 的子问题。

此时要考虑费用的限制，使用最小费用循环可行流。

• 一定为空 : 不连边。

• 一定为元件 : $i\rightarrow j$ ,流量 $[1，1]$，费用为 $0$。

• 可以改变，且初始时为空位 : $i\rightarrow j$ 连边容量 $[0,1]$ ,费用为 $C_{i,j}$。

• 可以改变，且初始时为元件 :

  $i\rightarrow j$ 连边容量 $[1,1]$ ,费用为 $0$。

  $j\rightarrow i$ 连边容量 $[0,1]$，费用为 $C_{i,j}$ ，表示退流。

图中可能有负环，实现时需要使用一些技巧。

结合算法一，期望得分：$50$。

算法四

解决原问题。

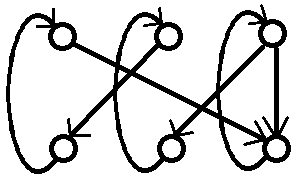
把中间的“反向”边改成这样的设计。

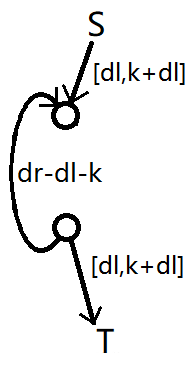
不难发现，由于上下边的下界均为 $dl$ ，能保证各自至少有 $dl$ 的流量。

只需证明 $dl=0$ 的情况。如图:

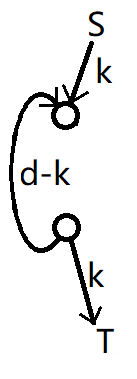
假设上方的流量为 $l$ ，下方为 $r$ ，中间为 $t$。

那么上点的流量为 $l+t$ ，下点的流量为 $r+t$。

显然 $l,r$ 的差不会超过 $k$ ，且 $l+t,r+t\leq d$。

反过来，若给出一组合法的点流量 $a,b$ ，我们让中间的边流 $\min(d-k,a,b)$。

若 $\min(a,b)\geq d-k$ ，则中间的边流了 $d-k$ 。

由于 $a,b\leq d$ ，余下的流量 $a-(d-k)$ 和 $b-(d-k)$ 均 $\leq k$ ，能够被两侧的边装下。

若 $\min(a,b)\lt d-k$ ，不妨设 $a\lt b$ ，则中间的边流了 $\min(a,b)=a$ 。

余下流量为 $0,b-a$ ，由前提约束有 $b-a\leq k$。

期望得分：$100$。

关于费用流的实现

本题的费用流建图点数为 $O(n)$，边数为 $O(n^2)$ ，流量总量为 $O(n^2)$，实际拆出的点数从 $200\sim 400$ 不等。

若采用一般的 Edmonds-Karp 费用流，复杂度瓶颈为 $O(n^2)$ 次增广，这里使用 SPFA 的话复杂度上界为 $O(n^2*nm)=O(n^5)$。如果用 Dijkstra 费用流复杂度降为 $O(n^4)$，然而出题人并不会在本题卡 SPFA，所以还是把较好的实现放过去了。

服务器调度

from command_block，数据、标程、题解 by command_block

算法一

我会暴力！期望得分：$10$。

算法二

不难发现，修改时只会影响 $O(1)$ 种颜色的贡献，只要做到 $O(n)$ 重新计算某种颜色的贡献即可。熟知一个点到一个点集的最远点一定是任意一条直径的某一端点，那么先求出点集直径，然后随便暴力即可。

复杂度 $O(n(n+q))$ ，期望得分：$25$。

算法三

解决无修改的子问题。

先求出每组点集的直径，那么对于一条直径 $(r,b)$ ，整棵树被划分成了两个区域：

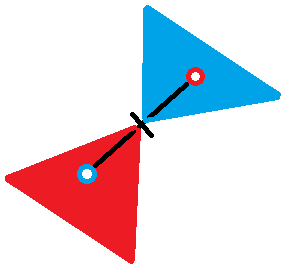
上图中，红色端点是 $r$ ，蓝点是 $b$ ，黑色线是直径，那么红色区域表示距红点更远，蓝色区域则距蓝点更远。

现在，我们要给红色区域的每个点加上到蓝点的距离，给蓝色区域加上到红点的距离。

观察树上两点距离公式：$dis(u,v)=dep(u)+dep(v)-2dep[lca(u,v)]$：对于每个 $u$ ，每个组别都恰好有一个点成为其最远点，那么 $dep[u]$ 就被算入了 $m$ 次，剩下只需计算 $dep[v]-2dep[lca(u,v)]$。

不难发现，两个区域的分界边，就在直径的带权中点处，设其为 $(t_r,t_b)$。不妨设红色区域是 $t_r$ 的子树。

红色区域的点 $u$ 贡献为：$dep[r]-2dep[lca(u,r)]=-dep[r]$ ，只需实现子树减即可。

蓝色区域就不是一颗完整的子树了，点 $u$ 的贡献 $dis(u,b)=dep[b]-2*dep[lca(u,b)]$，分别处理两项，先给每个点加上 $dep[b]$。

如果在 $t_b$ 到根的链上给每个点加上父边的长度，那么从 $u$ 到根求和，则会得到 $dep[lca(u,t_b)]$。然后还需要给 $t_r$ 的子树加上 $2*dep[t_b]$ 抵消贡献。

上述操作都可以用树上差分来解决，注意要特判某种区域只有一个点的情况。

复杂度 $O(n\log n)$，结合算法二，期望得分：$40$。

算法四

解决总是询问所有点延时总和的子问题。

考虑如何动态维护直径，众所周知点集直径是可以合并的，那么可以对每种颜色分别开一棵线段树来维护。为了降低时间，下面需要用到询问 $O(1)$ 的 LCA。

对于每条点集直径，记录下其对答案的贡献，若发生变化重新计算即可，一次修改只会重新计算 $O(1)$ 条直径。

现在，我们只需要计算每条直径对整棵树的贡献：

1. 子树加，只需要预处理子树大小。

2. 在 $t_b$ 到根的链上给每个点加上父边的长度，再让每个点加上自己到根的和。

设 $len_v$ 为 $v$ 的父边长度，$size_v$ 为 $v$ 的子树大小。

考虑 $t_b$ 到根的链上 $v$ 点产生的贡献，会有 $siz_v$ 个点向上求和到 $v$ ，产生 $len_v$ 的贡献，总和即为 $size_v \times len_v$，对这个做树上前缀和即可。

结合算法二，期望得分：$50$；再结合算法三，期望得分：$65$。

算法五

解决原问题。

在上面提及的两种贡献中，子树加使用下标为 dfs 序线段树即可处理，重点在第二类贡献难以计算。考虑一个子树的第二类贡献，如图 :

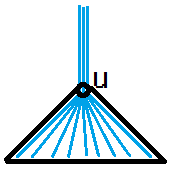
伸出框外的是 $size_u$ 条同样的 $u$ 到根的路径，这部分只需要路径求和即可。框内的贡献为 $u$ 子树内到 $u$ 路径的求和，设其为 $g_u$。

考虑如何求出 $g_u$，不难发现 $u$ 内的某点 $v$ 贡献系数为 $size_v \times len_v$，那么子树求和即可。

复杂度 $ O(n\log^2n)\sim O(n \log n)$，取决于你采用的树上数据结构。期望得分：$100$。

打击复读

from command_block，数据 by skip2004，标程、题解 by mayaohua。

算法一

我会暴力枚举！

直接计算出每个本质不同子串的复读程度，这里可能需要字符串哈希。

修改操作只会修改 $wl_u$ ，那么只会影响到所有以 $u$ 为左端点的子串，容易 $O(n)$ 重新计算。

时间复杂度为 $O(n(n+m))$ ，可以通过 subtask 1，期望得分：$10$。

对于 subtask 2 来说，由于数据随机，所以期望长度 $O(\log n)$ 以上的子串两两不同，直接对长度小于一个阈值 $B=\Theta(\log n)$ 的子串哈希即可。

时间复杂度为 $O(n\log n)$ ，可以额外通过 subtask 2，期望得分：$30$。

算法二

我会后缀树/后缀自动机！

显然若两个子串相同，它们的 $v_l$ 和 $v_r$ 都是相同的。

用 SAM​ 建出反串后缀树，然后尝试统计答案。

考虑反串后缀树上的节点 $x>1$ ，设 $s$ 为 $w$ 的前缀和，$x$代表的子串长度区间为 $[L_x,R_x]$ ，枚举串长 $k$，可得对复读程度贡献为: $$ \begin{aligned} \sum\limits_{k=L_x-1}^{R_x-1}\left(\sum\limits_{t\in right_x}w_{t-k}\right)\left(\sum\limits_{t\in right_x}w_t\right)&=\left(\sum\limits_{t\in right_x}w_t\right)\left(\sum\limits_{t\in right_x}\sum\limits_{k=L_x-1}^{R_x-1}w_{t-k}\right)\\ &=\left(\sum\limits_{t\in right_x}w_t\right)\left(\sum\limits_{t\in right_x}s_{t-L_x+1}-s_{t-R_x}\right)\\ \end{aligned} $$ 可以暴力枚举 $right_x$ 中的元素 $O(\lvert right_x \rvert)$ 计算。注意同一个子串出现了 $\lvert right_x \rvert$ 次，贡献要乘上 $\lvert right_x \rvert$ 。

在数据随机的情况下， $\sum\limits_{x}\lvert right_x \rvert$ 大概是 $O(n\log n)$ 级别的，但在构造的数据下可以卡到 $O\left(n^2\right)$ 级别。

结合算法一可以通过 subtask 1~2，期望得分 $30$ 分。

算法三

我会分块 FFT！

上面计算的式子里面， $\sum\limits_{t\in right_x}w_t$ 是容易计算的，后半部分可以拆开成分别计算 $\sum\limits_{t\in right_x}s_{t-L_x+1}$ 和 $\sum\limits_{t\in right_x}s_{t-R_x}$。下面只以计算后面一个为例。

我们考虑到 $right_x$ 是 $x$ 在反串后缀树中子树里后缀节点的集合。那么考虑对后缀节点做一个树分块，使得每个块大小不超过阈值 $B$ ，对于某个后缀节点 $y$ ，它会出现在它到根的路径上的点 $right$ 集合中，于是我们可以在计算它到块根节点上的点的贡献时暴力枚举它。对于再往上的点 $x$，考虑对同一个块做一次减法卷积，可以一并计算对于这部分 $x$ 的贡献。具体来说，令块中后缀节点集合为 $BL$ ，我们只需要对所有的 $R_x=i \in[1,n]$ ，算出 $f_i=\sum\limits_{y\in BL} s_{y-i}$ ，这显然是一个减法卷积的形式，可以用 FFT 加速。

时间复杂度为 $O\left(nB+\frac{n^2\log n}{B}\right)$ ， 取块大小 $B=\Theta\left(\sqrt{n\log n}\right)$ 可以取到最优复杂度 $O\left(n\sqrt{n\log n}\right)$。

对于 subtask 3，由于 $w_i\leq 10^5$ ，答案总大小不会太大，使用 double 做复数域 FFT 即可。但对于 subtask 4，由于权值可以很大，如果用分块 FFT 可能需要三模数 NTT ，常数非常大，应该是难以通过的，当然你卡常卡过去了当我没说。

结合算法一可以通过 subtask 1~3，期望得分 $60$ 分。

算法四

from command_block

我不会分块 FFT，但我会分析性质！

考虑分析一下 $right$ 集合的分布。

引理：对于串 $S$ ，若 $S$ 相邻三个出现位置右端点 $u,v,w$ 满足 $u\lt v\lt w$ ，且 $w-u\leq \lvert S \rvert$ ，那么一定有 $v-u=w-v$ ，也就是 $u,v,w$ 形成等差数列。

这个是 the periodicity lemma 的直接推论。

那么我们考虑对原串分块。取一个块大小 $B$ ，然后对于一个节点 $x$ ，若 $R_x\leq B$ ，我们仍然用算法二计算。若 $R_x>B$ ，那么由引理，它在同一个块内 $right$ 集合的分布一定是一个公差 $\leq B$ 的等差数列，只需要记录最左和最右以及个数就可以确定公差了。于是我们要求的 $\sum\limits_{t\in right_x}s_{t-R_x}$ 中， $t-R_x$ 也是一个公差相同的等差数列，那么我们 $O(nB)$ 预处理出所有公差的等差数列前缀和，即可单个块单次 $O(1)$ 求和。

这样总复杂度为 $O\left(nB+\frac{n^2}{B}\right)$ ，取块大小 $B=\Theta(\sqrt n)$ 可以取到最优复杂度 $O\left(n\sqrt n\right)$ 。

直接实现空间复杂度也是 $O\left(n\sqrt n\right)$ 的（也可以优化到 $O(n)$ ），不过通过subtask4还是没问题的。结合算法一可以通过 subtask 1~4，期望得分 $80$ 分。

算法五

from ezoilearner

$O(n\sqrt n)$ 是极限了吗？

扔掉分块的想法，重新考虑我们要计算的东西： $\sum\limits_{t\in right_x}s_{t-R_x}$ 。可以注意到一个重要的事情：对于所有的 $t\in right_x$，$S[t-R_x+1,t]$ 是 $x$ 代表的子串中的一个，因此它们都是相同的。

那么我们考虑直接重新建出正串的后缀树（相当于建出反串的 SAM），在上面定位出 $S[t-R_x+1,t]$ 的对应节点 $y$ ，那么 $\sum\limits_{t\in right_x}s_{t-R_x}$ 即为 $\sum\limits_{t'\in right_y}s_{t'-1}$ ，这容易预处理出来。那么现在的问题就变成给出 $O(n)$ 个子串，在后缀树上定位它们，直接实现可以考虑倍增做到 $O(n\log n)$ ，也可以离线下来用并查集做到 $O(n\alpha(n))$ 甚至 $O(n)$ 。

如果我们要支持修改，这也是简单的：

我们先将整个串翻转，后面可以认为是修改右权值 $wr_u$ 。那么我们若对于每个 $1\leq i\leq n$ 都预处理出 $f_i=\sum\limits_{j=1}^{i}vl(s[j,i])$ ，那么容易 $O(1)$ 修改。

而考虑算法五的过程，对于每个节点 $x$ 和 $t\in right_x$ ，我们事实上计算出了 $\sum\limits_{i=L_x}^{R_x}vl(s[t-i,t])$ ，显然只需要对每个 $i$ ，把它到根路径上节点的贡献加起来，就得到了要求的 $f_i$ 了。

那么时间复杂度即为 $O(n+m)\sim O(n\log n+m)$ 。可以通过 subtask 1~5 ，期望得分 $100$ 分。

算法六

from matthew99, skip2004 and mayaohua

这里有另外一个角度：我们不从后缀树的角度，而是从自动机的角度考虑。

为了方便讨论，我们不翻转字符串，还是修改左权值 $wl_u$ ，同样变为对于每个 $1\leq i\leq n$ 预处理出 $f_i=\sum\limits_{j=i}^{n}vr(s[i,j])$ 。

然后我们考虑直接建出正串的 SAM ，这是一个 DAG 。按照 SAM 自身的性质，我们如果固定左端点 $i$ ，那么只要依次在 SAM 上匹配子串 $s[i,n]$，得到一条从根节点出发的路径，就可以依次得到子串 $s[i,j](i\leq j\leq n)$ 在正串 SAM（反串后缀树）上所在的节点，而对于同一个节点 $x$ ，它所表示的每个子串的 $vr$ 和出现次数都是定值，将它们的乘积称为 $g_x$ ， $g_x$ 容易预处理出。这样，我们只需要依次把路径上所有节点的 $g_x$ 求和，显然就是 $f_i$ 了。

这是一个 DAG 上路径求和的问题，看起来很不可做？

利用一下 SAM 自身的特殊性质：这是一个 $O(n)$ 个点， $O(n)$ 条边的 ​DAG，且从根结点出发，能走出的不同路径数目即为原串的不同子串个数，为 $O\left(n^2\right)$ 级别。对于这一类从根节点出发的不同路径数目不太大的 DAG ，直观上它的结构应当与一棵有根树类似。对于有根树，一个经典的处理技巧是重链剖分，而这在这类 DAG 上面也是成立的。以 SAM 为例，若我们只保留所有的转移边 $(u,v)$ ，满足到达 $u$ 的路径数目大于到达 $v$ 的路径数目一半，且从 $v$ 出发的路径数目大于从 $u$ 出发的路径数目一半，这样剩余的子图显然会形成若干条链，且每个点恰好在一条链上。这样，我们容易证明，从根结点出发的任何一条路径，至多经过 $O(\log n)$ 条不在链上的转移边（也意味着至多经过 $O(\log n)$ 条链） 。

有了这个结构，我们做这个问题就很简单了：类似树上的重链剖分，每次从根节点开始，跳链求和即可。对于不在链上的转移边，我们可以直接知道走哪条，但在一条链上我们需要知道走多少条边，可以发现这只需要知道当前的 $s[j,n]$ 后缀与链末尾节点代表的子串的 LCP，即可立刻得到。这容易用后缀数组和 ST 表做到 预处理 $O(n\log n)$，单次查询 $O(1)$。

那么，总时间复杂度即为 $O(n\log n+m)$ ，期望得分 $100$ 分，这里是一份提交记录。

值得一提的是，如果用算法七的角度来看，算法六其实就是对正串后缀树进行了重链剖分，这显然是多此一举的。至少在这个问题上， DAG 剖分的思想并没有带来更优秀的复杂度。

算法七

from mayaohua

如果把算法五的正反串对应思想，和算法六的自动机结合起来，能得到什么呢？

我们考虑分别建出正串 SAM （反串后缀树） 和正串后缀树（反串 SAM）。

考虑原串的每个子串，它在正串 SAM 上对应一个节点，在正串后缀树上对应另一个节点。那么考虑正串后缀树上的某个节点 $x$ ，它对应的子串长度为 $[L_x,R_x]$ ，令 $right_x$ 中某个元素为 $t$ ，则它们分别为 $s[t,t+L_x]\sim s[t,t+R_x]$ 。令子串 $s[l,r]$ 在正串 SAM 上对应节点为 $node(s[l,r])$ 。

引理：对 $L_x\leq i\lt R_x$ ， $node(s[t,t+i])$ 恰有一条出边，且指向 $node(s[t,t+i+1])$ 。且当 $x$ 不是一个后缀节点，也即 $s[t,t+R_x]$ 不是一个原串后缀时， $node(s[t,t+R_x])$ 至少有两条出边。

证明：显然 $node(s[t,t+i])$ 会有一条指到 $node(s[t,t+i+1])$ 的边，且若存在至少两条出边，那么意味着 $s[t,t+i]$ 存在至少两个不同的后继字符，因此不可能与 $s[t,t+i+1]$ 在同一条边上。同时若 $s[t,t+R_x]$ 不是原串后缀时，意味着 $x$ 至少有两个儿子，也即有至少两个不同的后继字符，因此 $node(s[t,t+R_x])$ 至少有两条出边。

这给出了一个非常简单的算法：同算法六一样考虑计算 $f_i$ ，我们考虑直接在正串后缀树上 DFS ，设现在到了正串后缀树的节点 $x$ ，在正串 SAM 上对应节点 $y$ 以及当前的总和。那么我们考虑对 $x$ 的某个节点 $u$ ，我们希望得到 $u$ 对应子串的 $vr$ 的和，在总和中加上它与 $\lvert right_u \rvert$ 乘积得到新的总和，则 DFS 到后缀 $s[i,n]$ 对应节点时的总和即为 $f_i$ 。那么直观的方式是从 $y$ 开始在正串 SAM 上不断经过边上的字符串得到一条路径并对路径上节点的 $vr$ 求和。根据我们上面的引理，若我们 $O(n)$ 预处理出从每个 $y$ 出发，不断走到后继点，直到至少有两个后继或是到达后缀节点时所走到的点 $next_y$ 以及路径上的点的 $vr$ 和 $sum_y$ ，那么每次就是走到 $next_y$ ，且所求的和就是 $sum_y$ 。

这样就得到了一个非常简单的 $O(n+m)$ 算法，期望得分 $100$ 分，这里是一份提交记录。

这个算法的扩展性非常强，修改贡献函数或是支持对单侧权值的复杂修改都不是问题（可能需要结合一些正串后缀树上的处理算法）。我们在 DFS 的过程中，其实就是在每个节点处找到了算法五中所求的在另一边后缀树上的定位，但这里不需要差分，因此即使贡献函数不可减，也能非常完美的解决。

同时，这里我们事实上把正串 SAM 上非后缀节点，且出度为 $1$ 的点缩了起来，这个结构就是徐翊轩的集训队论文《浅谈压缩后缀自动机》中的“压缩后缀自动机”，更进一步的分析可以阅读论文，这里就不展开了。

校验码

from command_block，数据、标程、题解 by command_block

为了方便，下文默认 $c$ 为给定参数，将 $q(n,c)$ 简写为 $q(n)$。

算法一

使用筛法求出 $nm$ 以内的 $q$ 函数值，然后暴力计算和式。

复杂度 $O(nm)$ 或 $O(nm\log nm)$，期望得分：$10$。

算法二

解决 $n=1$ 时的子问题。

熟练的选手会使用各种筛法或 powerful numbers 完成本部分分。与正解无关故不展开介绍。

• 观察：$q(d^2n)=d^c*q(n)$

现求 $\sum_{i=1}^m q(i)$，令 $i=d^2t$ ，且 $t$ 不含平方因子，我们枚举 $d,t$ 来代替 $i$，得到： $$ \begin{align*} &\sum_{t=1}^m\mu^2(t)\sum_{td^2\leq m}q(d^2t)\\ =&\sum_{t=1}^m\mu^2(t)\sum_{td^2\leq m}d^cq(t)\\ =&\sum_{t=1}^m\mu^2(t)\sum_{td^2\leq m}d^c \end{align*} $$

• 设 $S_1(n)=\sum\limits_{i=1}^ni^c$ , 则 $\sum\limits_{td^2\leq n}d^c=\sum\limits_{i=1}^{\left\lfloor \sqrt{m/t}\right\rfloor}i^c=S_1\big(\big\lfloor \sqrt{m/t}\big\rfloor\big)$

由于涉及到的 $S_1$ 的求和上界不超过 $\sqrt{m}$ ，线性筛预处理即可，复杂度 $O(\sqrt{m})$。

现在答案是 $\sum\limits_{t=1}^m\mu^2(t)S_1\left(\left\lfloor \sqrt{m/t}\right\rfloor\right)$。

对 $\left\lfloor \sqrt{m/t}\right\rfloor$ 整除分块：

当 $t\leq m^{1/3}$ 时，显然不超过 $m^{1/3}$ 段。

当 $t>m^{1/3}$ 时，则有 $\sqrt{m/t}\leq m^{1/3}$ ，即不同的值不超过 $m^{1/3}$ 种。

那么每段只需要求 $\mu^2$ 的前缀和，由容斥原理知道：

$$\sum\limits_{i=1}^n\mu^2(i)=\sum\limits_{i=1}^{\sqrt{n}}\mu(i)\left\lfloor n/i^2\right\rfloor$$

那么 $\left\lfloor n/i^2\right\rfloor$ 同样会形成 $O(n^{1/3})$ 段，整除分块计算即可。

这部分复杂度 $O\left(\sum\limits_{k=1}^{m^{1/3}}\left(m/k^2\right)^{1/3}\right)=O(m^{4/9})$，总复杂度 $O(\sqrt{m})$，期望得分：$25$，结合算法一可得 $35$ 分。

算法三

同样考虑提取 $i,j$ 中的平方因子，表示成两对二元组 $(d_1,t_1),(d_2,t_2)$。 $$ \begin{align*} &\sum\limits_{i=1}^n\sum\limits_{j=1}^mq(ij)\\=&\sum\limits_{t_1=1}^n\mu^2(t_1)\sum\limits_{t_1d_1^2\leq n}\sum\limits_{t_2=1}^m\mu^2(t_2)\sum\limits_{t_2d_2^2\leq m}q(t_1d_1^2t_2d_2^2)\\=&\sum\limits_{t_1=1}^n\mu^2(t_1)\sum\limits_{t_1d_1^2\leq n}\sum\limits_{t_2=1}^m\mu^2(t_2)\sum\limits_{t_2d_2^2\leq m}d_1^cd_2^cq(t_1t_2)\\=&\sum\limits_{t_1=1}^n\mu^2(t_1)S_1\left(\left\lfloor \sqrt{n/t_1}\right\rfloor\right)\sum\limits_{t_2=1}^m\mu^2(t_2)S_1\left(\left\lfloor \sqrt{n/t_2}\right\rfloor\right)\gcd(t_1,t_2)^c\\=&\sum\limits_{t_1=1}^n\mu^2(t_1)\left(\sum\limits_{t_1d_1^2\leq n}d_1^c\right)\sum\limits_{t_2=1}^m\mu^2(t_2)\left(\sum\limits_{t_2d_2^2\leq m}d_2^c\right)q(t_1t_2)\\=&\sum\limits_{t_1=1}^n\mu^2(t_1)S_1\left(\left\lfloor \sqrt{n/t_1}\right\rfloor\right)\sum\limits_{t_2=1}^m\mu^2(t_2)S_1\left(\left\lfloor \sqrt{n/t_2}\right\rfloor\right)q(t_1t_2)\\=&\sum\limits_{t_1=1}^n\mu^2(t_1)S_1\left(\left\lfloor \sqrt{n/t_1}\right\rfloor\right)\sum\limits_{t_2=1}^m\mu^2(t_2)S_1\left(\left\lfloor \sqrt{n/t_2}\right\rfloor\right)\gcd(t_1,t_2)^c \end{align*} $$ 最后一步是因为 $t_1,t_2$ 质因子次数都是 1。

令 $f=\mu*id_c$（此处不是复杂度瓶颈，可以暴力计算），然后我们就可以用 $f$ 来反演掉 $\gcd^c$：

$$ \begin{align*} &\sum\limits_{t_1=1}^n\mu^2(t_1)S_1\left(\left\lfloor \sqrt{n/t_1}\right\rfloor\right)\sum\limits_{t_2=1}^m\mu^2(t_2)S_1\left(\left\lfloor \sqrt{n/t_2}\right\rfloor\right)\gcd(t_1,t_2)^c\\=&\sum\limits_{t_1=1}^n\mu^2(t_1)S_1\left(\left\lfloor \sqrt{n/t_1}\right\rfloor\right)\sum\limits_{t_2=1}^m\mu^2(t_2)S_1\left(\left\lfloor \sqrt{n/t_2}\right\rfloor\right)\sum_{r|t_1,r|t_2}f(r)\\=&\sum_r f(r) \sum_{t_1=1}^{n/r} \mu^2(t_1r)S_1\left(\left\lfloor\sqrt{n/(t_1r)}\right\rfloor\right) \sum_{t_2=1}^{m/r} \mu^2(t_2r)S_1\left(\left\lfloor\sqrt{n/(t_2r)}\right\rfloor\right) \end{align*} $$ 现在分成了两个独立的部分。

设 $S_2(n,d)=\sum\limits_{i=1}^{n}\mu^2(id)S_1\left(\left\lfloor \sqrt{n/i}\right\rfloor\right)$，现在问题变为了求若干个 $S_2$。

为了避免混淆，下面一律用 $N,M$ 代替题面中的 $n,m$。

考虑常见问题：对于一个数论函数 $f$，当给定 $N$ 时，对所有的 $k=\lfloor N/i\rfloor$ 求出 $\sum_{i=1}^kf(i)$。

• $\mu^2$：预处理到 $L$ ，其余部分整除分块，复杂度为 $O\left(L+\sum\limits_{i=1}^{M/L}(M/i)^{1/3}\right)=O\left(L+M/L^{2/3}\right)$，取 $L=M^{3/5}$ 可得复杂度为 $O(M^{3/5})$。

• $S_2(n,d)=\sum\limits_{i=1}^{n}\mu^2(id)S_1\big(\big\lfloor \sqrt{n/i}\big\rfloor\big)$

  • 先求出 $d=1$ 时的根号处前缀和。

    考虑预处理至 $L$。先求 $$ \begin{align*} &\Delta S_2(n,1)\\:=&S_2(n,1)-S_2(n-1,1)\\=&\sum\limits_{i=1}^{n}\mu^2(i)S_1\left(\left\lfloor\sqrt{n/i}\right\rfloor\right)-\sum\limits_{i=1}^{n-1}\mu^2(i)S_1\left(\left\lfloor\sqrt{(n-1)/i}\right\rfloor\right)\\=&\sum\limits_{i=1}^{n}\mu^2(i)\left(S_1\left(\left\lfloor\sqrt{n/i}\right\rfloor\right)-S_1\left(\left\lfloor\sqrt{(n-1)/i}\right\rfloor\right)\right) \end{align*} $$ 注意到 $\left\lfloor\sqrt{n/i}\right\rfloor \ne \left\lfloor\sqrt{(n-1)/i}\right\rfloor\Leftrightarrow i|n$ 且 $n/i$ 是完全平方数，而且不相等时，两者总是恰好差 $1$。设 $n/i=d^2$，枚举每个完全平方数的倍数贡献即可。再做前缀和即可得到各个 $S_2(n,1)$ ，复杂度是 $O\Big(\sum\limits_{d=1}^{L}\dfrac{L}{d^2}\Big)=O(L)$。

    其余部分整除分块计算，复杂度为 $O\left(L+\sum\limits_{i=1}^{M/L}(M/i)^{1/3}\right)=O\left(L+M/L^{2/3}\right)$，取 $L=M^{3/5}$ 可得复杂度为 $O(M^{3/5})$。

  • $d>1$ 时递推： $$ \begin{align*} &S_2(n,k)\\=&\sum_{i=1}^n \mu^2(ik) S_1\left(\left\lfloor\sqrt{n/i}\right\rfloor\right)\\=&\mu^2(k)\sum_{i=1}^n \mu^2(i) [i \perp k] S_1\left(\left\lfloor\sqrt{n/i}\right\rfloor\right)\\=&\mu^2(k)\sum_{d|k}\mu(d)\sum_{d|i,1 \le i \le n} \mu^2(i) S_1\left(\left\lfloor\sqrt{n/i}\right\rfloor\right)\\=&\mu^2(k)\sum_{d|k}\mu(d)\sum_{i=1}^{n/d}\mu^2(id)S_1\left(\left\lfloor\sqrt{n/(id)}\right\rfloor\right)\\=&\mu^2(k)\sum_{d|k}\mu(d)S_2\left(\lfloor n/d\rfloor,d\right) \end{align*} $$

对于 $S_2(n,d)$ 中 $nd\leq N$ 的 $O(N\log N)$ 个，我们使用类似的差分技巧预处理，复杂度为 $O(N\log N)$。

我们递推计算其余的 $S_2$，若 $nd\leq N$ 直接返回。

注意到转移中需要枚举约数，由于所有的 $d$ 都没有平方因子，可以对各个素因子压位，这样枚举约数就变成了枚举子集。

$\mu(d)$ 的值也可以根据素因子集合大小的奇偶性得出。

• 粗略的复杂度估界：

  整除起始点为 $M$，对于每个 $d$ ，考虑 $S_2(n,d)$ 中涉及到的 $n$，是由 $M$ 整除若干数得到的。而 $d$ 可能是由某 $kd$ 枚举因数得来，再重复选若干个 $d$ 得到的。

  $\lfloor M/(kd) \rfloor$ 共有 $O(\sqrt{M/d})$ 种取值，当 $d\leq \sqrt{N}$ 时，总状态量为 $O\left(\sum\limits_{d=1}^{\sqrt{N}}\sqrt{M/d}\right)=O(\sqrt{M}N^{1/4})$。

  当 $d>\sqrt{N}$ 时，递归至多进行两层，第二层必须选 $d$ ，所以只有第一层才能选择 $kd$。

  由于 $kd\leq N$，选取 $k$ 的方案数是 $N/d$。总状态量 $O\left(\sum_{d \ge 1} N/d\right)=O(N\log N)$。

  单次转移的复杂度有显然的上界 $2^{w(N)}=64$ ，实际转移复杂度更小。

  于是总时间得到了一个粗略的上界 $O\left(\left(\sqrt{M}N^{1/4}+N\log N\right)2^{w(N)}\right)$。

实际上，当 $N=4\times 10^5,M=1.6\times10^{11}$，且预处理 $nd\leq N$ 以内答案时，对每个 $d$ 做一次不记忆化的递推，转移次数仅为 $6\times 10^6$ 级别。若没有预处理 $nd\leq N$ 以内答案，则转移次数是 $3\times 10^7$ 级别。

除了此部分递推外的时间是 $O\left(M^{3/5}+N \log N\right)$。

期望得分：$100$。

算法四

from rushcheyo

约定 $f(n)$ 为将 $n$ 的素因子幂次全部对 2 取模后得到的数。 $$ \begin{align*} &\sum_{i=1}^n\sum_{j=1}^m q(i)q(j) \left(\gcd\left(f(i),f(j)\right)\right)^c\\=&\sum_{1 \le x \le n,\\\mu(x) \ne 0}x^c\sum_{i=1}^n\sum_{j=1}^mq(i)q(j)\left[\gcd\left(f(i),f(j)\right)=x\right]\\=&\sum_{1 \le x \le n,\\\mu(x) \ne 0} x^c \sum_{x|y,\mu(y)\ne 0} \sum_{x|z,\mu(z) \ne 0} \left[\gcd(y,z)=x\right] \sum_{1 \le i \le n,f(i)=y} q(i) \sum_{1 \le j \le m,f(j)=z} q(j)\\=&\sum_{1 \le x \le n,\mu(x) \ne 0} x^c\sum_{x|y,\mu(y)\ne 0}\sum_{x|z,\mu(z) \ne 0} \sum_{dx|y,dx|z} \mu(d) \sum_{1 \le i \le n,f(i)=y}q(i)\sum_{1 \le j \le m,f(j)=z}q(j)\\=&\sum_{1 \le x' \le n,\mu(x') \ne 0} g(x') f(n,x') f(m,x') \end{align*} $$ 其中：$f(n',x')=\sum_{1 \le i \le n',x'|f(i)} q(i)$，$g(x')=\sum_{d|x'}\mu(d) \cdot \left(\frac {x'}{d}\right)^c$ 可以线性筛预处理出来。而 $f(n,x')$ 可以暴力计算，下面就记 $T(x')=g(x')f(n,x')$。现在： $$ \begin{align*} &\sum_{1 \le x' \le n,\mu(x')\ne 0}f(m,x')T(x')\\=&\sum_{1 \le i \le n,\mu(i) \ne 0} T(i) \sum_{1 \le j \le m,i|f(j)}q(j)\\=&\sum_{1 \le j \le m}q(j)\sum_{i|f(j)}T(i) \end{align*} $$ 我们考虑从小到大枚举 $j$ 的质因子幂次，后面对 $T$ 的求和直接进行暴力，复杂度 $O\left(n \log n+m2^{\omega(m)}\right)$（实际上 $f(j)$ 的平均质因子数量并不多）。可以通过前两个子任务拿到 25 分。

下面我们考虑在枚举的时候避开最大质因子。假如现在枚举到了质数 $p_j$，已经确定的部分为 $x$，我们考虑直接将 $x$ 乘上一个大于 $p_j$ 的质因子得到的数的贡献全部算进答案。这里需要 $\sum_{p \in P} q(xp) \sum_{i|pf(x)} T(i)=q(x) \sum_{p \in P} \sum_{i|pf(x)} T(i)=q(x) \sum_{i} T(i) \sum_{p \in P,i|pf(x)}1$。注意 $p$ 比 $f(x)$ 中所有质数都大。如果 $i$ 的最大质因子为 $p$，那么 $T(i)$ 的贡献为 1。那么这里我们需要对满足 $i$ 的最大质因子大于 $p_j$，$i$ 去掉最大质因子后是 $f(x)$ 约数的 $i$ 求和，直接枚举 $f(x)$ 的约数调用前缀和即可；否则 $i$ 的最大质因子不为 $p$，随便加一个质数就行，这里只需要对 $f(x)$ 的约数上的 $T(i)$ 求和再乘上一个范围内的质数个数就行。于是我们还需要用一个 DP 预处理出所有 $\lfloor m/x \rfloor$ 处的前缀素数个数。

上面这段做法有个名字：Min_25 筛。DP 预处理的部分复杂度是 $O(m^{3/4}/\log m)$，做法随处可见；后半部分的搜索复杂度被证明是 $O\left(m^{1-\varepsilon}\right)$，在本题范围下可以近似为 $O\left(m^{3/4}2^{\omega(m)}/\log m\right)$。对此种做法的详细分析见朱震霆 2018 年中国国家候选队论文《一些特殊的数论函数求和问题》。期望得分：65~80。

算法五

from ilnil

见 https://ilnil.blog.uoj.ac/blog/6538 。

卫星基站建设

from command_block，数据、标程、题解 by command_block

为了避免细节，我们给所有的点加上随机扰动，那么就不会出现三点共线，三线交于一点等等情况了。

算法一

暴力枚举卫星集合 $T_1$ ，求其补集 $T_2$ 。判定 $T_1,T_2$ 的交是否为空。

若两者的交都不为空，则从交区域中分别取一点建立基站。否则必然不可能完整收集。

将能够完整收集的方案中对应的“主星”计入答案。

复杂度 $O\left(2^nn\right)$ ，期望得分 $20$ 分。

算法二

我们发现，卫星集合的个数虽然很多，实际能够连在同一个基站中的却很少。

可以把三角形描述为三个半平面的交集，点在三角形内等价于点同时在三个半平面内。

设集合 $H_p$ 为覆盖点 $p$ 的半平面集合。对于一个确定的 $H_p$ ，显然可以得出对应的 $T_p$。

若 $p_1,p_2$ 的连线没有经过任何一条半平面分界线，则显然有 $H_{p_1}=H_{p_2}$。

$O(n)$ 个半平面分界线会把平面划分成 $O\left(n^2\right)$ 个部分 (如图) ，其中每个部分内的点都满足连线不经过任意的分界线。

于是，只有 $O(n^2)$ 种能够出现的 $H$ 集合。$T$ 集合也只有 $O(n^2)$ 种。

怎么找到这些集合呢?

求出分界线的所有 $O(n^2)$ 个交点(称作关键点)，在每条直线上给这些交点分别排序。

对于相交的两条直线，与交点相邻的有 $4$ 个关键点，组成四个三角形，分别取三角形内部任意一点。如图：

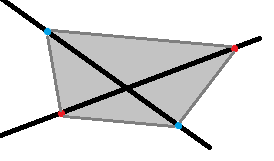
这样能够保证每个区域内至少被取到一个点，正确性较显然。

对于每个点，分别求出它的 $T$ 集合，然后去重。这一部分复杂度是 $O\left(n^3\right)$ 的。

接下来问题可以视作 : 给出一些集合，找出两个集合的并集等于全集。

那么，可以枚举两个集合计算并集，若使用位运算优化，复杂度可视作 $O\left(n^5/\omega\right)$，其中 $\omega$ 为机器位长。

在 $n\leq 50$ 时可以直接使用 unsigned long long 压位。

期望得分 $45$ 分。

算法三

不难发现方案中两个基站的地位是相同的。可以只统计 $p_1$ 对答案的贡献， $p_2$ 只要负责完整收集剩下的卫星。

对于某个 $p_1$ ，求 $T_{p_1}$ 的补集 $S$ ，再求 $S$ 中三角形的交集（半平面交）。

若有交集则表示集合 $T_{p_1}$ 可以贡献。

复杂度为 $O\left(n^3\right)$，期望得分 $60$ 分。

算法四

• 性质 1

  对于平面划分中的一个区域，与其相邻的区域的 $H$ 集合，只有一个半平面的状态不同，可以 $O(1)$ 维护。

  我们可以按照某种顺序依次在相邻的区域之间移动，这样每次只会有最多一个碎片进出当前的 $T$ 集合。

下面利用性质 1来快速求出每个区域的 $T$ 集合。

像沿着墙壁摸一样找出各个区域的边界，如图:

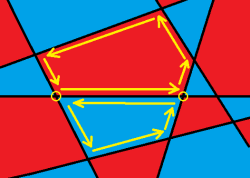
实现细节上，需要记录每个交点是由那条直线产生的，还要记录反映射等等。

建立对偶图，区域用点表示，相邻的区域之间连边，边上记录变化的半平面。

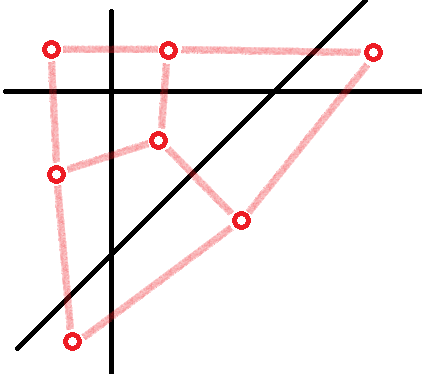
对该图进行遍历即可求出每个区域的 $H$ 集合。

标程使用了堆顺便求出每个点 $T$ 集合的表面碎片，这部分复杂度为 $O(n^2\log n)$。

如果只利用性质 1 ，可以将问题转化成同时带有加入和删除的半平面交问题。

可以采用线段树分治配合数据结构（李超树等）维护，复杂度至少为 $O\left(n^2\log^2n\right)$ 且常数较大，不能承受。

这里有一个剪枝：不被任何三角形覆盖的区域不求解，相邻的 $T$ 集合相同的区域只求解一次。

• 性质 2

  在对偶图中距离某点 $k$ 条边以内的点集大小是 $O\left(k^2 \right)$ 的。

  （粗略的）证明：不妨令起点连通块过原点，一条直线是 $y$ 轴。

  考虑和 $y$ 轴交点坐标最小的 $k$ 条直线。

  任意一个连通块只要包含这 $k$ 条直线每条往右 $k$ 个交点，就是可达的。

  这已经产生了 $O(k^2)$ 个可达的区域。

  实现：一个三角形的进出会导致 $3$ 个半平面的变动。

  无进出的边连接的区域是等价的，不必处理多次，边权也可视为 $0$。

  每次随机选取未被覆盖的一个点，并覆盖周围 $k$ 条边以内的点集。

  复杂度正确性留给读者思考。

考虑选定一个阈值 $k$ ，构造 $O\left(n^2/k^2\right)$ 个关键点来覆盖整张图。

对于每个关键点，进行一定的预处理之后，可以回答距离自己 $k$ 条边内的所有点。

经过的 $k$ 条边，可能存在删除操作。若预处理出 $k$ 层凸壳，每次删边只会破坏一层，足以应付。

在 $k$ 层凸壳中截出的每条线段 $x$ 坐标范围中取一点，收集起来，称之为关键位。显然关键位有 $O(n)$ 个。

预处理时，对于每层凸包，分别对每个关键位记下被哪条直线覆盖，这样可以 $O(1)$ 找到对应直线，无需二分。

这样，预处理一次的复杂度是 $O(nk)$ 的，总预处理复杂度是 $O\left(n^3/k\right)$。

现在我们需要对历经过 $k$ 次修改的凸壳做 $O(\log n)$ 次关键位上的求值。

求值时，若当前层凸壳上对应的直线被删去了，则查找未被删除的前驱后继更新答案，并进入下一层。

对于散着加入的 $k$ 条直线，则暴力计算，也可以先单独建立凸壳然后二分（以减小常数）。

一次求值的复杂度显然是 $O(k)$ 的（严重不满），回答某个询问的复杂度是 $O(k\log n)$ 的，总复杂度是 $O\left(n^2k\log n\right)$。

实现时，可以懒处理，第一次问到某层才预处理该层，可以有效减小常数。

最后，把二分出来的相邻两个关键位求值时牵涉到的直线，和新加入的所有直线求半平面交，看看是否为空即可。

这部分直线是 $O(k)$ 条，复杂度可不计。

取 $k=\Theta\left(\sqrt{n/\log n}\right)$ ，可得复杂度为 $O\left(n^2\sqrt{n\log n}\right)$。

由于数据规模和小常数，本算法表现优异。具体代码实现较为繁琐。

期望得分 $100$ 分。