在大漠中奔波数周修好电站之后，你以迅雷不及掩耳之势在三天内搭好了“跳找”的基本框架。

现在你开始思考“跳找”服务器的部署和联动问题。

“跳找”计划布置 $n$ 个服务器，编号 $1\sim n$。

这 $n$ 个服务器被 $n-1$ 条网络线路连接，即线路形成一个树形结构。树以 $1$ 号服务器为根。

每个服务器 $u$ 都有一个组别 $va{l}_u$，组别有 $m$ 个，分别为 $1\sim m$。

每条网络线路都有一定的延时，定义 $dis(u,v)$ 为服务器 $u,v$ 之间线路延时的和，即树上 $u,v$ 间简单路径的边权和。

定义服务器 $u$ 的延时为 $\sum _{k=1}^m\underset{va{l}_v=k}{max}dis(u,v)$，也即对每个组别的最大延迟求和。

为了测试整个服务器网络的性能，需要完成下列 $q$ 个操作：

• 修改服务器 $u$ 的组别；

• 查询 $u$ 子树内所有服务器的延时总和。

输入格式

第一行一共三个正整数 $n,m,q$，表示服务器个数，组别数以及操作个数。

第二行一行 $n$ 个数，第 $i$ 个数 $va{l}_i$ 表示服务器 $i$ 一开始的组别。

第三行一行 $n-1$ 个数，第 $i$ 个数 ${fa}_{i+1}$ 表示服务器 $i+1$ 的父亲的编号。

第四行一行 $n-1$ 个数，第 $i$ 个数 $le{n}_{i+1}$ 表示服务器 $i+1$ 与父亲之间的边的边长。

下面 $q$ 行，每行开头为一个正整数 $op{t}_i$，表示第 $i$ 次的操作类型：

• 若 $op{t}_i=1$，那么下面紧跟两个整数 $u_i,v_i$，表示将服务器 $u_i$ 的组别修改为 $v_i$；

• 若 $op{t}_i=2$，后跟一个整数 $u_i$，表示查询 $u_i$ 子树内所有服务器的延时总和。

保证一开始及每次操作过后，每个组别都拥有至少一个服务器。

输出格式

对于每个询问，输出一行一个整数，表示该询问的答案。

样例一

input

8 3 6
1 2 3 2 3 2 2 3
1 2 2 1 5 6 4
1 1 1 1 1 1 1
2 1
2 2
1 4 1
2 5
1 7 3
2 2

output

79
40
36
44

explanation

样例一中，每个服务器的延时如图 :

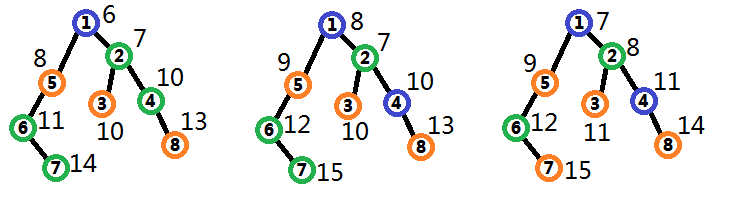
样例二

input

15 4 5
2 1 3 4 1 3 3 4 2 1 2 2 1 3 2
1 1 3 2 2 1 3 4 9 10 4 8 12 10
60 39 99 85 78 41 87 70 19 8 60 60 18 3
2 1
2 2
2 3
2 4
2 5

output

16657
3820
11041
8125
1396

样例三

input

15 4 10
4 2 4 3 2 1 4 1 1 1 2 2 3 3 3 
1 1 3 3 4 2 7 8 7 6 11 9 11 6 
41 43 67 66 77 76 85 90 76 39 20 56 88 100 
1 12 1
2 1
1 7 1
2 1
1 1 1
2 1
1 13 2
2 1
1 4 2
2 1

output

23399
22389
22045
21816
21816

限制与约定

对于所有的数据，保证 $1\le n,q\le 2\times {10}^5,2m\le n,1\le le{n}_i\le 200,1\le f{a}_i<i,1\le u_i\le n,1\le v_i,va{l}_i\le m$。

时间限制：$2\mathtt{\text{s}}$

空间限制：$512\mathtt{\text{MB}}$

下载

样例数据下载