UOJ Σ* Round #1 题解

写在前面

由于第二题原本的题目描述并不对应解法，且原本的题目表述是更为困难的问题，第二题题面应该进行修改。然而，发现这一点时比赛时间已经接近结束（我在复核题解证明的时候发现的错误），因此我们不得不遗憾地宣布，由于这一问题，我们现在对第二题的题目描述进行修改，并且本场比赛将不会计分（unrated）。

最开始的第二题游戏规则是这样的，没有现在这样的多轮操作：

首先艾莉芬在棋盘上放置一些带颜色的积木。然后蔡德仁可以对棋盘进行任意次操作，然后交给艾莉芬再进行任意次操作，之后棋盘会进行左、下两次操作把所有积木收拢到左下角。

这是我没有做足够的验证和数学证明中的失误造成的错误，再次向各位参赛选手深表歉意。

彩色括号

• 题意、题面、题解：liu_cheng_ao
• 标程、数据：WeLikeStudying

思路

问题研究对象是满足条件的括号序列：整体合法且删掉每种单个颜色之后都合法，那么考虑怎么判断一个括号序列是否满足条件。

括号序列合法当且仅当：

1. 左右括号个数相等
2. 所有前缀和非负（将 () 分别视为 $+1,-1$）

分别考虑：

1. 由于整体左右括号个数相等且删掉红色之后左右括号个数还是相等，作差可以得到红色左右括号个数相等。同理每个颜色都如此。
2. 考虑某个位置 $i$ 的前缀和，设红绿蓝的前缀和分别是 $a,b,c$，那么 $a+b,a+c,b+c,a+b+c\ge 0$。可以发现当 $a+b,a+c,b+c\ge 0$ 同时成立时，全部相加可得 $2(a+b+c)\ge 0$。所以 $a+b+c\ge 0$ 这个条件不用单独考虑。

所以总的条件是：

1. 每种颜色左右括号个数都相等。
2. 删掉每种颜色得到的前缀和分别非负。

这是判断条件。现在我们再考虑如何用最少的修改次数让一个括号序列合法，发现：

• ) 改 ( 一定是前若干个 )，( 改 ) 一定是最后若干个 (。可以调整证明。
• 所以可以贪心：如果某种括号多，那么先改那种括号到数量平衡。然后从外往里每次将第一个 ) 和最后一个 ( 一起修改，直到前缀和全部非负为止。这就是最小修改次数。

加上颜色限制后，每种颜色内部还是符合这个条件。所以我们不妨先把每种颜色都改到数量平衡，设这样改完后的整个序列是 $a^{\prime }$。

然后设 $x_1,x_2,x_3$ 分别表示三种颜色从外往里多改了多少对括号。我们目标是最小化 $\sum x_i$。

考虑合法性对 $x_i$ 的约束，现在的约束只剩下删掉每种单个颜色时每个前缀和都必须 $\ge 0$。

对于前缀 $j$ 来说，颜色 $i$ 增加的前缀和是 $min(x_i,A_{i,j},B_{i,j})$，其中 $A_{i,j}$ 是前缀 $a^{\prime }[1,j]$ 中 ) 个数，而 $B_{i,j}$ 是后缀 $a^{\prime }[j+1,n]$ 中 ( 个数。另外设 $C_{i,j}$ 表示一开始颜色 $i$ 在 $a^{\prime }$ 的前缀和。

可以列出不等式组：

$$(\mathrm{\forall }k,j)\sum _{i\ne k}(C_{i,j}+min(x_i,A_{i,j},B_{i,j}))\ge 0$$

将 $min(\cdot ,\cdot )\ge 0$ 拆开成 $\cdot \ge 0\wedge \cdot \ge 0$ 的形式，全部整理完以及合并同类项后可以得到一个不等式组：

$$(\mathrm{\forall }S⊊U,S\ne \mathrm{\varnothing })\sum _{i\in S}{x}_i\ge C_S$$

其中 $U$ 表示所有颜色的集合 $\{1,2,3\}$，$C_S$ 是一个算出来的由 $S$ 决定的常数。

所以整个问题就是在这个约束下最小化 $\sum x_i$。因为颜色很少，三维空间上每个限制是一个平面，直接在每个面上都双指针枚举判定其它限制下的最优解即可。当颜色数更大时可以当成较一般的整数规划问题。

三种颜色的约束是在这个图的形状上求离原点曼哈顿距离最近的点：

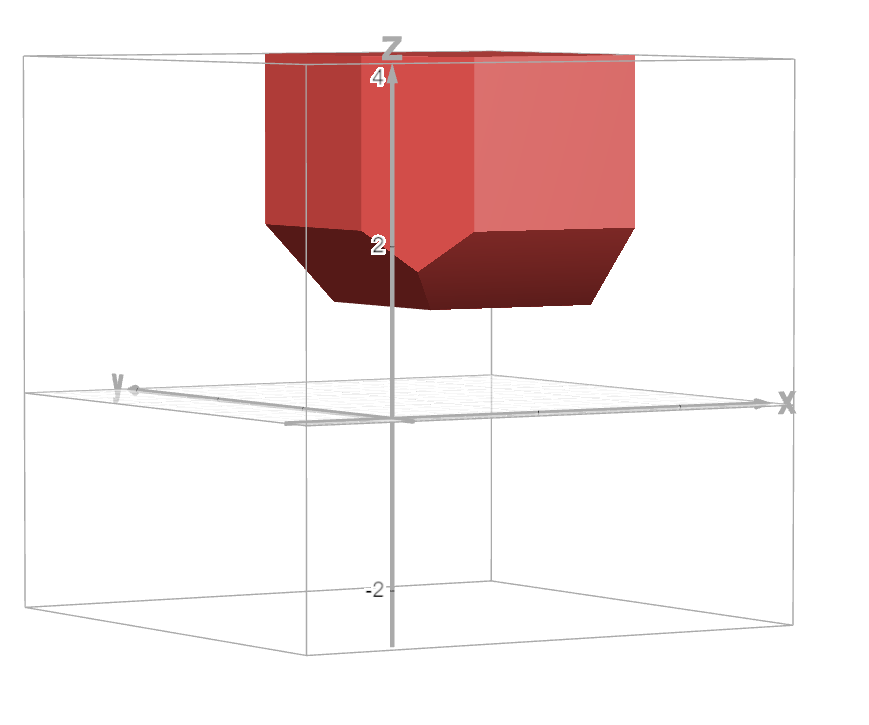
算法

按照思路所说，先做让每种颜色左右括号数量平衡必要的修改得到 $a^{\prime }$，然后枚举前缀算出 $A,B,C$ 数组，合并算出不等式组。

三种颜色的情况下，可以看成三个形如 $x_1\ge \cdot \wedge x_2\ge \cdot \wedge x_1+x_2\ge \cdot$ 的三段折线的二维偏序约束进行合并。两两枚举用双指针算出它们相交的折线，然后第三个约束在折线上的效果是约束折线只能取前一半。枚举所有折线上的点更新答案即可，一共 $O(n)$ 个。

或者你可以直接把它当成实数线性规划手算答案公式然后向上取整，在本题三种颜色的特殊情况下这是对的。

时间复杂度：$O(n)$

扩展

根据思路，显然我们可以做更多颜色的情况。设颜色数为 $k$，复杂度则为 $O(nk+ILP(k,2^k-2))$，其中 $ILP$ 是整数规划复杂度。枚举约束子集的朴素暴力算法复杂度不超过 $O(nk+2^{(2^k)})$。

本题考虑出四种颜色的情况，但鉴于选手的体验并没有这么做。

部分分

如果你没有发现不等式组，可以用双指针和区间数据结构算出每两种颜色的约束。（没有不等式组不容易发现约束只有三段，但至少可以发现是二维偏序上的阶梯型）

然后仍然可以 $O(n)$ 合并三个二维偏序约束算出答案。

时间复杂度：$O(n\log n)$

如果你只发现了一部分性质，可以做更前面的部分分。

积木对战

• 题意、题面、题解、锅：liu_cheng_ao
• 标程、数据：Yanami

思路

问题给了一个上下左右的操作方式，我们要研究它。不妨用 $LRUD$ 的序列表示操作过程。

观察问题并手玩一些例子，发现：

• 显然相邻的 $L,R$ 会抵消，相邻的 $U,D$ 也会抵消。抵消之后操作序列中 $LR$ 和 $UD$ 只能交替出现。奇数位置和偶数位置是两个子序列，分别只有 $LR$ 和 $UD$。
• 另外，形如 $RDR$ 或者 $RUR$ 这种片段，第二个 $R$ 没有效果（一个 $R$ 之后只要没有 $L$ 所有积木都是靠最右的），可以消掉。同理，$L,U,D$ 都如此。
• 所以可以推出消到最简的操作序列按下标 $(\mathrm{mod}4)$ 恰好分别是 $L,R,U,D$ 四种操作。实际上，长的操作序列只能是不断重复“顺时针转圈” $LURD$ 或者“逆时针转圈” $LDRU$。

那么一个操作序列的基本效果是 $LURD$ 的不断重复。可以发现，在操作两步之后，所有积木都到了角落，之后如果只考虑积木的存在而不考虑颜色，那么所有有积木的位置是确定的（以下用“形状”来称呼所有积木的位置集合）。我们记每行积木个数的数组为 $\{r_i\}$，每列积木个数的数组为 $\{c_j\}$，那么 $LRUD$ 依次是给这两个数组中的一个升序/降序排序而另一个不变。而一旦积木堆积到了角落里，之后无论怎么操作积木都只能堆积在角上了，这种情况下知道了 $\{r_i\},\{c_j\}$ 就能唯一确定形状。

加上颜色之后，转一圈总的效果就是在积木之间进行一个置换，对于固定的角上堆积的形状来说，置换是确定的，设为 $P$，可以算出。顺时针（$URDL$）和逆时针（$RULD$）对应的置换恰好互为逆。

（到这里我们可以解决 [ROI 2024] 2026 (Day 1) 这一问题。）

我们会发现，只要积木已经堆到了角落，那么后续它怎么操作都能逆回去。所以堆积在左下角的方案数是置换 $P$ 作用于最终状态所能得到的所有不相等的状态种类数，也就是 $|⟨P⟩(A)|$，其中 $A$ 表示最终的棋盘状态。这可以算出置换然后每个置换环上颜色列的最小正周期（复制一倍然后KMP求最大border）算出环的周期再求最小公倍数（筛法求出每个质因子次数）来得到。

然后我们要考虑不到一个周期的情况。要保证无论蔡德仁如何操作艾莉芬都能操作，所以一个必要条件是初始局面 $LD$ 和 $DL$ 两种操作得到的形状必须相同。

可以得到以下条件：

引理 1 一个矩阵 $LD$ 和 $DL$ 形状相同，当且仅当存在一行或一列为全空或全满，且删去这行/列之后的子矩阵的 $LD$ 和 $DL$ 形状相同。

• 充分性：通过操作的定义证明原来的结果等于删去这行/列后子矩阵的操作结果加上这行/列的结果，然后归纳。
• 必要性：假如不存在，那么每行每列都既有空也有积木，则 $LD$ 后第一列必定全满，$DL$ 后第一行必定全空，左上角这一格矛盾，必然形状不同。

然而，在此基础上，满足这个条件的局面在 $LD/DL$ 操作后得到的颜色分布有可能不同，且不能通过 $P$ 置换互换。所以不能直接用形状的方案数和颜色置换的方案数相乘！

反例：

010     100     100
234 [LD]200 [DL]300
050     534     254

计算出 $P$ 可以发现第二行第一个和第三行第二个位置是不会变的，所以不能通过 $P$ 互换两者，这说明该矩阵不是后面两个矩阵的合法解！

一开始的做法给这一点做了伪证，并且没有做足够的暴力验证。

做法认为：

一个初始局面是符合题目要求的，当且仅当：

• 它可以通过不断删去当前全空或全满的行/列删到空。（形状条件）
• 它在 $LD$ 之后得到的颜色分布可以被最终状态的置换生成。（颜色条件）

所以认为原问题答案等于形状的方案数乘以颜色的方案数。具体来说，形状的方案数等于 $\{r_i\},\{c_j\}$ 数组重新排序能得到的不同数组的数量，颜色的方案数如前文所述。

因此，实际上题目应该这样安排游戏规则：艾莉芬先操作一次，再让蔡德仁染色。但这样仍然需要给答案增加一些分类讨论和常数系数，因此被迫修改成现在的题面。对于现在的题意来说，这个做法是对的。

然而，原问题的困难性也没有得到证明，并且可以发现在 $LD/DL$ 之后的颜色分布可通过 $P$ 置换的情况是有一定规律的，原问题未必就没有做法。

算法

（对于没改之前的题面是假的）

形状的方案数：先算出 $\{r_i\},\{c_j\}$ 数组，然后根据数组里每种数的数量组合数计算。

颜色的方案数：算出最终状态上 $URDL$ 作用的置换 $P$ 然后求每个置换环上颜色列的最小正周期（复制一倍然后KMP求最大border），算出环的周期，再求最小公倍数（筛法求出每个质因子次数）。

两者相乘即为答案。

时间复杂度：$O(n^2)$

程序校验

题意、题面：OldDriverTree, liu_cheng_ao

题解、标程、数据：OldDriverTree

算法 1

每次暴力模拟，总时间复杂度 $O(nm)$，空间复杂度 $O(n)$。

期望得分 5 分。

算法 1.5

考虑对暴力算法进行极限卡常，但是本题操作本质串行，无法使用指令集优化。

这里介绍一种对指令集的通用攻击手段：计算连续访问数组的 L1 缓存缺失量。

强制在线会导致遍历数组时发生大量的 L1 缓存缺失。

为了卡常到极限，利用取模生效次数很少的性质，可以将 $a$ 数组和 $l$ 数组预处理的时候进行合并，这样对于每个位置，只会进行 3​ 次 ​8​ 字节的数组访存。

评测机的 CPU 的 L1 缓存行大小为 32B 的数据缓存和 32B 的指令缓存，每个核心的 L1 缓存总大小为 32KB 的数据缓存和 32KB 的指令缓存。L1 缓存命中时需要约 $4\sim 5$ 时钟周期，缺失时需要约 $12\sim 14$ 时钟周期。（这段是问 deepseek 的，该数据大致复合正常 CPU 的表现）

如果暴力算法可以通过，则 1s 处理遍历数组时发生的 L1 缓存缺失次数为 ${10}^5\times 5\times {10}^5\times 3\times 8/32/10=3.75\times {10}^9$，由于 CPU 的频率是固定的，所以对时钟周期进行计算可以发现该数据远远超过 CPU 访存极限。

不过对于数据范围较小的测试点，有优化后的暴力算法获得了非平凡的分数。

期望得分 5~15 分。

算法 2

针对 $d_i=0$ 的情况，观察发现取模最多进行 $O(\log v)$ 次，因为每次取模都会导致 $v$ 减半。

考虑每次使用数据结构高效找到接下来第一次该数会发生取模的位置，等价于给定 $x,v$，求 $x$ 后面最近的一个区间，使得区间包含了 $v$。

这个问题可以倒着从后往前维护持久化值域线段树，维护每个值最近被覆盖的时刻，每次加入一个区间的时候做区间染色。

于是对每个位置 $i$，我们有一个持久化值域线段树，支持给定 $v$，查询从 $i$ 开始 $v$ 第一次被覆盖到的时刻。

总时间复杂度 $O(n\log v+m{\log }^{2}v)$，空间复杂度 $O(n\log v)$。

期望得分 15 分。

算法 3

如果所有询问的 $R$ 都等于 $n$，有一种持久化平衡树做法。

先考虑简化的，没有 $l_i,r_i$ 限制，并且 $d_i=0$ 的问题。

倒着维护每个后缀的函数复合结果，$f[i][j]$ 表示从 $i$ 开始，初始是 $j$，经过函数复合后到 $n$ 位置的值是多少。

初始是 $f[n][i]=i$ 的恒等映射，使用所谓的 “整体DP” 的思路，还是从后往前倒着维护，每次在原函数复合结果 $f[i+1]$ 前加一个新的函数复合得到 $f[i]$ 时做一个区间复制。注意到这里需要将一个区间变成另一个区间复制多次，这个可以用倍增合并的方法实现单次 $O(\log v)$。

特别需要注意的是，对于持久化 treap 来说，区间复制 $k$ 次的倍增合并是 $O({\log }^{2}v)$ 的，而对于其他拥有更加优秀性质的平衡树（如 WBLT，AVLT），该操作是 $O(\log v)$ 的。

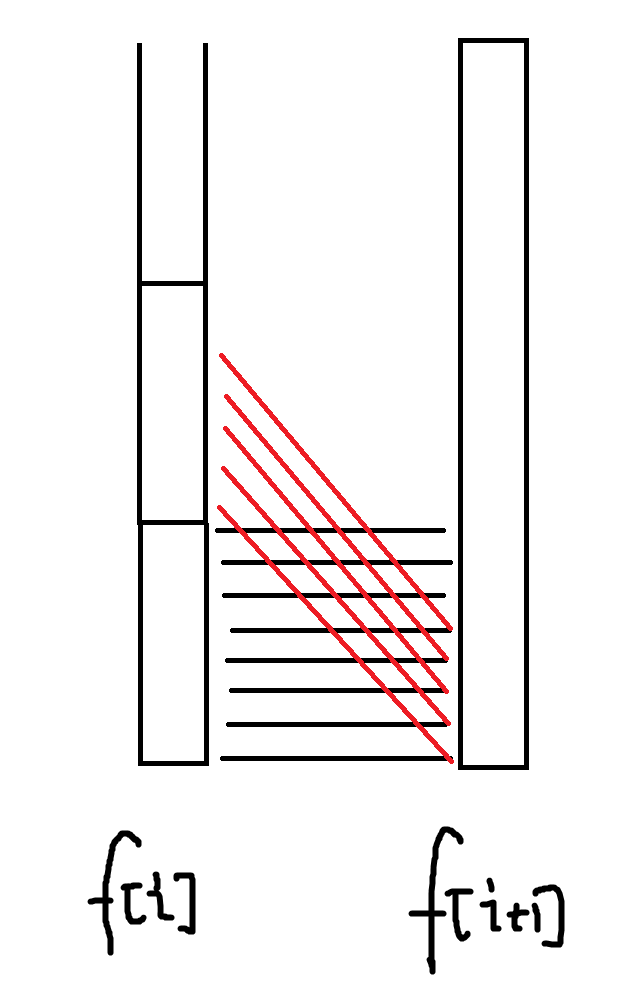
这样可以 $O(n\log v)$ 预处理出每个后缀的持久化平衡树，支持每次 $O(\log v)$ 查询给定 $x$ 和 $l$，求 $x$ 经过 $[l,n]$ 区间函数复合后的结果。

再考虑如果有 $l_i,r_i$ 的限制，并且 $d_i\ne 0$ 该怎么办。可以发现持久化平衡树功能非常强大，区间的限制可以通过每次对 $f[i]$ 只修改其 $[l_i,r_i]$ 部分，其他部分保持不变来实现。$d_i\ne 0$ 可以通过每次对 DP 数组做一个区间平移操作实现，可以用持久化平衡树的操作简单实现。

针对 $R=n$ 的情况，总时间复杂度 $O(n\log v+m\log v)$，空间复杂度 $O(n\log v)$。

期望得分 35 分。

算法 4

回顾算法 2，持久化值域线段树功能受限无法进行区间平移和复制操作，考虑将其换成持久化平衡树来支持更强的操作。

于是倒着从后往前维护持久化平衡树，维护每个点最近被覆盖的时刻，每次的操作有区间染色，区间复制，分裂合并等，都是持久化平衡树支持的操作。

对每次查询，使用预处理好的数据结构每次 $O(\log v)$ 找到最近一次取模的位置，需要取模 $O(\log v)$ 次。

总时间复杂度 $O(n\log v+m{\log }^{2}v)$，空间复杂度 $O(n\log v)$。

期望得分 55~75 分。

算法 5

我们发现对于 $R=n$ 我们可以每次 $O(\log v)$ 查询出答案，所以可以对序列分治建立线段树，对线段树的每一层，问题变成 $L=1,R=n$ 的子问题。

每次查询需要按顺序找到 $[L,R]$ 区间的 $O(\log n)$ 个线段树结点，将 $v$ 依次代入得到经过区间函数复合后的结果。

这个方法可以顶层分块，底层分块，将线段树变成多叉线段树来极大地减少常数。

顶层分块：可以发现线段树的根结点的没有用的，只有 $L=1,R=n$ 的查询才会用，所以可以不建立。继续分析可以发现线段树的最上面几层如果拆掉后，会减少预处理复杂度，少量增加查询复杂度。

底层分块：可以发现线段树的叶子结点是没有用的，如果建立的持久化平衡树，则每次查询是 $O(\log v)$ 的，还不如暴力。于是可以底层区间很小时直接暴力计算答案。

多叉线段树：可以发现线段树加上底层分块和顶层分块后二叉就不优了，于是将线段树改为多叉的。

利用右儿子：可以发现线段树结点可以直接从其右儿子处继承过来持久化平衡树，然后只需要将左儿子的部分插入即可。

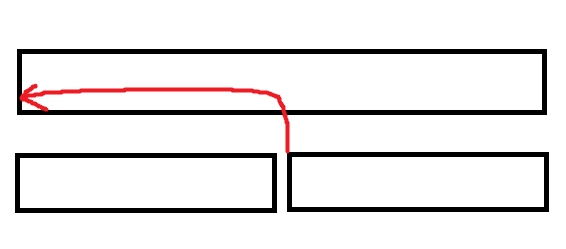
利用左侧查询的优势：可以发现询问的部分如果是某个线段树结点的后缀，则可以不用暴力，而是用持久化平衡树的一次查询代替。

总时间复杂度 $O(n\log v+m{\log }^{2}v)$，空间复杂度 $O(n{\log }^{2}v)$。

这个算法没有利用取模的特性，所以不优，在其他没有好的性质的题中是已知的最优做法。

利用以上技巧极限卡常后，期望得分推测为 55~85 分。

算法 6

我们考虑使用 “全局平衡” 的思想，类似于树链剖分套线段树的那种问题，每次查询如果需要在 $O(\log n)$ 个子问题上花费 $O(\log n)$ 的代价二分，导致复杂度是 $O(\log n)\times O(\log n)=O({\log }^{2}n)$，如果将两种二分的结构套起来，构造出一种常数层减半的结构，就可以做到 $O(\log n)+O(\log n)=O(\log n)$。

我们在这个问题上，尝试将一开始的持久化平衡树的做法进行拓展，使得其可以进行区间查询，并且将第二，四种暴力做法的思想结合进去，即利用每次只会发生 $O(\log v)$ 次取模的特性。

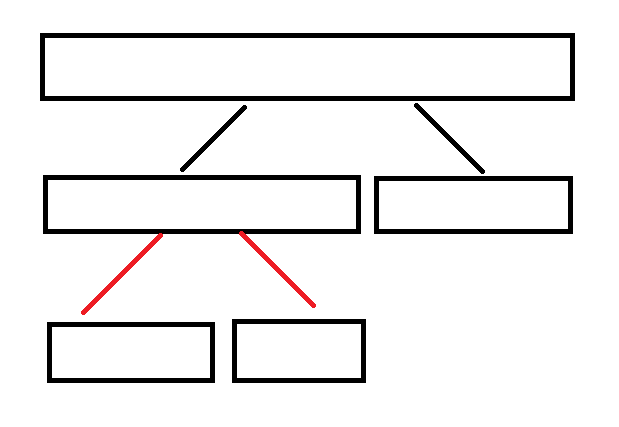
我们在持久化平衡树上维护每条边的边权，有两种颜色的边，分别是红色和黑色。红色的边的含义是下方结点是某次取模导致的区间复制复制产生的，黑色的边的含义是正常持久化平衡树的边。

每个叶子结点到根结点的路径上最多只有 $O(\log v)$ 条红色的边，因为每走一次红色的边相当于找到了一次发生取模的事件，取模的性质保证只能发生 $O(\log v)$ 次取模。同时由于持久化平衡树是平衡树，所以可以保证每个叶子结点到根结点的路径上最多有 $O(\log v)$ 条黑色的边。

具体实现的时候，我们需要对每条红色的边记录下这条边是序列上哪个位置产生的，持久化平衡树的重新平衡（如旋转）仅限于对黑色的边，对红色的边是不做重新平衡的。平衡操作可以看做是产生新的边，以及将原本两条新的边压缩为一条边。由于我们是通过红色的边来找到每次取模的位置的，所以重新平衡的时候对红色的边做平衡操作会使得找取模位置的时候少找了一些，只能对黑色的边做操作。

每次查询 $[l,r]$ 区间，输入 $v$ 时，先在 $l$ 位置的持久化平衡树根结点上开始查询 $v$，在查询的过程中每次走一条红色的边则意味着发生了一次取模，走黑色的边则是为了保证持久化平衡树的深度所必须走的。这样我们可以用 $O(\log v)+O(\log v)=O(\log v)$ 的时间复杂度找到 $[l,r]$ 区间查询时所发生的所有取模事件。在递归查询的过程中如果发现走到了一条时间 $>r$ 的红色的边，则不需要继续递归了。

其实可以进一步解释本题做法，我们需要维护一个 DAG 结构，使得从任何点出发，该 DAG 深度是 $O(\log v)$ 的。虽然暴力的计算图的 DAG 深度是 $O(n)$ 的，但是我们只关心取模的位置，所以对于不是取模的操作可以将其合并在一起来减少 DAG 的深度。利用持久化平衡树深度以及取模次数的性质，可以构造出一个满足我们要求的 DAG 结构，每次查询本质上是在预处理好的深度 $O(\log v)$ 的 DAG 结构上进行 DFS。

本做法对于其他持久化平衡树做法有显著优势，因为其他做法需要多次查询持久化平衡树，本做法只需要一次查询，虽然本做法的平衡树由于“全局平衡”的性质所以常数比正常平衡树大。

总时间复杂度 $O((n+m)\log v)$，空间复杂度 $O(n\log v)$。

期望得分 100 分。