逛公园

from Lagoon

算法一

每个点都跑一遍最短路，复杂度 $O(nm\log n+\sum k^2)$ 。

期望得分 5 分。

算法二

树上的时候是一个经典的点分治 / 虚树 DP，复杂度 $O((n+\sum k)\log n)$。

期望得分 25 分，结合算法一能获得30分。

算法三

仙人掌上的时候还是一个经典的点分治 / 虚仙人掌 DP，复杂度 $O((n+\sum k)\log n)$。与本题的主题关系不大，就不详细讲了。

期望得分 45 分，结合算法一能获得 50 分。

算法四

仙人掌上加一条边的话可以考虑将点分治算法做一些修改。

将这条边单独提出来，求出其端点到所有其它点的最短路，然后删去。

这样点分治时两点最短距离就变成了仙人掌上最短距离和经过该边的最短距离取 $min$，然后稍微判一下就好了。

复杂度 $O((n+\sum k)\log n)$。

期望得分 55 分，结合算法一能获得 60 分。

广义串并联图

题目给定的图的条件等价于这张图不存在同胚于 $K_4$ 的子图，这种图被称为广义串并联图。

广义串并联图的一个基本处理方法就是进行收缩操作并建立串并联树，具体如下：

若图中存在点度为 $1$ 的点，直接将其删除，称其为删 $1$ 度点操作。

若图中存在一对重边，将其合并成为一条，合并成的新边的长度为这一对重边长度的较小值，称其为叠合重边操作。

若图中存在点度为 $2$ 的点，如果与该点相连的两条边是一对重边，则先进行叠合重边操作；否则设与该点相连的两个点分别为 $x,y$ ，删除这个点和与其相连的边，在 $x,y$ 之间建立新边，新边的长度为被删除的两条边的长度之和，称其为缩 $2$ 度点操作。

可以证明，任意广义串并联图都可以在若干次缩 $2$ 度点、叠合重边、删 $1$ 度点的操作后变为一个只包含一个节点的图。

证明相当复杂，具体可以看吴作同 IOI 2019 中国国家候选队论文《〈公园〉命题报告》 （前传） 。

然后建立串并联树：

1、对于删 $1$ 度点操作：建立一个新的节点 $v^{\prime }$，将被删除点 $x$，与其相连的边 $a$ 和 $a$ 的另一个端点 $z$ 对应的树上节点 $v_x,v_a,v_z$ 的父亲设为 $v^{\prime }$，然后将点 $z$ 对应的树上节点设为 $v^{\prime }$。

2、对于叠合重边操作：建立一个新的节点 $v^{\prime }$，将两条重边 $a,b$ 对应的树上节点 $v_a,v_b$ 的父亲设为 $v^{\prime }$，然后将合并后的边对应的树上节点设为 $v^{\prime }$。

3、对于缩 $2$ 度点操作：建立一个新的节点 $v^{\prime }$，将被删除点 $x$ 和与其相连的两条边 $a,b$ 对应的树上节点 $v_x,v_a,v_b$ 的父亲设为 $v^{\prime }$，然后将建立的新边对应的树上节点设为 $v^{\prime }$。

这个串并联树中，每一个树上节点唯一对应图上的一个点或一条边，初始图 $G$ 中每一个点或一条边唯一对应一个树上叶子节点，且每一个非叶子节点也对应一个收缩操作。

事实上，这个串并联树和 top cluster 是差不多的，但由于我不太会 top cluster，所以我也不懂具体啥样。

算法五

对于子任务 7，相当于多次求广义串并联图上两点 $a_1,a_2$ 之间的最短路径长度。

我们发现串并联树上的一个点 $u$ 的子树在原图上也对应着一个类似于子树的结构：

定义串并联树上节点 $u$ 的内部图 $G_u^{\prime }$ 为初始图 $G$ 的一个子图。

1、如果点 $u$ 在图上对应的是一个点，那么对于初始图 $G$，如果图上的一个点或一条边对应的树上叶子节点在点 $u$ 的子树中，那么这个点或边属于 $G_u^{\prime }$。

2、如果点 $u$ 在图上对应的是一条边，设这条边为 $(x,y)$，那么对于初始图 $G$，如果图上的一个点或一条边对应的树上叶子节点在点 $u$ 的子树中，那么这个点或边属于 $G_u^{\prime }$，且点 $x$ 和点 $y$ 也属于 $G_u^{\prime }$。

于是我们可以在串并联树上设计一个“内部图” DP：

如果点 $u$ 对应的是一个点，那么我们设它对应的那个点为其内部图的一个端点 $b_1$ ，否则它对应一条边，我们设它对应的那条边的两个端点为其内部图的两个端点 $b_1,b_2$。

设 $f_{u,i,j}$ 为只保留 $u$ 的内部图时询问点 $a_i$ 到端点 $b_j$ 的最短路径长度； $h_u$ 为只保留 $u$ 的内部图时询问点 $a_i,a_2$ 的最短路径长度（如果有询问点不在内部图 $G_u^{\prime }$ 中 $h_u=+\mathrm{\infty }$）；如果内部图 $G_u^{\prime }$ 有两个端点，就再设 $g_u$ 为为只保留 $u$ 的内部图时这两个端点间的最短路径长度。

这样做一次 DP 就能求出一次询问的答案，即 $h_{root}$ 。多组询问可以用 DDP，将转移写成矩阵形式，然后倍增求出链上矩阵乘积即可。

复杂度 $O((n+q)\log n)$。

期望得分 25 分，结合算法一、四能获得 85 分。

算法六

对于一般情况，我们希望把树分治算法再改造一下。

由于串并联树是一个三叉树，可以直接进行边分治，且边分治仅会将树分成两个部分，比起会将树分成多个部分的点分治来说需要考虑的情况要简单得多，因此这里采用边分治而非点分治。

边分治时每次找到一条边并将树按照这条边分开。

考虑这条边的两个端点，它们一定是儿子-父亲关系，设其中的儿子为点 $u$ ，那么就变成了每次考虑 $u$ 的子树内到 $u$ 的子树外的答案。

再定义外部图为：

一个串并联树上节点 $u$ 的外部图为先进行所有在点 $u$ 子树内的收缩操作后的图。

那么对于串并联树上节点 $u$，它内部图和外部图的点集的并为整张图的点集，且：

如果 $u$ 对应一个点 $x$，那么其内部图和外部图点集的交恰为 $\{x\}$；否则如果它对应一条边 $(x,y)$，那么其内部图和外部图点集的交恰为 $\{x,y\}$。

我们称点 $u$ 内部图和外部图点集的交为它的分割点，它有一到两个分割点，记为 $p_1,p_2$（$p_2$ 可能不存在）。

然后统计所有询问中所有满足 $x$ 属于内部图且 $y$ 属于外部图的点对 $(x,y)$ 的贡献。

由上述结论，它们之间的路径至少会经过 $p_1,p_2$ 其中之一，分类讨论，得出其最短路径长度为：

$$dis(x,y)=min\{dis(x,p_1)+dis(y,p_1),dis(x,p_2)+dis(y,p_2)\}$$

这个 $min$ 取到哪一边和 $(dis(x,p_1)-dis(x,p_2))+(dis(y,p_1)-dis(y,p_2))$ 的正负性有关，因此可以将所以图中的点 $x$ 分别按照 $dis(x,p_1)+dis(x,p_2)$ 排序，然后直接双指针扫描即可统计答案。

统计完答案我们就可以将外部图和内部图直接拆开，然后如果 $p_2$ 存在，那么我们需要在外部图和内部图的点 $p_1,p_2$ 之间都加上一条长度为 $dis(p_1,p_2)$ 的边（这里的 $dis$ 为整张原图上的最短路径长度），这样就能保证外部图和内部图内部的点对之间最短路径长度不变。

该算法时间复杂度为 $O((n+K){\log }^{2}n)$。

期望得分 100 分。

快递公司

from shiliangzhi

道歉

出题人在出题时并没有注意到有论文研究过 $50$ 个点 $4$ 种颜色的构造，因此本题造成了一些事故，出题人给大家道歉，求轻喷。

测试点一

$n=5$ 应该非常好想，显然两个五元环可以直接拼出完全图。

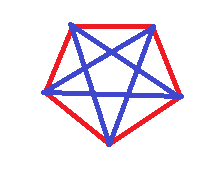
测试点二

$n=8$ 时，不难证明其至少需要 $3$ 种颜色（具体证明见下文）。

观察到 $8=2^3$ ，不难想到分治。先把 $8$ 分成 $4+4$ ，这两组之间的点相互连颜色 $1$ ，然后各组分成 $2+2$ ，相互之间连颜色 $2$ ，剩下的边就是颜色 $3$ 。

测试点三

我们观察到 $16=2^4$，那么就按照测试点二的方法，使用 $4$ 种颜色构造？

因为该测试点是 $10$ 分，所以很显然不会那么简单，因此肯定需要用 $3$ 种颜色构造。

测试点三--算法一

我什么都不会，只知道有三种颜色怎么办？每条边只有三种颜色，直接爆搜，这样也许在有生之年可以出解。

测试点三--算法二

注意到 $16$ 已经很难构造了，所以猜想 $16$ 是三种颜色的上界。

如果真的是上界，那么方案一定有非常强的对称性，因此每一个点所连出去的 $15$ 条边一定平分三种颜色。也就是说，每个点连出去的边每种颜色恰好占 $5$ 条。这样就可以剪枝啦！

估算一下搜索时间：当 $n=10$ 时实测 $0.05\mathtt{\text{s}}$ ，当 $n=13$ 时实测 $111.1\mathtt{\text{s}}$。众所周知，搜索的时间是指数型增长的，因此当 $n=16$ 时应该要搜……

似乎一个晚自习是不能出解的。

测试点三--上界证明

爆搜好像有点困难，那么就要想别的方法。

记 $f_i$ 表示 $i$ 种颜色能表示的上界，不难得出 $f_1=2$ 。

对于 $f_2=5$ ，这在图论中是一个经典模型：六个人中至少有三个人相互认识或相互不认识。这个问题的证明方法是随便选择一个点，然后让它的连出去的边颜色平均，在 $n=5$ 时每个点会连出去 $4$ 条边，每种颜色占 $2$ 条。其中，同种颜色的 $2$ 个点之间显然不可能连这种颜色，所以相当于这两个点中少了一种颜色可以连。

因此 $f_2\le 2f_2+1=5$ 。

同理，我们可以得出 $f_3\le 3f_2+1=16$ 。

测试点三--算法三

有了证明后就好想多了，只需要先选择一个点，然后连出去 $15$ 条边，每 $5$ 个点分一组，这一组中是一个 $n=5$ 的问题。

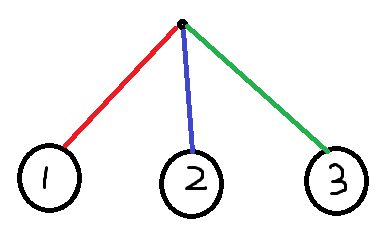
即选择的这个点未为 "领队" ，其他 $15$ 个点为 "组员"，每一组的颜色定义为 "领队" 向 "组员" 连的边的颜色。

现在只需要解决三组点之间相互连边的问题。（现在爆搜就快多了）

通过计算，任意两组之间需要连 $5$ 条不属于各组颜色的边，另外两种边各占 $10$ 条。例如：$1$ 和 $2$ 两组之间需要连 $5$ 条绿边，$10$ 条红边和蓝边。

此时猜想绿边是点与点对应连边，红边和蓝边再按照不冲突的方式排一下，其他组之间的边就是颜色的循环位移。这样就构造出来了。

测试点四、五

在测试点三中证明了 $f_3=16$ ，所以 $25$ 开始只能用 $4$ 种颜色构造。

通过观察，$25=5\times 5,32=2\times 16$ ，所以可以直接套用测试点二的做法。

测试点六、七

注：从测试点六开始往后的所有测试点也许有更优解法。

观察到 $33=32+1，34=32+2$ 所以考虑在 $2\times 16$ 的基础上在加上一或两个点。

如果把 $16$ 看成一个整体好像很难做，而在构造 $n=16$ 时有一个天然的分组，考虑利用这个分组。

对于 $n=33$ 可以把每个团中那个 "领队" 的节点之间连的 $4$ 换成 $1,2,3$ 中任意一种，在引入一个 "统领" 两个团中 $30$ 个点的节点，这个节点和这两个领队之间连 $4$ 。

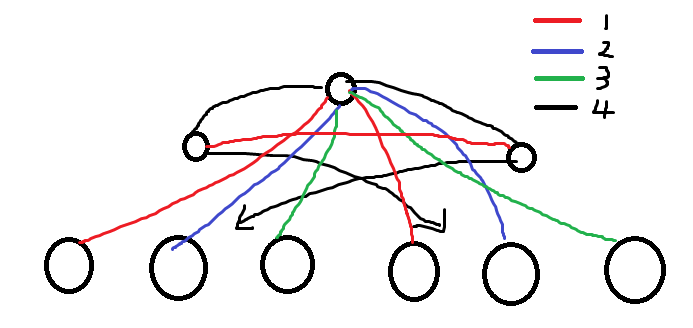
对于 $n=34$ 可以给每个团引入两个 "领队" ，两个领队之间连接颜色 $4$ 。（图中为了方便画图，每一组上方的两个点是另一组的两个领队。领队和组员之间连的边是 $1,2,3$ 中的某一种。）

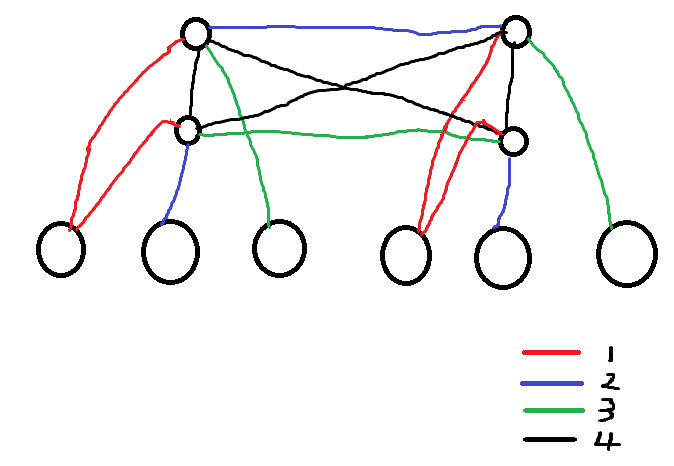
既然两个 "领队" 之间连了颜色 $4$ ，那么它们对面的 "组员" 不能在同一个点上都连 $4$ ，那么可以一个连 $1,2,4$ ，一个连 $1,4,3$ 。

对于两个 $1,2,4$ 的领队，颜色 $3$ 空出来了，所以它们之间可以连 $3$ ；同理，两个 $1,4,3$ 之间可以连 $2$ ；交叉的点就连 $4$，这样 $4$ 也只会形成四元环，不会形成三元环。

测试点八、九、十

注意：该部分的两张图仅为示意图，图中画出的边仅为示意，并未完全画出。

通过测试点三中的上界计算，可以算出 $f_4\le 65$，所以 $80,82,85$ 都是 $5$ 种颜色。

由于 $80=5\times 16$ ，所以和测试点二一样做。

由于 $82=80+2$，所以尝试多加入两个点。这部分和 $n=33$ 比较像，就是 $5$ 个"领队"之间的颜色换成另外两种，这样引入的点就可以和这 $5$ 个“领队”之间连同一种颜色。两个引入点之间在随便连一条没有冲突的颜色。

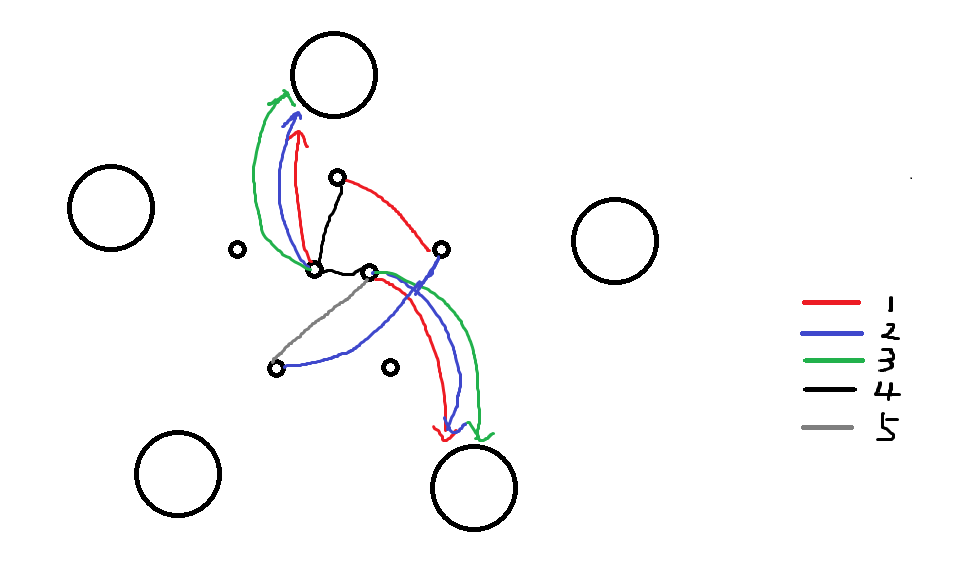
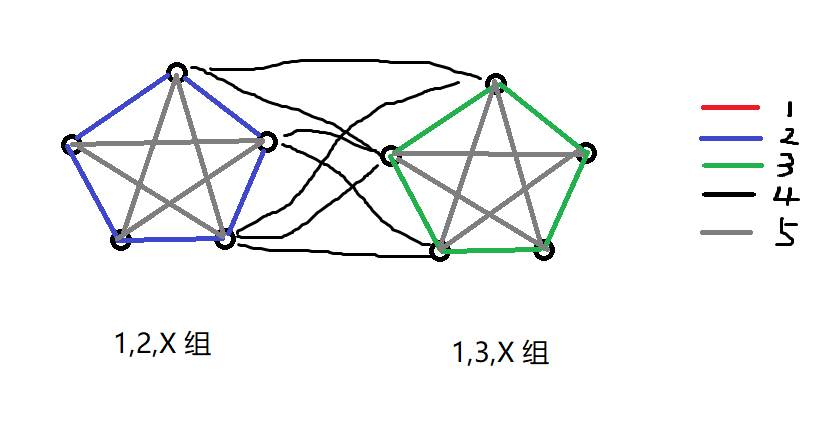
由于 $85=80+5=75+2\times 5$，因此这部分和 $34$ 比较像，即每 $15$ 点引入两个领队，领队与该组的三个团分别连 $1,2,3$。这两个点中的一个点与其他组的团连 $1,2,X$ ，另一个连 $1,3,X$。（$“X”$ 为颜色 $4$ 或 $5$ 。）

这 $10$ 个领队按照 $1,2,X$ 和 $1,3,X$ 分成两组，每组 $5$ 个点。显然 $1,2,X$ 这一组点之间可以用 $3,5$ 两种颜色相连，$1,3,X$ 这一组点之间可以用 $2,5$ 两种颜色相连，两组之间的点可以用颜色 $4$ 相连。

小 C 的比赛

from rushcheyo

猜想：如果数集中存在一对相反数 $a$ 和 $-a$（$a>0$），那么存在一种最优方案使得序列的开头为 $a$ $-a$。

悬赏：以上命题的正确性，在无值域限制时我并不确定，经过大量对拍我认为其很可能正确。如果能证明或证否此命题的同学，可与管理员联系领取 UOJ 抱枕一个。

UPD：已经被 hos_lyric 解决，命题错误，反例如下：

441 -441 106 -531 53 664 -901 -123 -254 75 404 629 -71 408

以下将会说明，这个猜想在 $[-2,2]$ 内是正确的，并能导出标算。

注意答案有一个明显的下界：$r=max(\sum x_i,max{x}_i)$。

首先我们用猜想中的规则消去所有 $0$ 和相反数，现在剩下数的值域只有这几种情况：

1. $\{1,2\}$ 或 $\{-1,-2\}$，任意排布即可取到 $r$；

2. $\{-1,2\}$，我们将尽可能多的 $\mathtt{\text{2 -1 -1}}$ 放在序列开头；之后剩下两种情况：

   1. 全是 $-1$ 或全是 $2$，则取到了 $r$；

   2. 除了一个 $-1$ 外全是 $2$，随意排布（但除非 $n=2$，否则 $-1$ 不能放在序列两端）即取到 $r$。

3. $\{-2,1\}$，用 2. 中的类似办法，但此时 $\mathtt{\text{1 1 -2}}$ 中的 $\mathtt{\text{1 1}}$ 可能对答案也有贡献，需特判一下答案是否为 $1$（此时 $1$ 和负数交替，也符合猜想）。