新年快乐！大家打得开不开心呀！

“一起AK吧”

长度测量鸡

from nneztlk

算法一

直接枚举刻度, 时间复杂度为 $O\left((\genfrac{}{}{0ex}{}{n(n+1)/2-1}{n-1})\right)$. $n=5$ 时这个数是 $(\genfrac{}{}{0ex}{}{14}{4})=1001$, $n=8$ 时这个数是 $(\genfrac{}{}{0ex}{}{35}{7})=6724520$. 期望得分 $10\sim 20$ 分.

算法二

我们需要题目描述中的 $s_j-s_i(0\le i<j\le n)$ 这 $\frac{n(n+1)}{2}$ 个数取到 $1\sim \frac{n(n+1)}{2}$ 的所有整数, 所以每个整数只能取一次, 即每种长度只能被一种方法量出. 特别地, $s_i-s_{i-1}(1\le i\le n)$ 这 $n$ 段长度两两不同, 故只能是 $1,2,\dots ,n$ 的一种排列.

枚举排列, 时间复杂度为 $O(n!)$. $n=8$ 时这个数是 $40320$. 期望得分 $20$ 分.

算法三

事实上, $n=1,2,3$ 时可以直接试出刻度方案, 分别为 $\varnothing ,\{1\},\{1,4\}$, 而对所有 $n>3$ 都不存在满足要求的刻度. 证明如下:

记 $M=\frac{n(n+1)}{2}$, 则对 $n>3$, $M\ge 10$. 现假设存在满足要求的刻度方案. 由于需要量出 $M-1$ 的长度, 所以 $1$ 或 $M-1$ 处必须有刻度, 由对称性不妨设 $1$ 处有. 要量出 $M-2$ 的长度, $2,M-2,M-1$ 中需要有一处有刻度, 而如果 $2$ 或 $M-1$ 处有刻度, 则可以用两种方法量出长度 $1$, 矛盾! 所以 $M-2$ 处必须有刻度. 此时由 $(M-2)-1=M-3$, $M-3$ 的长度已经可以被量出. 要量出 $M-4$ 的长度, $2,4,M-3,M-4$ 四处必有一处有刻度. 容易发现只有 $4$ 处的刻度不会引起重复.

现在已经知道 $1,4,M-2$ 处都需要有刻度, 而长度 $M-5$ 尚未被量出. 欲量出 $M-5$, 需要 $3,5,M-5,M-4,M-1$ 中的一处有刻度. 然而它们都会导致 $1,2,3$ 中的某个长度能被两种方法量出, 矛盾! 故不存在满足要求的刻度.

所以只需判断 $n$ 是否大于 $3$. 时间复杂度 $O(1)$, 期望得分 $100$ 分.

直径拆除鸡

from szy042

算法一

输出一朵花，就像 $(1,2),(1,3),(1,4),\dots$

讲真这样子对于 $n\le 10$都是对的

然而当 $n=11$ 时就开始挂啦

期望得分 20

算法二

输出一棵二叉树

（我没什么想说的

期望得分 $10$

结合算法一可以得30分

算法三

枚举树，按照题意模拟

找到一个最大的输出

UOJ的评测机很萌，所以能比算法一多十分~

期望得分：30

结合算法二，可以得40分

算法四 开花的金字塔

思考一下一棵树被删除一条长为x的直径之后的情况，我们发现，剩余的连通块中的直径最长为 $(\lfloor x/2\rfloor -1)\times 2$。

证明是容易的。考虑这棵树原来的直径 $a$ 和删除之后最长的直径 $b$。我们取 $a,b$ 上最近的两个点 $c,d$，$c,d$ 两点把 $a$ 和 $b$ 分别分成两部分，各选取较长部分，加上 $c,d$ 之间的链，共同组成一条链，链长度的最小值就是 $\lfloor (a+1)/2\rfloor +\lfloor (b+1)/2\rfloor +1$，这条链的长度要小于原直径a，所以b不能大于 $(\lfloor a/2\rfloor -1)\times 2$。

从取整符号可以看出，直径长度是偶数可以让 $b$ 最大，此时 $b=a-2$。

然后考虑一棵树被删除之后的连通块个数，除了最后一次删除，每多一个连通块，每个点被算入代价的次数显然会减少，于是就启发我们构造一个删除过程中不出现新的连通块的图，与上面的删除直径相联系，我们就可以随手构造一个符合条件的图出来。

将节点数分别为 $1,3,5,7,\dots$ 的链的中点相连，这就是一个符合要求的图。什么？你问多出来的那些点怎么办？扔到长度为 $3$ 的链的中点上（前面的字数太多于是后文称之为天上），变成一座开花的金字塔。考虑这些多出来的点对代价的贡献，放到天上的正确性是显然的。

期望得分：50

结合算法一/三可以得到60

算法五

我们发现算法四还需要结合算法一/三才能获得 60 分，因为算法四没有办法通过 $n=9$ 的测试点，于是，我们发现链的条数不是越多越好。因为一方面，链数增多可以让天上的结点的递归层数增加，但另一方面链数增多需要囤积更多的递归层数很浅的结点。所以我们需要枚举链的条数，将多出来的扔到天上，如果结果大于 $m$，输出之。

期望得分 100。

啊严谨证明是：用 $f[n][p]$ 表示有 $n$ 个节点直径长度为 $p$ 的最多删除次数，用前面得到的删除一条直径后的直径长度关于 $p$ 的不等式搞一搞，就能列个递推式。可以用数学归纳法证明 $f[n][p]=kn-b$，其中 $k$ 和 $b$ 是某个关于 $p$ 的常数。观察 DP 的取值，就能反向构造出对应的最优解了，发现恰好就是上面那样是最优的。

快乐游戏鸡

from scPointer

算法一

注意到当当前死亡次数不变的时候，整棵树上可走的点和边也是不变的。 考虑把每个点拆成 $max\{w_i\}$个点，然后跑分层图就好了。

或者你可以设一个状态 $f[i][j]$ 表示死亡 $i$ 次，当前在结点 $j$ 的最短时间然后跑dp。

后者的复杂度是 $O(nqmax\{w_i\})$ 的。这样可以通过子任务 $1$ 拿到 $10$ 分。

算法二

你可以发现每次从点 $s$ 出生到撞程序猿死亡跟前几次是怎么死的并没有关系。所以对于每次 “从点 $s$ 出生到撞程序猿死亡” 的过程都可以贪心选最近的点早死早超生。如果暴力BFS贪心的话复杂度是会炸的，离散化权值也不行。

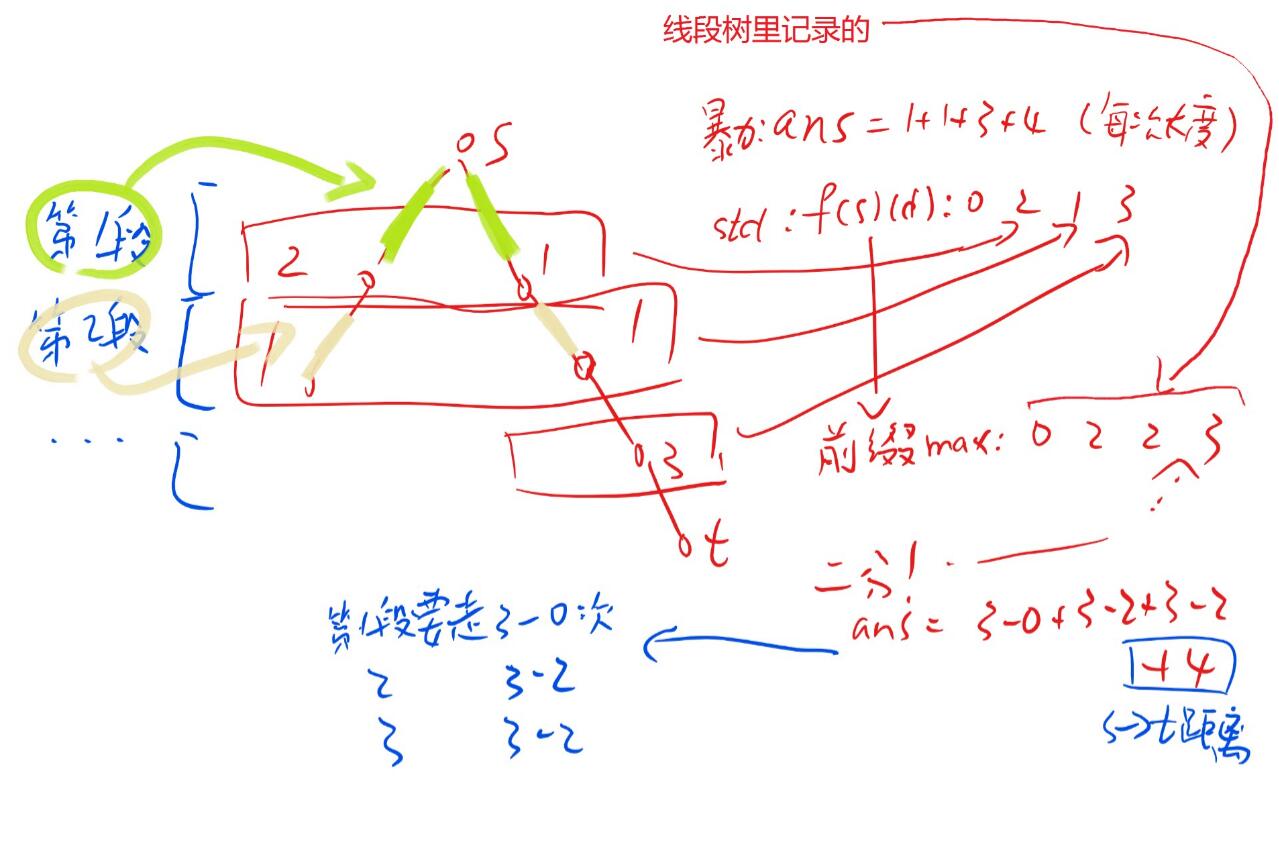
我们换个角度，考虑有多少次从出生到死亡的过程需要一秒，多少次需要两秒等等。

具体来说，考虑记录 $f[i][j]$ 表示 $i$ 的子树中和 $i$ 距离小于等于 $j$ 的点的权值最大值。 这样 $f[i][j]-f[i][j-1]$ 就等于有多少次从出生到死亡需要 $j$ 秒。 那么只要从 $0$ 开始枚举 $j$ 把贡献加起来，直到 $s$ 和 $t$ 联通的时候直接从 $s$ 走到 $t$ 就好了。

复杂度 $O(n^2+nq)$ ，可以通过子任务 $1,2$ 拿到 $20$ 分。

算法三

算法3-1

因为所有 $s=1$ 所以就可以把算法 $2$ 里 $f$ 的第一维删掉辣。然后把 $f$ 搞搞差分前缀和什么的，每次询问二分就好了。复杂度 $O(n+qlogn)$ 。

算法3-2

或者...让我们回到算法二的第一段。如果你只想到贪心没有想到记录 $f$ 数组，那么第三个部分分也是可以拿的。首先对询问的每个终点按照能到达那个终点的死亡次数排序，然后算法二第一段的贪心过程可以用一个堆或者set来做。

如果一个点可以被到达（可以安全通过它的父亲了），就扔进来，如果死亡次数大于等于某个点的权值（可以安全通过它自己了），就扔出去。当前死亡次数达到某个点的死亡次数的时候就处理一下询问就好了。复杂度 $O(q+nlogn)$ 。

这两个算法和场上可能出现的各种我可能没想过的算法可以通过子任务 $3$ ，这样就有 $40$ 分了。

算法四

算法4-1

为了方便叙述，我们把点 $1$ 放在最左边，点 $n$ 放在最右边，拉成一条链。

然后把所有询问按照左端点从右向左排序，处理 $f$ 数组的时候也从右向左处理。然后观察一下每次往左扩展一个点的时候 $f$ 数组有啥变化，然后你机制的发现这个是可以用线段树转移的，询问也可以在线段树上查询。

等一下！每次加一个点的时候好像是区间对一个数取max唉，是不是要强上一波segment tree beats(吉司机线段树)啊。如果是场上真的有选手卡在这里的话，我表示非(xiao)常(chu)遗(sheng)憾。回到算法 $2$ 看一眼 $f$ 的定义你会发现这玩意是单调递增的，所以我们二分出线段树上最后一个小于要更新的那个数的地方，然后区间覆盖就可以了。

稍微剧透一下兹磁区间覆盖和区间求和的线段树就可以最终解决问题。复杂度 $O((n+q)logn)$ 。

算法4-2

首先还是从右往左处理所有东西。注意到当处理到点 $i$ 的时候，如果存在 $i<j<k$ 使得 $w_j\ge w_k$ 那么我们肯定不可能死在 $k$ 点。

如果把所有这样的点删掉，我们就得到了一个单调栈！然后每次往左扩展一个点就维护一下，询问直接二分就好。注意当删掉一些点以后相当于边权可能会 $>1$ ，加减乘除处理一下就好。 稍微剧透一下你可能需要维护后缀和。复杂度 $O(n+qlogn)$ 。

这两个算法可以通过子任务 $4$ ，或者一些大力出奇迹的算法可能也能过，这样就有 $70$ 分了。

算法五

算法5-1

大致和算法4-1差不多，加上树链剖分和启发式合并的话就能直接做了。代码可能会有一点长。

什么你说不会做？如果能写出4-1的代码，你肯定已经知道了如何往一棵线段树上加一个点更新信息。然后树链剖分以后对于每个点，首先把它的重儿子的线段树拉过来更新一下，然后对于它的每个轻儿子的重链（注意不是轻儿子的子树，否则可能复杂度会多一个log有卡常风险）对应的线段树拉过来更新当前点的线段树就好了。推荐按照树剖的DFS序建一棵线段树，然后上面提到的所有操作都可以在这一棵线段树上做。复杂度 $O((n+q)logn)$ 。

算法5-2

同算法4-2,同样是加上树链剖分和启发式合并搞一搞。复杂度 $O(n+qlogn)$ 。详见xllend3大爷的代码

算法5-?

这题还有很多做法，比如你不喜欢用普通线段树换成动态开点的线段树或者可持久化线段树或者treap什么的也是可以的。当然复杂度和常数就要自己保证了。myy似乎提了一个按权值建LCT的做法：http://matthew99.blog.uoj.ac/blog/2296

数据分块鸡

from jiry_2，数据和题解 from cy

子任务一

设 $f[i]$ 表示最后一个分块点是 $i$ 的最小代价，那么我们转移时可以枚举上一个点 $j$，然后令 $f[i]=min\{f[j]+w(j,i)\}$，其中 $w(l,r)$ 表示与 $[l,r)$ 相交的询问所产生的代价。

时间复杂度：$O(n^{2}q)$。

子任务二

我们可以尝试预处理 $w$ 函数的所有取值。

设 $g[l][r]=w(l,r)$，那么对于一个询问 $[L,R)$, 我们可以根据 $[l,r)$ 与 $[L,R)$ 的相交情况大力讨论一发，拆成把若干个 $g$ 数组的子矩形加上某个数，这可以离线前缀和一下。时间复杂度是 $O(q+n^2)$ 的。

预处理完之后 DP 的复杂度就变成 $O(n^2)$ 了，于是总的复杂度是 $O(q+n^2)$。

子任务四

通过数（da）学（dan）证（cai）明（xiang）我们发现，这个 DP 满足决策单调性。

于是我们可以采用对于满足决策单调性的 DP 的通用做法：在 DP 的同时维护一个单调栈，转移的时候在栈上二分一下得到最优决策点。

计算 $w(l,r)$ 可以通过按照 $[L,R)$ 与 $[l,r)$ 的相交情况分类讨论，拆成对若干个子矩形求和，并用可持久化线段树预处理这些前缀和。

时间复杂度：$O(n{\log }^{2}n)$。

子任务三

通过更进一步的分析，我们可以证明分界点只有可能是 $l_i$，$l_i-1$，$l_i+1$ 或 $r_i$，$r_i-1$，$r_i+1$。因此我们可以只把这些点拿出来 DP。

时间复杂度：$O(q^3)$。

同构判定鸡

from ppfdd，具体想法 from vfleaking，题解也是 vfleaking 写的。

题出得比较仓促，所以测试点只有 $6$ 个……窝先说一下……窝最初的想法是 “哇终于知道怎么出交互式证明的题了！”，然而造题的过程是：

YY 一个图同构算法 → 不会卡 → 再 YY 一个图同构算法 → 还是不会 → 要不咸鱼一下爆搜看看效果如何 → 那不就从构造题变成爆搜题了，不清真 → 继续 YY……

由于我太弱了所以测试点也比较弱，大家玩得开心就好。

卡算法一

算法一：仅检查结点数及边数是否一致。

直接扔个点数边数相同的两个不同构的图就行了，可以获得 $7$ 分。

卡算法二

算法二：首先仅检查结点数及边数，然后结点数很小时使用暴力，否则视为同构。

在卡算法一的基础上造个大一点的图。

卡算法三

算法三：初始每个结点颜色相同，每次对于每个结点结合自身的颜色和周围邻居的颜色编码产生新的颜色，反复迭代直至稳定。将最后每个图所得颜色进行排序，若相同则视为同构。

废话好多！直接扔两个度数相同的图就行了。

卡算法四

算法四：与算法 3 类似，只是用结点间最短距离信息初始化结点颜色。

有两个方法。一个方法是人类智慧构造一下。首先仿照卡算法三的思路，这个图最好是每个结点的距离数组都长得一模一样。那么考虑把大家围成一个圆圈尝试有规律地连边，试了下最后竟然成功了。

A：$6$ 个点，$i$ 与 $(i+1)mod6$ 连边，$i$ 与 $(i+3)mod6$ 连边。

B：$6$ 个点，$i$ 与 $(i+2)mod6$ 连边，$i$ 与 $(i+3)mod6$ 连边。

这样构造发现恰好是满足的，就可以同时卡掉算法一二三四了。

还有另一个构造，方法是找两个不同构且每个点度数都相同的图，分别新建一个点向所有点连边。这样其实原图中没有边相连的两个点距离就为 $2$，有边即为 $1$。这样的构造也是可以骗过算法四的。

另一个方法：大爆搜所有无向图，搜到 $n=6$ 就能找到上面的这个构造了……

卡算法五

算法五：枚举一个图中的一个固定的结点与另一个图中哪个结点对应，将他们分别染成特殊的颜色，其它结点颜色照常初始化，再用算法 3 中的迭代。若存在一种对应使得最后所得颜色相同，则视为同构。

只用在卡算法四的基础上往前面插入一个编号为 1 号点向所有其他点连边就行了，这样给这个点特殊染色不会带来任何信息。

另一个方法：大爆搜所有无向图，搜到 $n=7$ 就能找到上面的这个构造了……

卡算法六

算法六：一种基于邻接矩阵的整数次幂的迹的哈希算法

啊发现哈希好难卡……发现哈希的模数是 int 范围的。考虑用爆搜来构造。

但是要怎么快速生成很多个满足前 5 个算法的图呢？

可以这样想：算法五里引入的这个向所有点连边的点不会带来任何信息，所以多加几个这样的点也肯定满足题目条件。而且进一步考虑在这样的新点之间连边，如果连边方式一致，那么同样也不会给那个 $6$ 点图带来任何信息。

所以我们可以在卡算法四的基础上，给 $A,B$ 加一大堆新点出来，然后随机连边。但是这样大约需要随机 $O(M)$ 次才能随机到相同的哈希值。

这个哈希函数实在是算得太慢了，GG 怎么办呢。如果用生日攻击的话，那么模数是 $M$ 期望 $O(\sqrt{M})$ 个样本就能卡了。

然而我们可以结合卡算法四中的第二个构造。把新点随机成点度数相等的图就好了。由于 $A,B$ 不同构所以我们可以直接随机不用判断是否随机到了同构的图。

当然场上有一位机智 bzoj 给出了一个直接的构造：在这里 太强了……QAQ……

终极武器

好吧虽然不是想鼓励大家这样做，但是可能很有效。上网搜“graph isomorphism counter example”，可以得到一些奥妙重重的卡图同构算法的反例。下载一些下来喂进交互库说不定哪个就成功了。囧rz……以后出题还是要注意注意别出这种能 google 的题。

嗨呀以及感觉这次的题目总体还是偏难，感谢大家参赛啦！