【APIO2025】排列游戏 - 题目 - Universal Online Judge

Alice 和 Bob 是童年时代的朋友，他们喜欢玩智力游戏。今天，他们在玩一个关于图的新游戏。

游戏中包含一个连通图，具有 $m$ 个顶点，编号为 $0$ 到 $m - 1$ ，以及 $e$ 条边，编号为 $0$ 到 $e - 1$ 。第 $i$ 条边连接顶点 $u [i]$ 和 $v [i]$ 。

游戏中还包含一个长度为 $n$ 的排列 $p [0], p [1], \dots, p [n - 1]$ ，其中 $m \leq n$ 。排列是一个数组，其中从 $0$ 到 $n - 1$ 的每个数字以某种顺序仅出现一次。排列 $p$ 的分数是满足 $p [i] = i$ 的下标 $i$ 的数量。

游戏最多持续 $10^{100}$ 个回合。在每个回合中，都会发生以下情况：

如果 Alice 决定结束游戏，游戏终止。
否则，Alice 选择一组两两不同的下标 $t [0], t [1], \dots, t [m - 1]$ ，满足 $0 \leq t [i] < n$ 。请注意，游戏不要求 $t [0] < t [1] < \dots < t [m - 1]$ 。
Bob 选择一个图中边的下标 $0 \leq j < e$ ，并交换 $p [t [u [j]]]$ 和 $p [t [v [j]]]$ 。

Alice 希望能最大化排列的最终分数而 Bob 希望最小化排列的最终分数。

你的任务是帮助 Alice，与由评测程序模拟的 Bob 进行游戏。

定义一局游戏的“最优分数”为当 Alice 和 Bob 都采用最优策略进行游戏时最终得到的排列的分数。

你需要求出本局游戏的最优分数，然后与 Bob 进行游戏，且需要在若干轮后至少达到最优分数。

请注意：你实现的 Alice 的策略应当是普适性的，能够处理 Bob 可能采用的各种策略，即使 Bob 采用的策略可能并非最优。

你要实现以下函数：

int Alice(int m, int e, std::vector<int> u, std::vector<int> v, int n, std::vector<int> p)

该函数恰好被调用一次。该函数应该返回一个整数，即游戏的最后分数，假设 Alice 和 Bob 都以最优策略玩游戏。

在该函数中，你可以调用以下函数：

int Bob(std::vector<int> t)

t: 长度为 $m$ 的数组，包含一组两两不同的下标，满足 $0 \leq t [i] < n$ 且对于任意 $i \neq j$ 均有 $t [i] \neq t [j]$ 。
该函数返回一个整数 $j$ ，满足 $0 \leq j < e$ 。
该函数可以被调用多次。

考虑以下调用：

Alice(5, 6, [4, 0, 3, 1, 4, 2], [2, 2, 0, 2, 0, 3], 10, [8, 2, 7, 6, 1, 5, 0, 9, 3, 4])

如下图所示：

$p$ 的初值为 $[8, 2, 7, 6, 1, 5, 0, 9, 3, 4]$ 。

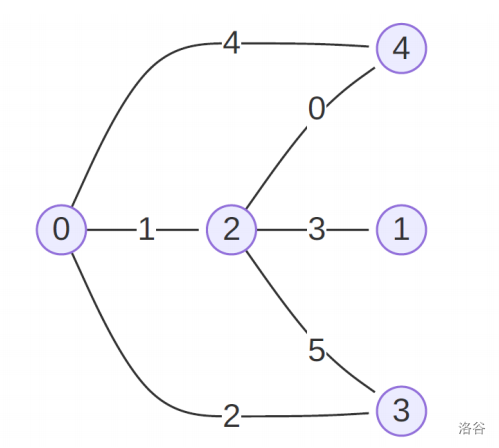
给定以上约束条件，我们可以证明排列的最优分数为 1。

假设，Alice 做了以下 4 次操作：

给 Bob 的参数 $t$	Bob 返回的值	$p$ 对应的下标	Bob 交换后的 $p$
[3, 1, 5, 2, 0]	5	5, 2	[8, 2, 5, 6, 1, 7, 0, 9, 3, 4]
[9, 3, 7, 2, 1]	0	1, 7	[8, 9, 5, 6, 1, 7, 0, 2, 3, 4]
[5, 6, 7, 8, 9]	1	5, 7	[8, 9, 5, 6, 1, 2, 0, 7, 3, 4]
[7, 5, 2, 3, 6]	3	5, 2	[8, 9, 2, 6, 1, 5, 0, 7, 3, 4]

注意 Alice 和 Bob 所做的操作不一定是最优的。上面显示的操作纯粹是为了演示。另外，注意到 Alice 实际上可以在一开始就结束游戏，因为最开始的排列分数已经达到了最优分数 1。

在 Alice 做了上述所有操作后，排列的实际分数为 $3$ （ $p [2] = 2$ , $p [5] = 5$ , $p [7] = 7$ ）。

函数 Alice() 最后返回值为 1，即排列的最优分数。

请注意，即使 Alice 通过与 Bob 玩游戏获得了分数 3，但如果函数 Alice() 的返回值是 3 而不是 1，你将获得 0 分。

图是连通的，并且没有自环和重边。 $p$ 是一个排列，即对任意 $i \neq j$ , $p [i] \neq p [j]$ 。

对于每个子任务，你可以获得部分分数。设 $r$ 是 $\frac{k}{n}$ 在某个子任务的所有测试用例中的最大比值，其中 $k$ 是回合数（即对 Bob() 的调用次数）。那么，你在该子任务的得分为该子任务的满分乘以以下数字：

特别地，如果在 $3 n$ 个回合内解决问题，则该子任务将获得满分。使用超过 $12 n$ 个回合将导致该子任务获得 0 分（显示为 output isn't correct）。

评测程序示例按以下格式读取输入：

评测程序示例按以下格式打印你的答案：

Universal Online Judge