斯芬克斯为你准备了一个谜题。给定 $N$ 个顶点的图，顶点从 $0$ 到 $N-1$ 编号。图中有 $M$ 条边，从 $0$ 到 $M-1$ 编号。每条边连接两个不同的顶点，且边是双向的。具体来说，对从 $0$ 到 $M-1$ 的每个 $j$，边 $j$ 连接顶点 $X[j]$ 和 $Y[j]$。任意两个顶点之间最多有一条边。若两个顶点被一条边连接，则它们是相邻的。

对顶点序列 $v_0,v_1,\dots ,v_k$（对 $k\ge 0$），若每两个连续顶点 $v_l$ 和 $v_{l+1}$（对所有满足 $0\le l<k$ 的 $l$）是相邻的，则称其为一条路径。路径 $v_0,v_1,\dots ,v_k$ 连接顶点 $v_0$ 和 $v_k$。在给定的图中，每对顶点被某条路径连接。

现在有 $N+1$ 种颜色，从 $0$ 到 $N$ 编号。其中，颜色 $N$ 是特殊的，称为斯芬克斯之色。一开始每个顶点都有一种颜色，顶点 $i$（$0\le i<N$）的颜色是 $C[i]$。多个顶点可以是同一种颜色的，有的颜色可能没有对应的顶点，且不会有顶点的颜色是斯芬克斯之色。也就是说，$0\le C[i]<N$（$0\le i<N$）。

若一条路径 $v_0,v_1,\dots ,v_k$（对 $k\ge 0$）上的所有顶点都是相同颜色的，则称其是单色的。也就是说，满足 $C[v_l]=C[v_{l+1}]$（对所有满足 $0\le l<k$ 的 $l$）。此外，两个顶点 $p$ 和 $q$（$0\le p<N$，$0\le q<N$）在同一个单色分支中，当且仅当它们被某条单色路径连接。

你知道图中顶点和边的关系，但是你不知道每个顶点的颜色。你希望通过重新着色实验来弄清楚顶点的颜色。

在一次重新着色实验中，你可以对任意多的顶点进行重新着色。具体来说，在一次重新着色实验中，你先给出一个长度为 $N$ 的数组 $E$，对每个 $i$（$0\le i<N$），$E[i]$ 的值在 $-1$ 和 $N$ 之间（包括 $-1$ 和 $N$）。重新着色后，每个顶点 $i$ 的颜色变成了 $S[i]$，其中 $S[i]$ 的值： 若 $E[i]=-1$，则是 $C[i]$，也就是重新着色前顶点 $i$ 的颜色； 否则，是 $E[i]$。

注意：你可以在重新着色的过程中使用斯芬克斯之色。

在将每个顶点 $i$ 的颜色设为 $S[i]$（$0\le i<N$）之后，斯芬克斯会宣布图中单色分支的数量。新的着色情况仅在本次重新着色实验中有效，因此当本次实验结束后，所有顶点的颜色会恢复成最初的情况。

你的任务是至多通过 $2750$ 次重新着色实验来确定图中顶点的颜色。如果正确给出了每对相邻顶点是否具有相同颜色，那么也会获得部分分数。

实现细节

你要实现以下函数。

std::vector<int> find_colours(int N,
    std::vector<int> X, std::vector<int> Y)

• $N$：图中顶点的数量。
• $X$，$Y$：两个长度为 $M$ 的数组，描述图中的边。
• 该函数应该返回一个长度为 $N$ 的数组 $G$，表示图中顶点的颜色。
• 对每个测试用例，该函数恰好被调用一次。

以上函数可以通过调用下面的函数来进行重新着色实验：

int perform_experiment(std::vector<int> E)

• $E$：长度为 $N$ 的数组，指定顶点重新着色的方式。
• 该函数返回根据 $E$ 所给出的方式进行重新着色后单色分支的数量。
• 该函数至多只能调用 $2750$ 次。

评测程序不是自适应的。也就是说，顶点的颜色在调用 find_colours 之前就已经固定下来了。

约束条件

• $2\le N\le 250$
• $N-1\le M\le \frac{N\cdot (N-1)}{2}$
• 对所有满足 $0\le j<M$ 的 $j$，都有 $0\le X[j]<Y[j]<N$。
• 对所有满足 $0\le j<k<M$ 的 $j$ 和 $k$，都有 $X[j]\ne X[k]$ 或 $Y[j]\ne Y[k]$。
• 每对顶点被某条路径连接。
• 对所有满足 $0\le i<N$ 的 $i$，都有 $0\le C[i]<N$。

子任务

在每个子任务中，如果你的程序正确给出了每对相邻顶点是否具有相同颜色，那么也会获得部分分数。

更准确地说，如果在所有测试用例中 find_colours 返回的数组 $G$ 与数组 $C$ 完全一样（也就是对所有满足 $0\le i<N$ 的 $i$，都有 $G[i]=C[i]$），你会获得该子任务的全部分数。否则，如果在某个子任务的所有测试样例中满足下列条件，你会获得该子任务 $50\mathrm{\%}$ 的分数：

• 对所有满足 $0\le i<N$ 的 $i$，都有 $0\le G[i]<N$；
• 对所有满足 $0\le j<M$ 的 $j$，都有：
  • $G[X[j]]=G[Y[j]]$ 当且仅当 $C[X[j]]=C[Y[j]]$。

例子

考虑以下函数调用。

find_colours(4, [0, 1, 0, 0], [1, 2, 2, 3])

在这个例子中，假设顶点的（隐藏的）颜色是 $C=[2,0,0,0]$，如下图所示。顶点的颜色同时也用数字标注在顶点右上角的标签里。

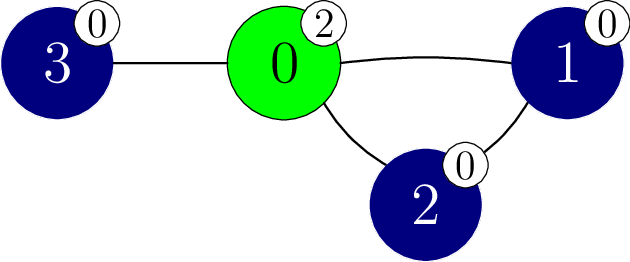
假设该函数以下列方式调用 perform_experiment。

perform_experiment([-1, -1, -1, -1])

这次调用没有重新着色任何顶点，因此所有顶点都保持它们原来的颜色。

顶点 $1$ 和顶点 $2$ 都是颜色 $0$ 的。因此路径 $1,2$ 是单色路径，从而顶点 $1$ 和顶点 $2$ 在同一个单色分支中。

顶点 $1$ 和顶点 $3$ 都是颜色 $0$ 的。但是由于不存在连接它们的单色路径，因此它们在不同的单色分支中。

总共有 $3$ 个单色分支，分别是顶点集合 $\{0\}$、$\{1,2\}$ 和 $\{3\}$。因此，本次函数调用返回 $3$。

再假设该函数以下列方式调用 perform_experiment。

perform_experiment([0, -1, -1, -1])

这次调用只把顶点 $0$ 重新着色成颜色 $0$，结果如下图所示。

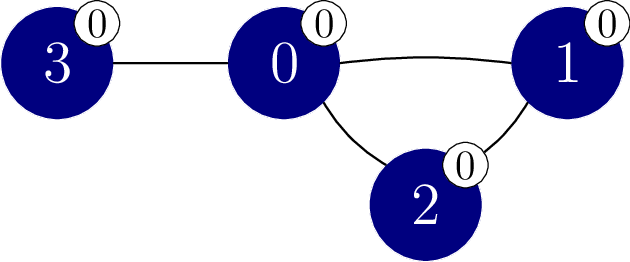
此时所有顶点都属于同一个单色分支，因此本次函数调用返回 $1$。由此可以推断顶点 $1$、$2$ 和 $3$ 都是颜色 $0$ 的。

假设该函数还以下列方式调用 perform_experiment。

perform_experiment([-1, -1, -1, 2])

这次调用把顶点 $3$ 重新着色成颜色 $2$，结果如下图所示。

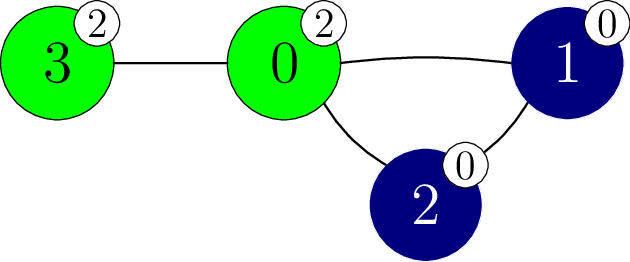
这时有 $2$ 个单色分支，分别是顶点集合 $\{0,3\}$ 和 $\{1,2\}$，因此本次函数调用返回 $2$。由此可以推断顶点 $0$ 是颜色 $2$ 的。

然后函数 find_colours 返回数组 $[2,0,0,0]$。由于 $C=[2,0,0,0]$，因此可以获得满分。

此外，也还有多种返回值，例如 $[1,2,2,2]$ 或 $[1,2,2,3]$，可以获得 $50\mathrm{\%}$ 的分数。

评测程序示例

输入格式：

N  M
C[0]  C[1] ... C[N-1]
X[0]  Y[0]
X[1]  Y[1]
...
X[M-1]  Y[M-1]

输出格式：

L  Q
G[0]  G[1] ... G[L-1]

这里，$L$ 是 find_colours 返回的数组 $G$ 的长度，$Q$ 是调用 perform_experiment 的次数。

时间限制：$\mathtt{\text{1.5s}}$

空间限制：$\mathtt{\text{2048MB}}$