“为什么要攀登？因为山就在那里。”

慕士塔格山上有 $n$ 处点位，点从 $1$ 到 $n$ 编号，$1$ 号点位为山顶。这 $n$ 个点位构成一棵有根树的结构，其中 $1$ 号点位为根，对于 $2\le i\le n$，$i$ 号点位的父亲结点为 $p_i$ 号点位。

记 $d_i$ 为 $i$ 号点位到山顶所需经过的边数。形式化地说，$d_1=0$，对于 $2\le i\le n$，$d_i=d_{p_i}+1$。

定义一条登山路径为从 $2\sim n$ 号点位中的某一个开始，经过若干次移动后到达山顶的方案。

定义一次从 $i(2\le i\le n)$ 号点位出发的移动为以下两种方式之一：

1. 冲刺：在给定的冲刺范围 $[l_i,r_i]$ 内，选择一个正整数 $k$ 满足 $l_i\le k\le r_i$，向山顶移动 $k$ 步，即移动至 $i$ 号点位在有根树上的 $k$ 级父亲处。保证 $1\le l_i\le r_i\le d_i$。
2. 休息：由于慕士塔格山地形陡峭，休息时会滑落到某一个儿子结点处。形式化地说，选择一个满足 $p_j=i$ 的 $j$，移动至到 $j$ 号点位。特别地，若 $i$ 号点位为有根树的叶子结点，则不存在满足 $p_j=i$ 的 $j$，因此此时不能选择休息。

定义一条登山路径对应的登山序列为初始点位以及每次移动到的点位所构成的序列。形式化地说，一条从 $x$ 号点位开始的登山路径对应的登山序列是一个点序列 $a_1=x,a_2,\dots ,a_m=1$ 满足对于 $1\le i<m$，$a_{i+1}$ 是 $a_i$ 的 $k(l_{a_i}\le k\le r_{a_i})$ 级祖先或 $p_{a_{i+1}}=a_i$。

为了保证每次冲刺都能更接近山顶，一条合法的登山路径需要满足：对于初始点位或某次移动到的点位 $i$，以后冲刺到的点位 $j$ 都必须满足 $d_j<d_i-h_i$，其中 $h_i$ 是一个给定的参数，保证 $0\le h_i<d_i$。形式化地说，一条合法的登山路径对应的登山序列 $a_1,a_2,\dots ,a_m$ 需要满足：对于所有 $1\le i<j\le m$，若 $p_{a_j}\ne a_{j-1}$，则 $d_{a_j}<d_{a_i}-h_{a_i}$。

对于 $2\sim n$ 号所有点位，求从这些点位开始的合法的登山路径条数。两条登山路径不同当且仅当其对应的登山序列不同。由于答案可能较大，你只需要求出答案对 $998244353$ 取模后的结果。

输入格式

本题有多组测试数据。

输入的第一行包含一个整数 $c$，表示测试点编号。$c=0$ 表示该测试点为样例。如果你要提交 hack 数据，请你保证 $c=0$。

输入的第二行包含一个整数 $t$，表示测试数据组数。

接下来依次输入每组测试数据，对于每组测试数据：

输入的第一行包含一个整数 $n$，表示慕士塔格山的点位数量。

接下来 $n-1$ 行，第 $i-1(2\le i\le n)$ 行包含四个整数 $p_i,l_i,r_i,h_i$。保证 $1\le p_i<i$，$1\le l_i\le r_i\le d_i$，$0\le h_i<d_i$。

输出格式

对于每组测试数据，输出一行 $n-1$ 个整数，分别表示从点位 $2\sim n$ 到达山顶的方案数对 $998244353$ 取模后的结果。

样例一

input

0
3
5
1 1 1 0
2 1 1 0
2 1 2 1
4 2 3 0
6
1 1 1 0
2 1 2 0
3 1 3 2
4 1 4 1
5 1 5 3
6
1 1 1 0
2 1 2 0
2 1 2 0
3 1 2 0
3 2 3 2

output

3 3 2 4
5 9 3 21 6
4 10 5 14 1

explanation

样例 $1$ 共包含三组测试数据。

对于第一组测试数据，慕士塔格山的点位结构如下：

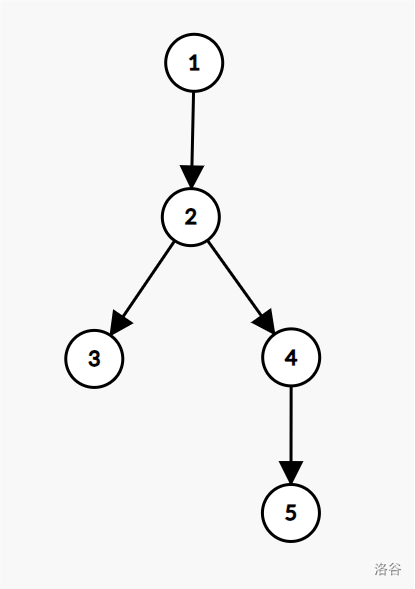
在该测试数据中，$d_1=0$，$d_2=1$，$d_3=d_4=2$，$d_5=3$。

从 $4$ 开始的合法的登山路径共有以下 $2$ 条：

1. 直接选择冲刺到 $4$ 的 $2$ 级父亲，也就是 $1$，到达山顶，对应的登山序列为 $[4,1]$。
2. 先休息滑落到 $5$；然后从 $5$ 冲刺到它的 $3$ 级父亲，到达山顶。对应的登山序列为 $[4,5,1]$。

从 $5$ 开始的合法的登山路径共有以下 $4$ 条：

1. 直接选择冲刺到 $5$ 的 $3$ 级父亲，也就是 $1$，到达山顶。对应的登山序列为 $[5,1]$。
2. 先冲刺到 $5$ 的 $2$ 级父亲，也就是 $2$；然后再从 $2$ 冲刺到它的 $1$ 级父亲，到达山顶。对应的登山序列为 $[5,2,1]$。
3. 先冲刺到 $5$ 的 $2$ 级父亲，也就是 $2$；然后在 $2$ 处休息，滑落到 $4$；接着从 $4$ 冲刺到它的 $2$ 级父亲，到达山顶。对应的登山序列为 $[5,2,4,1]$。
4. 先冲刺到 $5$ 的 $2$ 级父亲，也就是 $2$；然后在 $2$ 处休息，滑落到 $4$；继续休息，滑落到 $5$；接着从 $5$ 再次冲刺到它的 $3$ 级父亲，到达山顶。对应的登山序列为 $[5,2,4,5,1]$。

样例二

见附件下载中的 ex_mountain2.in 与 ex_mountain2.ans。

这个样例满足测试点 $2,3$ 的约束条件。

样例三

见附件下载中的 ex_mountain3.in 与 ex_mountain3.ans。

这个样例满足测试点 $9$ 的约束条件。

样例四

见附件下载中的 ex_mountain4.in 与 ex_mountain4.ans。

这个样例满足测试点 $11,12$ 的约束条件。

样例五

见附件下载中的 ex_mountain5.in 与 ex_mountain5.ans。

这个样例满足测试点 $13$ 的约束条件。

数据范围

对于所有测试数据保证：$1\le t\le 4$，$2\le n\le {10}^5$。

对于任意的 $2\le i\le n$，保证：$1\le p_i<i$，$1\le l_i\le r_i\le d_i$，$0\le h_i<d_i$。

时间限制：$\cancel{2\mathtt{\text{s}}}4\mathtt{\text{s}}$

空间限制：$2\mathtt{\text{GB}}$