跳蚤国王兴致大发，在刚建好的跳蚤利亚上游玩！

跳蚤利亚共有 $n$ 个城市，彼此之间连接着 $n-1$ 条双向道路，而且这些道路确保了城市间的互通。在这些城市中，有 $m$ 个被誉为著名的旅游景点。为了探索这些城市的风光，跳蚤国王决定从一号城市（皇宫）出发，途经一些城市，最终回到皇宫。跳蚤国王希望能经过每个旅游景点至少一次。

跳蚤国王拥有强大的跳跃能力，可以一次性跳过一条或两条道路。但是，一次性跳过两条道路会消耗大量体力，因此这种跳跃的次数不能超过 $k$ 次。

为了合理规划行程，跳蚤国王需要进行 $q$ 次询问。每次询问中，他会提供一个 $k$ 值，你需要回答在给定 $k$ 的情况下，跳蚤国王至少需要跳跃几次才能完成整个旅程。

输入格式

本题有多组测试数据。

第一行一个整数 $T$，表示测试数据组数。

对于每组测试数据：

• 第一行三个整数 $n,m,q$。
• 后 $(n-1)$ 行每行两个整数 $u,v$，表示城市间的道路。
• 后一行 $m$ 个整数 $a_1,a_2,\dots ,a_m$，表示旅游景点对应的城市编号。
• 后一行 $q$ 个整数 $k$。

输出格式

对于每组测试数据：

• 一行 $q$ 个整数，表示每个询问的答案。

样例一

input

3
5 2 2
1 2
2 3
3 4
4 5
3 5
0 2
5 2 2
1 2
1 3
2 4
2 5
4 5
0 2
5 4 2
1 2
2 3
1 4
4 5
2 3 4 5
0 4

output

8 6
6 4
8 5

explanation

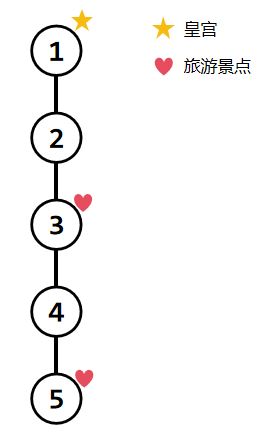
对于第一组测试数据，跳蚤利亚的结构如下图所示：

• $k=0$ 时的一种跳跃方式为 $1\to 2\to 3\to 4\to 5\to 4\to 3\to 2\to 1$。
• $k=2$ 时的一种跳跃方式为 $1\to 3\to 5\to 4\to 3\to 2\to 1$。

样例二

见下发文件。该样例满足子任务 7 的限制。

限制与约定

本题采用捆绑测试。

• Subtask 1（5 points）：$n=3$。
• Subtask 2（5 points）：$k=0$。
• Subtask 3（5 points）：$m=1$。
• Subtask 4（10 points）：$T\le 10$，$q\le 10$，$m\le 8$。
• Subtask 5（10 points）：$T\le 10$，$q\le 10$，$m\le 15$。
• Subtask 6（10 points）：保证任意一个城市最多与两个城市相连。
• Subtask 7（10 points）：$q=1$。
• Subtask 8（15 points）：$n,\sum n\le {10}^3$。
• Subtask 9（30 points）：无特殊限制。

对于 $100\mathrm{\%}$ 的数据，$1\le T\le {10}^5$，$3\le n,\sum n\le {10}^5$，$1\le q,\sum q\le {10}^5$，$1\le m<n$，$0\le k\le {10}^9$，$1\le u,v\le n$，$2\le a_i\le n$，保证每组测试数据中的 $a_i$ 互不相同。

时间限制：$\mathtt{\text{1s}}$

空间限制：$\mathtt{\text{512MB}}$