如果一个无向连通图的任意一条边最多属于一个简单环，我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。

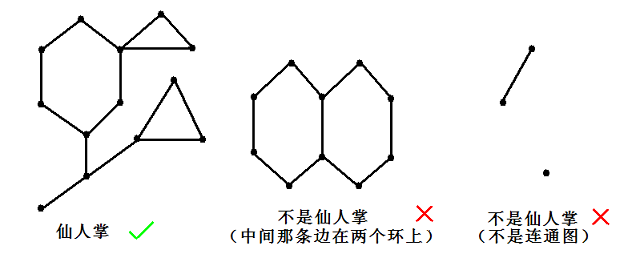
现给定一棵仙人掌，每条边有一个正整数权值，每次给 $k$ 个点（可以存在相同点），问从它们中选出两个点（可以相同），它们之间最短路的最大值是多少。

输入格式

第一行两个非负整数 $n,m$，表示仙人掌的点数和边数。

接下来 $m$ 行，每行三个正整数 $v,u,w$ $(1\le v,u\le n)$，表示 $v$ 与 $u$ 之间有一条边权为 $w$ 的无向边。点从 $1$ 开始编号。

保证输入的图是一棵仙人掌，保证没有自环，但可能有重边。

接下来一行一个非负整数 $Q$，表示询问个数。

接下来 $Q$ 行每行第一个数是正整数 $\mathrm{cnt}$ 表示点数，接下来 $\mathrm{cnt}$ 个数表示给定的点。

输出格式

对每个询问输出一个数，表示该询问对应的最大值。

样例一

input

10 14
10 7 1
3 8 7
1 6 9
7 2 10
8 9 9
1 7 1
8 5 2
4 5 4
1 7 4
2 9 8
9 3 3
8 4 2
1 6 5
7 9 10
6
2 9 5
2 8 10
3 8 7 6
2 6 4
3 3 4 2
1 10

output

11
20
25
27
19
0

explanation

前五个询问的答案路径分别为(如果有重边则显然走较短的边):

$9\to 8\to 5$

$8\to 9\to 7\to 10$

$8\to 9\to 7\to 1\to 6$

$4\to 8\to 9\to 7\to 1\to 6$

$2\to 9\to 8\to 4$

最后一个询问的答案显然是$0$。

限制与约定

边权不超过 $2^{31}-1$。

$\mathrm{tot}$ 表示询问的总点数。

对于 5% 的数据，$n,\mathrm{tot}\le 7$。

对于 10% 的数据，$n,\mathrm{tot}\le 5000$。

对于另外 10% 的数据，$Q\le 10$，其中存在 $Q\le 2$ 的数据。

对于另外 30% 的数据，$m=n-1$。

对于 100% 的数据，$n,\mathrm{tot}\le 300000$。

此外为了照顾被卡常数的同学，本题存在过渡数据。

时间限制：$5\mathtt{\text{s}}$

空间限制：$512\mathtt{\text{MB}}$

来源

matthew99

题解

https://matthew99.blog.uoj.ac/blog/241

下载

样例数据下载