水羊羹是一种用红豆沙制成的日式点心，将红豆沙与琼脂混合，并用矩形模具定型，这样就可以做成水羊羹了。

现在 JOI 君有一台水羊羹机器。使用它，JOI 君可以制作一个横向的矩形水羊羹，其上有 $N-1$ 条垂直切割线。水羊羹的长度和切割线位置由机器上设置的 $N$ 个参数 $d_1,d_2,\dots ,d_N$ 确定。水羊羹的长度为 $d_1+d_2+\dots +d_N$。从左到右第 $(i-1)(1\le i\le N)$ 条切割线与第 $i$ 条切割线之间的距离为 $d_i$。这里，我们考虑水羊羹的最左边为第 $0$ 条切割线，水羊羹的最右边为第 $N$ 条切割线。最初，水羊羹机器的参数满足 $d_i=L_i(1\le i\le N)$。

JOI 君计划组织 $Q$ 次茶会。第 $j(1\le j\le Q)$ 次茶会由整数 $X_j,Y_j,A_j,B_j$ 表示。茶会按如下方式进行：

1. 水羊羹机器的参数 $d_{X_j}$ 被更新，并设置为 $Y_j$
2. JOI 君用水羊羹机器只做了一个新的水羊羹。他把水羊羹在第 $A_j$ 条切割线和第 $B_j$ 条切割线之间的部分取出，用于茶会。他吃掉了剩余部分。
3. JOI 君沿一些切割线来切为茶会准备的水羊羹。他会将水羊羹切为一或更多块。在这个过程中应满足以下条件：如果这些切好的水羊羹块按最初的位置从左到右排列，那么这些水羊羹块的长度序列应该是锯齿形的。

这里，如果序列中元素交替上升和下降，就称这个序列是锯齿形的。例如，序列 $(2,9,2,7),(7,1,9,4,6),(5),(2,1)$ 是锯齿形的，但序列 $(1,2,3),(7,1,4,4,6),(2,2)$ 不是锯齿形的。准确地说，一个序列 $(x_1,x_2,\dots ,x_m)$ 被称为锯齿形的，当且仅当以下条件中至少一个被满足：

• 对于 $k=1,2,\dots ,m-1$，当 $k$ 为奇数时满足不等式 $x_k<x_{k+1}$，当 $k$ 为偶数时满足不等式 $x_k>x_{k+1}$。
• 对于 $k=1,2,\dots ,m-1$，当 $k$ 为奇数时满足不等式 $x_k>x_{k+1}$，当 $k$ 为偶数时满足不等式 $x_k<x_{k+1}$。

因为 JOI 君想要把水羊羹给尽可能多的朋友们，他想最大化步骤 $3$ 中得到的水羊羹数。

给定初始水羊羹机器的参数和茶会计划，写一个程序计算对于每次茶会，在满足条件的情况下最多能得到的最大水羊羹数。注意，在本题的限制下，满足条件的水羊羹切分方法必然存在。

输入格式

第一行一个整数 $N$。

第二行 $N$ 个整数 $L_1,L_2,\dots ,L_N$，

第三行一个整数 $Q$。

接下来 $Q$ 行，每行四个整数 $X_j,Y_j,A_j,B_j$。

输出格式

输出 $Q$ 行，第 $j$ 行输出对于第 $j$ 次茶会，在满足条件的情况下最多能得到的最大水羊羹数。

样例输入 1

6
5 6 8 7 4 9
1
6 9 0 5

样例输出 1

3

在第一场茶会，水羊羹机器的参数被设为 $(d_1,d_2,d_3,d_4,d_5,d_6)=(5,6,8,7,4,9)$。JOI 君使用第 $0$ 条和第 $5$ 条切割线之间的部分，如下图所示。

JOI 君可以按如下方案切割水羊羹。

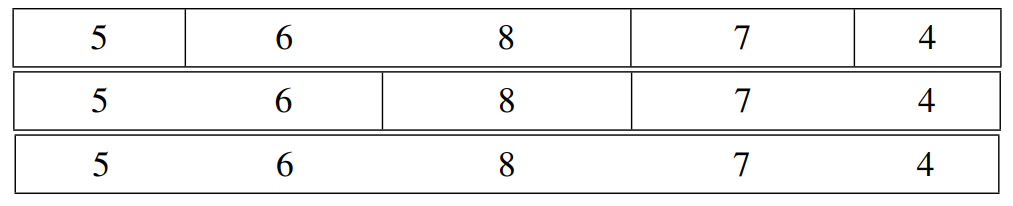
在第一种方案中，水羊羹块的长度为 $5,14,7,4$。因为这个序列不是锯齿形的，所以它不符合要求。在第二种方案中，水羊羹块的长度为 $11,8,11$。因为这个序列是锯齿形的，所以它符合要求。在第三种方案中，水羊羹块的长度为 $30$。因为这个序列是锯齿形的，所以它符合要求。

如果 JOI 君使用方法 $2$ 切割水羊羹的话，他会得到 $3$ 块。因为他不可能在满足要求的同时切出 $4$ 块及以上水羊羹，所以第一行输出 $3$。

这组样例满足所有子任务的限制。

样例输入 2

4
6 2 3 6
3
3 2 1 3
4 5 1 4
1 1 0 4

样例输出 2

1
2
3

在第一个茶会中，茶会上使用的羊羹长度为 $4$，其上有一条切割线，距离最左端的长度为 $2$。如果 JOI 君不切割，直接使用这块水羊羹的话，他会得到一块水羊羹。这个长度序列为 $(4)$，是锯齿形的。因为他不可能获得一个以上的水羊羹块，所以输出 $1$。

在第二个茶会中，茶会上使用的羊羹长度为 $9$，其上有两条切割线，距离最左端的长度分别为 $2,4$。如果 JOI 君沿距离最左端长度为 $4$ 的切割线切割的话，他会得到两块水羊羹，长度序列为 $(4,5)$，是锯齿形的。因为他不可能获得两个以上的水羊羹块，所以输出 $2$。

在第三个茶会中，茶会上使用的羊羹长度为 $10$，其上有三条切割线，距离最左端的长度分别为 $1,3,5$。如果 JOI 君沿距离最左端长度为 $3$ 和 $5$ 的切割线切割的话，他会得到三块水羊羹，长度序列为 $(3,2,5)$，是锯齿形的。因为他不可能获得三个以上的水羊羹块，所以输出 $3$。

这组样例满足子任务 $1,2,3,5,6$ 的限制。

数据范围

对于所有输入数据，满足：

• $1\le N\le 2.5\times {10}^5$
• $1\le L_i\le {10}^9$
• $1\le Q\le 5\times {10}^4$
• $1\le X_j\le N,1\le Y_j\le {10}^9$
• $0\le A_j<B_j\le N$

详细子任务附加限制及分值如下表所示。

时间限制：3s

空间限制：1024MB