给定一张带权简单无向图，请输出这张图从 $S$ 到 $T$ 的最小割的个数。

从 $S$ 到 $T$ 的割即一个原图中的边的子集，使得去掉这些边后图中不存在从编号为 $S$ 的结点到编号为 $T$ 的结点的路径。一个 $S$ 到 $T$ 的割的权值即这些边的权值之和。从 $S$ 到 $T$ 的最小割即从 $S$ 到 $T$ 的割中权值最小的。

你只用输出答案对 $998244353$ （$7\times 17\times 2^{23}+1$，一个质数）取模后的结果。

输入格式

该题为提交答案型试题，所有输入数据 mincut1.in ~ mincut10.in 见输入数据下载。

输入文件的第一行包含四个整数 $n,m,S,T$。$n$ 和 $m$ 分别表示这张图的点数和边数。保证 $1\le S,T\le n$。

接下来 $m$ 行，每行三个正整数 $x,y,z$，代表第 $x$ 个点和第 $y$ 个点之间有一条权值为 $z$ 的无向边。

输出格式

针对给定的 10 个输入文件 mincut1.in ~ mincut10.in，你需要分别提交你的输出文件 mincut1.out ~ mincut10.out。

输出文件只包含一个正整数，代表这张无向图从 $S$ 到 $T$ 的最小割的个数。

样例一

input

4 4 1 4
1 2 1
2 3 1
1 3 1
3 4 2

output

3

explanation

从 $1$ 到 $4$ 的三种最小割如下图所示：

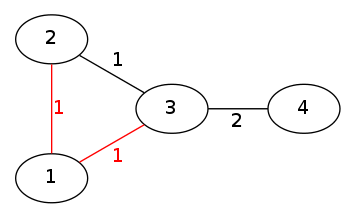
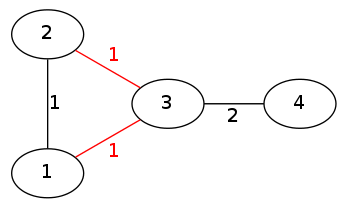
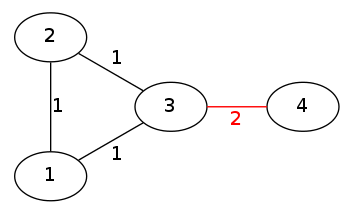
来源

PoPoQQQ

下载

输入数据下载