题目描述
Vétyem Woods 是一片著名的缤纷多彩的森林。其中最老最高的一棵山毛榉树叫 Ős Vezér。
树 Ős Vezér 可以被建模成 $N$ 个结点和 $N-1$ 条边的集合。结点的编号为从 $0$ 到 $N-1$，边的编号为从 $1$ 到 $N-1$。每条边均连接树上两个不同的结点。具体地说，边 $i$（$1 \le i \lt N$）从结点 $i$ 连接到结点 $P[i]$，这里 $0 \le P[i] \lt i$。结点 $P[i]$ 被称为是结点 $i$ 的父结点，而结点 $i$ 被称为是结点 $P[i]$ 的一个子结点。
每条边都有某种颜色。一共有 $M$ 种可能的颜色，编号为从 $1$ 到 $M$。边 $i$ 的颜色为 $C[i]$。不同的边可能有相同的颜色。
注意，在上面的定义中，$i = 0$ 的情形并不对应树上的边。方便起见，我们令 $P[0] = -1$ 和 $C[0] = 0$。
例如，假定 Ős Vezér 有 $N = 18$ 个结点和 $M = 3$ 种可能的颜色，以及 $17$ 条边。边的描述为 $P = [-1, 0, 0, 0, 1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 5, 10, 11, 11]$，边的颜色为 $C = [0, 1, 2, 3, 1, 2, 3, 1, 3, 3, 2, 1, 1, 2, 2, 1, 2, 3]$。这棵树如下图所示：
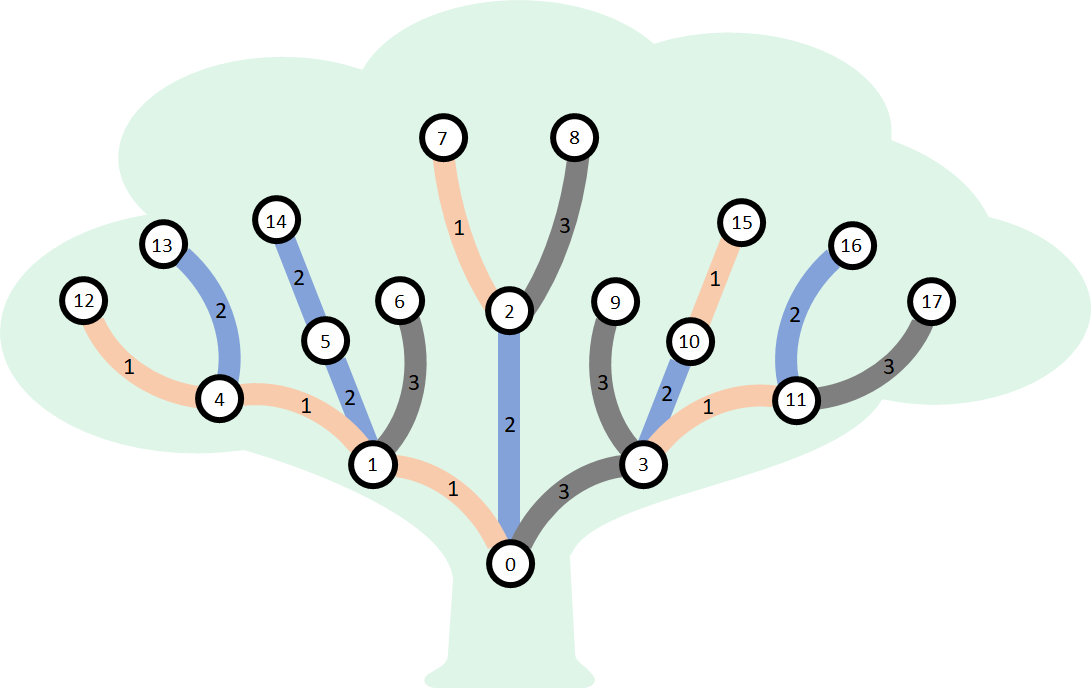
Árpád 是一位才华横溢的护林人，他喜欢研究树上被称为子树的部分。 对所有满足 $0 \le r \lt N$ 的 $r$，结点 $r$ 的子树是一个满足以下性质的结点集合 $T(r)$：
- 结点 $r$ 属于 $T(r)$。
- 如果某个结点 $x$ 属于 $T(r)$，则 $x$ 的所有子结点都属于$T(r)$。
- 除了上述情况以外，其他结点都不属于 $T(r)$。
集合 $T(r)$ 的大小记作 $|T(r)|$。
Árpád 最近发现了一个复杂但有趣的子树性质。Árpád 的发现需要用到大量的纸和笔做演算，他认为你需要做同样的事情才能完成理解。他还会给你几个例子，让你能够对它们做详细的分析。
假设我们有某个给定的 $r$，以及子树 $T(r)$ 中结点的某个置换 $v_0, v_1, \ldots, v_{|T(r)|-1}$。
对于所有满足 $1 \le i \lt |T(r)|$ 的 $i$，令 $f(i)$ 为颜色 $C[v_i]$ 在长为 $i-1$ 的颜色序列 $C[v_1], C[v_2], \ldots, C[v_{i-1}]$ 中的出现次数。
（注意，$f(1)$ 必定为 $0$，原因是其定义中要考察的颜色序列是空的。）
置换 $v_0, v_1, \ldots, v_{|T(r)|-1}$ 被称为是一个绝妙置换，当且仅当以下性质成立：
- $v_0 = r$。
- 对于所有满足 $1 \le i \lt |T(r)|$ 的 $i$，结点 $v_i$ 的父结点是 $v_{f(i)}$。
对于所有满足 $0 \le r \lt N$ 的 $r$，子树 $T(r)$ 是一棵绝妙子树，当且仅当 $T(r)$ 中结点存在某个绝妙置换。注意，根据定义，仅包含单独一个结点的子树都是绝妙的。
考虑上面给出的树的例子。可以看到，子树 $T(0)$ 和 $T(3)$ 不是绝妙的。子树 $T(14)$ 是绝妙的，因为它仅包含一个结点。接下来，我们将要说明子树 $T(1)$ 也是绝妙的。
考虑一个由不同整数构成的序列 $[v_0, v_1, v_2, v_3, v_4, v_5, v_6] = [1, 4, 5, 12, 13, 6, 14]$。这个序列是 $T(1)$ 中结点的一个置换。下图给出了这个置换。序列中每个结点旁边的数字，是该结点在置换中的索引。
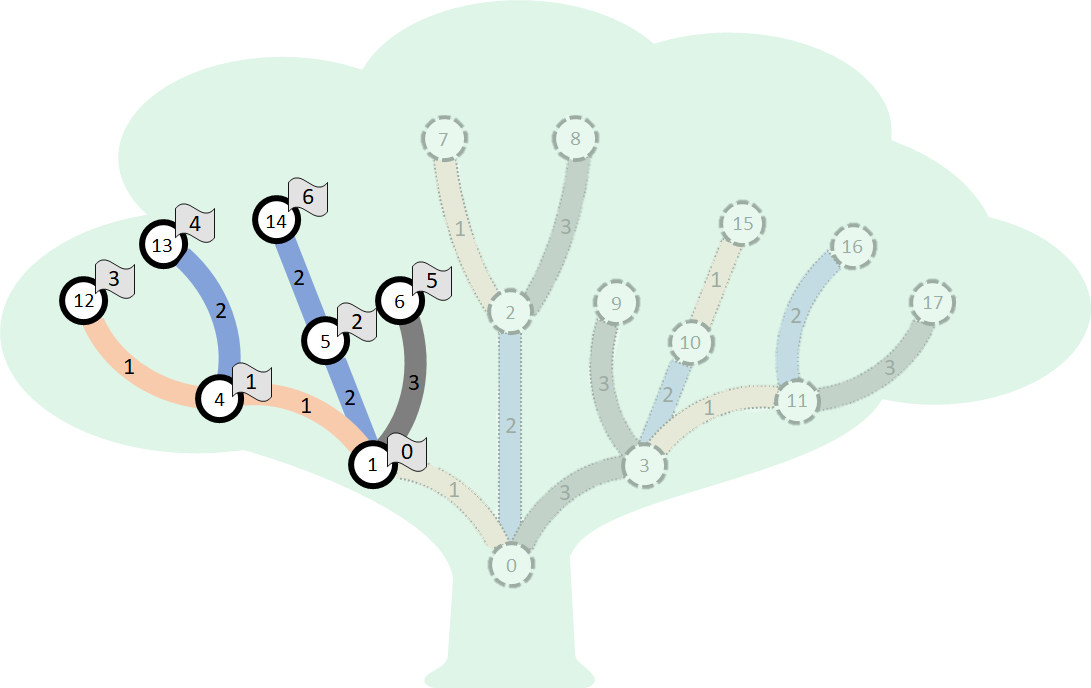
我们将要验证，这是一个绝妙置换。
- $v_0 = 1$。
- $f(1) = 0$，原因是 $C[v_1] = C[4] = 1$ 在序列 $[\,]$ 中出现了 $0$ 次。
- 相应地，$v_1$ 的父结点是 $v_0$。也就是说，$4$ 的父结点是 $1$。（形式化地，$P[4] = 1$。）
- $f(2) = 0$，原因是 $C[v_2] = C[5] = 2$ 在序列 $[1]$ 中出现了 $0$ 次。
- 相应地，$v_2$ 的父结点是 $v_0$。也就是说，$5$ 的父结点是 $1$。
- $f(3) = 1$，原因是 $C[v_3] = C[12] = 1$ 在序列 $[1, 2]$ 中出现了 $1$ 次。
- 相应地，$v_3$ 的父结点是 $v_1$。也就是说，$12$ 的父结点是 $4$。
- $f(4) = 1$，原因是 $C[v_4] = C[13] = 2$ 在序列 $[1, 2, 1]$ 中出现了 $1$ 次。
- 相应地，$v_4$ 的父结点是 $v_1$。也就是说，$13$ 的父结点是 4。
- $f(5) = 0$，原因是 $C[v_5] = C[6] = 3$ 在序列 $[1, 2, 1, 2]$ 中出现了 $0$ 次。
- 相应地，$v_5$ 的父结点是 $v_0$。也就是说，$6$ 的父结点是 $1$。
- $f(6) = 2$，原因是 $C[v_6] = C[14] = 2$ 在序列 $[1, 2, 1, 2, 3]$ 中出现了 $2$ 次。
- 相应地，$v_6$ 的父结点是 $v_2$。也就是说，$14$ 的父结点是 $5$。
由于我们能为 $T(1)$ 中的结点找到一个绝妙置换，子树 $T(1)$ 因此是一棵绝妙子树。
你的任务是，帮助 Árpád 确定 Ős Vezér 的每棵子树是否是绝妙的。
实现细节
你需要实现以下函数。
int[] beechtree(int N, int M, int[] P, int[] C)
- $N$：树中的结点数量。
- $M$：树中边的可能颜色的数量。
- $P$，$C$：长度为 $N$ 的两个数组，以描述树中的边。
- 该函数应当返回长度为 $N$ 的某个数组 $b$。 对所有满足 $0 \le r \lt N$ 的 $r$，如果 $T(r)$ 是绝妙的，则 $b[r]$ 应为 $1$，否则应为 $0$。
- 该函数在每个测试用例上恰好被调用一次。
样例
样例 1
考虑如下调用：
beechtree(4, 2, [-1, 0, 0, 0], [0, 1, 1, 2])
这棵树如下图所示：
$T(1)$，$T(2)$ 和 $T(3)$ 均各自包含单独一个结点，因此都是绝妙的。 $T(0)$ 不是绝妙的。 因此，函数应当返回 $[0, 1, 1, 1]$。
样例 2
考虑如下调用：
beechtree(18, 3,
[-1, 0, 0, 0, 1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 5, 10, 11, 11],
[0, 1, 2, 3, 1, 2, 3, 1, 3, 3, 2, 1, 1, 2, 2, 1, 2, 3])这个例子在题面中已经给出。
函数应当返回 $[0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]$。
样例 3
考虑如下调用：
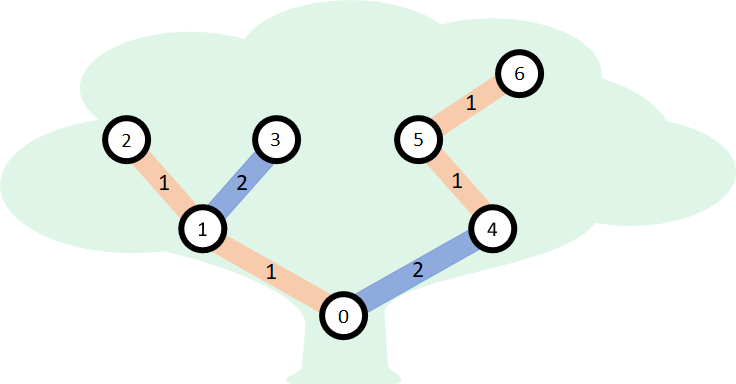
beechtree(7, 2, [-1, 0, 1, 1, 0, 4, 5], [0, 1, 1, 2, 2, 1, 1])
该例子如下图所示。
$T(0)$ 是唯一不是绝妙的子树。函数应当返回 $[0, 1, 1, 1, 1, 1, 1]$。
约束条件
- $3 \le N \le 200\,000$
- $2 \le M \le 200\,000$
- $0 \le P[i] \lt i$（对于所有满足 $1 \le i \lt N$ 的 $i$）
- $1 \le C[i] \le M$（对于所有满足 $1 \le i \lt N$ 的 $i$）
- $P[0] = -1$ 且 $C[0] = 0$
子任务
- （9 分）$N \le 8$ 且 $M \le 500$
- （5 分）边 $i$ 从结点 $i$ 连接到结点 $i-1$。也就是说，对所有满足 $1 \le i \lt N$ 的 $i$，都有 $P[i] = i-1$。
- （9 分）除了结点 $0$ 以外，其他结点要么连接到结点 $0$，要么连接到某个连接到结点 $0$ 的结点。 也就是说，对于所有满足 $1 \le i \lt N$ 的 $i$，要么有 $P[i]=0$，要么有 $P[P[i]]=0$。
- （8 分）对于所有满足 $1 \le c \le M$ 的 $c$，至多有两条边的颜色为 $c$。
- （14 分） $N \le 200$ 且 $M \le 500$
- （14 分） $N \le 2\,000$ 且 $M = 2$
- （12 分） $N \le 2\,000$
- （17 分） $M = 2$
- （12 分） 没有额外的约束条件。
评测程序示例
评测程序示例按以下格式读取输入：
- 第 $1$ 行：$N \; M$
- 第 $2$ 行：$P[0] \; P[1] \; \ldots \; P[N-1]$
- 第 $3$ 行：$C[0] \; C[1] \; \ldots \; C[N-1]$
令 $b[0], \; b[1], \; \ldots$ 表示 beechtree 所返回的数组中的元素。评测程序示例以如下格式，在单行中输出你的答案：
* 第 $1$ 行：$b[0] \; b[1] \; \ldots$
时间限制：$\texttt{1.5s}$
空间限制：$\texttt{2048MB}$
鄂公网安备 42010202000505 号