题目描述

IOI 2023 组委会有大麻烦了！他们忘记计划即将到来的 Ópusztaszer 之旅了。然而，或许一切尚未为晚 ......

在 Ópusztaszer 有 $N$ 个地标，编号为从 $0$ 到 $N-1$。某些地标之间连有双向的道路。任意一对地标之间至多连有一条道路。组委会不知道哪些地标之间有道路相连。

如果对于每三个不同的地标，它们之间都至少连有 $\delta$ 条道路，我们就称 Ópusztaszer 的路网密度是至少为 $\delta$ 的。换言之，对所有满足 $0\le u<v<w<N$ 的地标三元组 $(u,v,w)$，配对 $(u,v)$，$(v,w)$ 和 $(u,w)$ 中至少有 $\delta$ 个配对中的地标有道路相连。

组委会已知有某个正整数 $D$，满足路网密度至少为 $D$。注意， $D$ 的值不会大于 $3$。

组委会可以询问 Ópusztaszer 的电话接线员，以获取关于某些地标之间的道路连接信息。在每次询问时，必须给出两个非空的地标数组 $[A[0],\dots ,A[P-1]]$ 和 $[B[0],\dots ,B[R-1]]$。地标之间必须是两两不同的，即，

• 对于满足 $0\le i<j<P$ 的所有 $i$ 和 $j$，有 $A[i]\ne A[j]$；
• 对于满足 $0\le i<j<R$ 的所有 $i$ 和 $j$，有 $B[i]\ne B[j]$；
• 对于满足 $0\le i<P$ 且 $0\le j<R$ 的所有 $i$ 和 $j$，有 $A[i]\ne B[j]$。

对每次询问，接线员都会报告是否存在 $A$ 中的某个地标和 $B$ 中的某个地标有道路相连。更准确地说，接线员会对满足 $0\le i<P$ 和 $0\le j<R$ 的所有配对 $i$ 和 $j$ 进行尝试。如果其中某对地标 $A[i]$ 与 $B[j]$ 之间连有道路，接线员将报告 true。否则，接线员将报告 false。

一条长度为 $l$ 的路程，被定义为由不同地标 $t[0],t[1],\dots ,t[l-1]$ 构成的序列，其中对从 $0$ 到 $l-2$（包括 $0$ 和 $l-2$）的所有 $i$，地标 $t[i]$ 和 $t[i+1]$ 之间都有道路相连。如果不存在长度至少为 $l+1$ 的路程，则长度为 $l$ 的某条路程被称为是最长路程。

你的任务是通过询问接线员，帮助组委会在 Ópusztaszer 找一条最长路程。

实现细节

你需要引用头文件 longesttrip.h。

你需要实现如下函数：

int[] longest_trip(int N, int D)

• $N$：Ópusztaszer 的地标数量。
• $D$：可以保证的路网密度最小值。
• 该函数需要返回一个表示某条最长路程的数组 $t=[t[0],t[1],\dots ,t[l-1]]$。
• 对于每个测试用例，该函数都可能会被调用 多次。

上述函数可以调用如下函数：

bool are_connected(int[] A, int[] B)

• $A$：一个非空、且元素两两不同的地标数组。
• $B$：一个非空、且元素两两不同的地标数组。
• $A$ 和 $B$ 之间应无交集。
• 如果存在连接 $A$ 中某个地标以及 $B$ 中某个地标的道路，该函数返回 true。否则该函数返回 false。
• 在每次 longest_trip 调用中，该函数可以被至多调用 $32640$ 次。该函数的累计调用总数至多为 $150000$ 次。
• 对历次调用该函数时传递的数组 $A$ 和 $B$ 长度进行累计，两个数组累计长度加起来不能超过 $1500000$。

评测程序是非适应性的。每次提交都将在同一组测试用例上进行评测。换言之，在每个测试用例中，$N$ 和 $D$ 的值，以及道路所连接的地标配对，对于每次 longest_trip 调用都保持不变。

例子

样例一

考虑某个 $N=5$, $D=1$ 的场景，其中道路连接情形如下图所示：

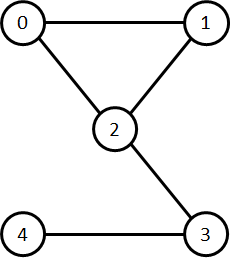
函数 longest_trip 被调用如下：

longest_trip(5, 1)

该函数可以调用 are_connected 如下。

在第四次调用后，可知 $(1,4)$，$(0,4)$，$(1,3)$ 和 $(0,3)$ 中没有哪个配对中的地标之间连有道路。由于路网的密度至少是 $D=1$，我们由三元组 $(0,3,4)$ 可知，配对 $(3,4)$ 的地标之间必须连有道路。与此相似，地标 $0$ 和 $1$ 之间必须是相连的。

至此，可以总结出 $t=[1,0,2,3,4]$ 是一条长度为 $5$ 的路程，而且不存在长度超过 $5$ 的路程。因此，函数 longest_trip 可以返回 $[1,0,2,3,4]$。

考虑另一个场景， 其中 $N=4$, $D=1$，且地标之间的道路如下图所示：

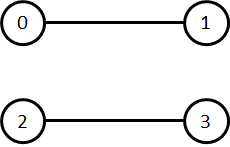
函数 longest_trip 被调用如下：

longest_trip(4, 1)

在这个场景中，最长路程的长度为 $2$。因此，在对函数 are_connected 进行少量调用后，函数 longest_trip 可以返回 $[0,1]$, $[1,0]$, $[2,3]$ 和 $[3,2]$ 中的任意一个.

样例 2

子任务 0 包含另一个测试用例用作示例，其中有 $N=256$ 个地标。

数据范围

• $3\le N\le 256$
• 对于每个测试用例，函数 longest_trip 的所有调用中 $N$ 的累计总和不超过 $1024$。
• $1\le D\le 3$

子任务

1. （5 分）$D=3$
2. （10 分）$D=2$
3. （25 分）$D=1$。令 $l^{\star }$ 表示最长路程的长度。函数 longest_trip 不必返回长度为 $l^{\star }$ 的某条路程，而应返回长度至少为 $\lceil \frac{l^{\star }}{2}\rceil$ 的某条路程。
4. （60 分）$D=1$

在子任务 4 中，你的得分将根据 longest_trip 的单次调用中对函数 are_connected 的调用数量而定。对该子任务的所有测试用例调用 longest_trip，令 $q$ 为各次调用产生的函数 are_connected 调用次数的最大值。 你在该子任务上的得分将按照下表进行计算：

如果在某个测试用例上，对函数 are_connected 的调用没有遵守实现细节部分给出的限制条件，或者 longest_trip 返回的数组是错误的，你的解答在该子任务上的得分将为 $0$。

评测程序示例

令 $C$ 为场景数量，即调用 longest_trip 的次数。 评测程序示例读取如下格式的输入数据：

• 第 $1$ 行：$C$

接下来是这 $C$ 个场景的描述数据。

评测程序示例读取每个场景如下格式的描述数据：

• 第 $1$ 行：$ND$
• 第 $1+i$ 行（$1\le i<N$）：$U_i[0]U_i[1]\dots U_i[i-1]$

这里每个 $U_i$（$1\le i<N$）均为长度为 $i$ 的数组，以给出那些有道路相连的地标配对。对于满足 $1\le i<N$ 且 $0\le j<i$ 的所有 $i$ 和 $j$：

• 如果地标 $j$ 和 $i$ 之间有道路相连，则 $U_i[j]$ 的值应为 $1$；
• 如果地标 $j$ 和 $i$ 之间没有道路相连，则 $U_i[j]$ 的值应为 $0$。

在每个场景中，在调用 longest_trip 之前，评测程序示例检查路网的密度是否至少为 $D$。如果不满足该条件，评测程序示例将输出信息 Insufficient Density 并中止。

如果检查出违反规则的行为，评测程序示例的输出为 Protocol Violation: <MSG>，这里 <MSG> 为如下错误信息之一：

• invalid array：在 are_connected 的某次调用中，数组 $A$ 和 $B$ 中至少其一
  • 为空，或
  • 有元素不是 $0$ 到 $N-1$ 之间（包含 $0$ 和 $N-1$）的整数，或
  • 有重复元素。
• non-disjoint arrays：在 are_connected 的某次调用中，数组 $A$ 和 $B$ 的交集不空。
• too many calls：函数 are_connected 在 longest trip 的当前调用中的被调用次数超过了 $32640$，或者其累计调用次数超过了 $150000$。
• too many elements：在 are_connected 的全部调用中，所传递的地标的累计数量超过了 $1500000$。

否则，令 longest_trip 函数在某个场景中的返回数组为 $t[0],t[1],\dots ,t[l-1]$，这里 $l$ 为某个非负整数。评测程序示例将对该场景按照如下格式输出三行：

• 第 $1$ 行：$l$
• 第 $2$ 行：$t[0]t[1]\dots t[l-1]$
• 第 $3$ 行：在该场景中调用 are_connected 的次数

最后，评测程序示例输出：

• 第 $1+3\cdot C$ 行：在 longest_trip 的所有调用中，函数 are_connected 被调用的最多次数

关于 Hack 格式

请在第一行数据组数前加上数据类型 D3/D2/D1Half/D1。

时间限制：$\mathtt{\text{1s}}$

空间限制：$\mathtt{\text{2048MB}}$