有一个 $n$ 列 $m$ 行的棋盘，共 $n \times m$ 个方格，我们约定行、列均从 $1$ 开始标号，且第 $i$ 列、第 $j$ 行的方格坐标记为 $(i, j)$。初始时，所有方格的颜色均为白色。现在，你要对这个棋盘进行 $q$ 次染色操作。

染色操作分为三种，分别为：

1. 将一条横线染为黑色。具体地说，给定两个方格 $(x_1, y_1)$ 和 $(x_2, y_2)$，保证 $x_1 \le x_2$，$y_1 = y_2$，将这两个方格之间的所有方格（包括这两个方格）染为黑色。
2. 将一条竖线染为黑色。具体地说，给定两个方格 $(x_1, y_1)$ 和 $(x_2, y_2)$，保证 $x_1 = x_2$，$y_1 \le y_2$，将这两个方格之间的所有方格（包括这两个方格）染为黑色。
3. 将一条斜线染为黑色。具体地说，给定两个方格 $(x_1, y_1)$ 和 $(x_2, y_2)$，保证 $x_1 \le x_2$，$x_2 - x_1 = y_2 - y_1$，将这两个方格之间斜线上所有形如 $(x_1 + i, y_1 + i)$（$0 \le i \le x_2 - x_1$）的方格染为黑色。这种染色操作发生的次数不超过 $5$ 次。

现在你想知道，在经过 $q$ 次染色后，棋盘上有多少个黑色的方格。

输入格式

输入的第一行包含一个整数 $c$，表示测试点编号。$c = 0$ 表示该测试点为样例。

输入的第二行包含三个正整数 $n, m, q$，分别表示棋盘的列、行和染色操作的次数。

接下来 $q$ 行，每行输入五个正整数 $t, x_1, y_1, x_2, y_2$，其中 $t = 1$ 表示第一种染色操作，$t = 2$ 表示第二种染色操作，$t = 3$ 表示第三种染色操作。$x_1, y_1, x_2, y_2$ 表示染色操作的四个参数。

输出格式

输出一行包含一个整数，表示棋盘上被染为黑色的方格的数量。

样例一

input

0
5 5 3
1 1 3 5 3
2 3 1 3 5
3 1 1 5 5

output

13

explanation

在这组样例中，我们一共做了三次染色操作，如下图所示。

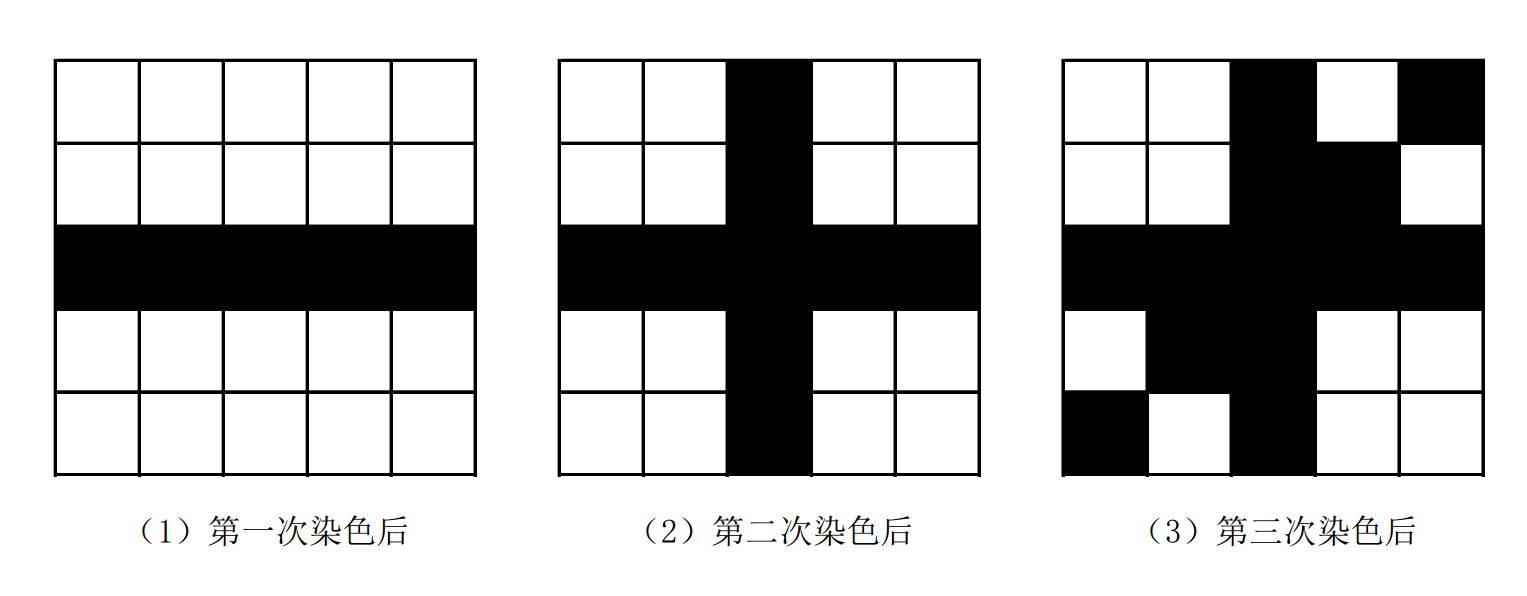
第一次操作时，将 $(1, 3), (2, 3), (3, 3), (4, 3), (5, 3)$ 染为黑色。

第二次操作时，将 $(3, 1), (3, 2), (3, 3), (3, 4), (3, 5)$ 染为黑色。

第三次操作时，将 $(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)$ 染为黑色。

样例二

见附件下载。

这个样例满足测试点 $1 \sim 5$ 的条件限制。

样例三

这个样例满足测试点 $6 \sim 9$ 的条件限制。

样例四

这个样例满足测试点 $10 \sim 13$ 的条件限制。

样例五

这个样例满足测试点 $14 \sim 17$ 的条件限制。

样例六

这个样例满足测试点 $18 \sim 19$ 的条件限制。

样例七

这个样例满足测试点 $20$ 的条件限制。

数据范围

对于所有测试数据保证：$1 \le n, m \le 10 ^ 9$，$1 \le q \le 10 ^ 5$，$1 \le x_1, x_2 \le n$，$1 \le y_1, y_2 \le m$，且最多有 $5$ 次第三种染色操作。

特殊性质 A：保证只有第一种染色操作。

特殊性质 B：保证只有第一种和第二种染色操作。

时间限制：$1\texttt{s}$

空间限制：$512\texttt{MB}$