Bu Dengklek 有一个鲶鱼塘。 这个鲶鱼塘是由 $N\times N$ 个网格单元构成的池塘。 每个单元都是相同大小的正方形。 网格各列自西向东编号为从 $0$ 到 $N-1$，各行自南向北编号为从 $0$ 到 $N-1$。 我们把坐落在网格第 $c$ 列第 $r$ 行处（$0\le c\le N-1$，$0\le r\le N-1$）的单元记为单元 $(c,r)$。

池塘里总共有 $M$ 条鲶鱼，编号为从 $0$ 到 $M-1$，分别位于不同的单元中。对每个满足 $0\le i\le M-1$ 的 $i$，鲶鱼 $i$ 在单元 $(X[i],Y[i])$ 中，其重量为 $W[i]$ 克。

Bu Dengklek 想造些长堤来抓鲶鱼。 在第 $c$ 列中长度为 $k$ 的长堤（对于所有 $0\le c\le N-1$ 和 $1\le k\le N$），是一个从第 $0$ 行跨到第 $k-1$ 行的矩形，盖住单元 $(c,0),(c,1),\dots ,(c,k-1)$。对于每一列，Bu Dengklek 可以按照她自己选择的某个长度造长堤，也可以不造。

鲶鱼 $i$ （对所有满足 $0\le i\le M-1$ 的 $i$）能被抓住，如果有某个长堤紧邻它的西侧或东侧，而且没有长堤盖住它所在的单元；也就是说，如果

• 单元 $(X[i]-1,Y[i])$ 或 $(X[i]+1,Y[i])$ 中 至少有一个 被某个长堤盖住，而且
• 没有长堤盖住单元 $(X[i],Y[i])$。

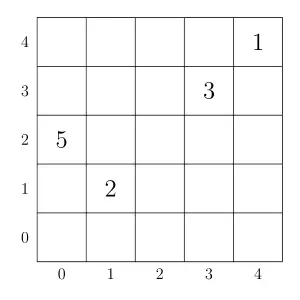
例如，考虑尺寸为 $N=5$，有 $M=4$ 条鲶鱼的池塘：

• 鲶鱼 $0$ 在单元 $(0,2)$ 中，重量为 $5$ 克。
• 鲶鱼 $1$ 在单元 $(1,1)$ 中，重量为 $2$ 克。
• 鲶鱼 $2$ 在单元 $(4,4)$ 中，重量为 $1$ 克。
• 鲶鱼 $3$ 在单元 $(3,3)$ 中，重量为 $3$ 克。

Bu Dengklek 可以这样来造长堤：

造长堤前	造长堤后

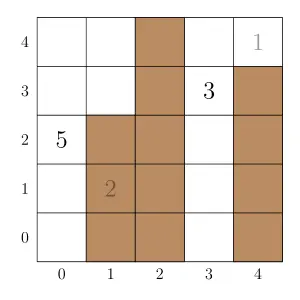单元中的数字表示该单元中鲶鱼的重量。 阴影单元被长堤盖住。 在该场景中，鲶鱼 $0$（在单元 $(0,2)$ 中）和鲶鱼 $3$（在单元 $(3,3)$ 中）能被抓住。 鲶鱼 $1$（在单元 $(1,1)$ 中）没被抓住，因为有一个长堤盖住了它所在的单元；鲶鱼 $2$（在单元 $(4,4)$ 中）没被抓住，因为没有长堤紧邻它的西侧或东侧。

Bu Dengklek 希望造出来的长堤能让被抓住的鲶鱼的总重量尽量大。 你的任务是求出 Bu Dengklek 通过造长堤能抓住的鲶鱼的最大总重量。

实现细节

你需要实现下面的函数：

int64 max_weights(int N, int M, int[] X, int[] Y, int[] W)

• $N$：池塘的尺寸。
• $M$：鲶鱼的数量。
• $X$, $Y$：长度为 $M$ 的两个数组，给出鲶鱼的位置。
• $W$：长度为 $M$ 的数组，给出鲶鱼的重量。
• 该函数需要返回一个整数，表示 Bu Dengklek 通过造长堤能抓住的鲶鱼的最大总重量。
• 该函数将被恰好调用一次。

例子

考虑如下调用：

max_weights(5, 4, [0, 1, 4, 3], [2, 1, 4, 3], [5, 2, 1, 3])

该例子的解释请见前面的题面。

在造完所述的长堤后，Bu Dengklek 能抓住鲶鱼 $0$ 和 $3$，其总重量为 $5+3=8$ 克。 因为无法造出能够抓住总重量超过 $8$ 克的鲶鱼的长堤，函数应当返回 $8$。

约束条件

• $2\le N\le 100000$
• $1\le M\le 300000$
• $0\le X[i]\le N-1$，$0\le Y[i]\le N-1$（对所有满足 $0\le i\le M-1$ 的 $i$）
• $1\le W[i]\le {10}^9$（对所有满足 $0\le i\le M-1$ 的 $i$）
• 任意两条鲶鱼都不会在同一单元中。 换句话说，$X[i]\ne X[j]$ 或 $Y[i]\ne Y[j]$（对于所有满足 $0\le i<j\le M-1$ 的 $i$ 和 $j$）。

子任务

1. （3 分） $X[i]$ 是偶数（对于所有满足 $0\le i\le M-1$ 的 $i$）
2. （6 分） $X[i]\le 1$（对于所有满足 $0\le i\le M-1$ 的 $i$）
3. （9 分） $Y[i]=0$（对于所有满足 $0\le i\le M-1$ 的 $i$）
4. （14 分） $N\le 300$，$Y[i]\le 8$（对于所有满足 $0\le i\le M-1$ 的 $i$）
5. （21 分） $N\le 300$
6. （17 分） $N\le 3000$
7. （14 分） 在每列中至多有 $2$ 条鲶鱼。
8. （16 分） 没有额外限制。

评测程序示例

评测程序示例读取如下格式的输入：

• 第 $1$ 行：$NM$
• 第 $2+i$ 行（$0\le i\le M-1$）：$X[i]Y[i]W[i]$

评测程序示例将按照如下格式打印你的答案：

• 第 $1$ 行：max_weights 的返回值

时间限制：$1\mathtt{\text{s}}$

空间限制：$1\mathtt{\text{GB}}$