这是一道交互题，本题仅支持 C++。

法老们发现了标号从 $0$ 到 $n-1$ 的 $n$ 个星球，并且在它们之间建立了一个单向传输系统。在这个传输系统中，每个传送器连接一个起始星球和一个目的星球。当游客从一个起始星球使用传送器，就可以到达对应的目的星球。需要注意的是，起始星球和目的星球有可能是同一个星球。我们使用 $(u,v)$ 表示一个起始于星球 $u$ 到达星球 $v$ 的传送器。

为了促进传输系统的广泛使用，法老们设计了一个供游客们在乘坐传送系统时可以进行的游戏。一名游客可以从任一星球出发。标号 $0,1,\dots ,k-1$（$k\le n$）的星球被称为特殊星球。当游客每次进入一个特殊星球，就可以获得一枚邮票。

目前，对于每个星球 $i$（$0\le i\le k-2)$），都建立了一个传送器 $(i,i+1)$。这 $k-1$ 个传送器叫做起始传送器。

传送器随着时间不断建立。随着传送器的建立，一名游客也许有可能获得无穷多枚邮票。准确来说，这种情况会在存在一个满足如下条件的星球序列 $w[0],w[1],\dots ,w[t]$ 时发生：

• $1\le t$。
• $0\le w[0]\le k-1$。
• $w[t]=w[0]$。
• 对于每个星球 $i$（$0\le i\le t-1$），存在一个传送器 $(w[i],w[i+1])$。

注意一名游客能够使用起始传送器和任何一个目前已经建立的传送器。

你的任务是，帮助法老验证在每次加入新的传送器后，一位游客是否能够拿到无穷多枚邮票。

实现细节

你需要实现下述函数：

init(int n, int k)

• $n$：星球数量。
• $k$：特殊星球数量。
• 这个函数只会被调用一次，早于任何一次 add_teleporter 调用。

int add_teleporter(int u, int v)

• $u$ 和 $v$：被加入传送器的起始和目的星球。
• 这个函数至多被调用 $m$ 次（$m$ 的取值范围参阅“约束条件”部分的内容）。
• 如果当传送器 $(u,v)$ 被加入后游客能够获得无穷多枚邮票，函数需要返回 $1$。否则，这个函数应该返回 $0$。
• 一旦函数返回了 $1$，你的程序将会被终止。

输入格式

评测程序示例按照如下的格式读取输入数据：

• 第 $1$ 行：$nmk$。
• 第 $2+i$ 行（$0\le i\le m-1$）：$u[i]v[i]$。

评测程序示例首先调用 init，然后按照 $i=0,1,\dots ,m-1$ 的顺序调用 add_teleporter：$u=u[i]$ 和 $v=v[i]$。

输出格式

程序将输出多次调用 add_teleporter 中首次返回 $1$ 的调用索引（$0$ 到 $m-1$，包含 $0$ 和 $m-1$）；当所有 add_teleporter 调用中都返回 $0$ 时，你的程序将输出 $m$。

如果某次 add_teleporter 调用返回了 $0$ 和 $1$ 之外的整数，评测程序示例会输出 $-1$，你的程序会被马上终止。

样例 1

input

6 5 3
3 4
5 0
4 5
5 3
1 4

output

4

explanation

考虑下面的函数调用：

init(6, 3)

在这个例子里，有 $6$ 个星球和 $3$ 个特殊星球，标号为 $0,1,2$ 的星球是特殊星球。起始传送器是 $(0,1)$ 和 $(1,2)$。

假设评测程序执行下述调用：

• (0) add_teleporter(3, 4)：应该返回 $0$。
• (1) add_teleporter(5, 0)：应该返回 $0$。
• (2) add_teleporter(4, 5)：应该返回 $0$。
• (3) add_teleporter(5, 3)：应该返回 $0$。
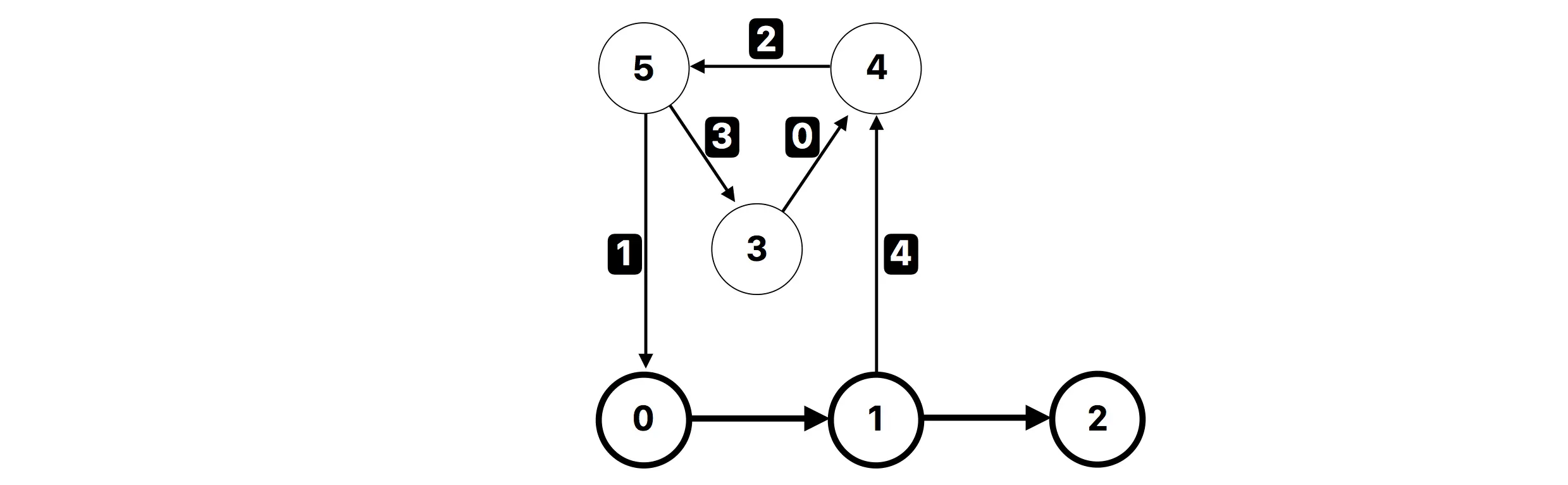
• (4) add_teleporter(1, 4)：在这种情况下，是可能获得无穷多枚邮票的。例如，游客可以从星球 $0$ 出发，按照 $1,4,5,0,1,4,5,0,\dots$ 这个顺序进行。因此，函数需要返回 $1$，进一步你的程序会被终止。

下图对于这个例子进行了说明。特殊星球和起始传送器都使用粗体字表示。通过 add_teleporter 加入的传送器，按照顺序被标记为 $0$ 到 $4$。

样例 2

input

4 1 2
1 1

output

0

explanation

考虑下面的函数调用：

init(4, 2)

在这个例子里，有 $4$ 个星球和 $2$ 个特殊星球。标号为 $0$ 和 $1$ 星球是特殊星球。起始传送器是 $(0,1)$。

假设评测程序执行下述调用：

• add_teleporter(1, 1)：当加入传送器 $(1,1)$ 后，我们就能够获得无穷多枚邮票。例如，游客从星球 $1$ 出发，可以使用传送器 $(1,1)$ 到达星球 $1$ 无限次。因此，函数需要返回 $1$，然后你的程序被终止。

样例 3

input

4 3 2
1 3
2 0
3 2

output

2

约束条件

• $1\le n\le 3\times {10}^5$。
• $1\le m\le 5\times {10}^5$。
• $1\le k\le n$。

对于每次调用 add_teleporter 函数：

• $0\le u\le n-1$ 和 $0\le v\le n-1$。
• 在传送器 $(u,v)$ 加入之前，不会有从星球 $u$ 到星球 $v$ 的传送器。

子任务

1. （$2$ 分）$n=k,n\le 100,m\le 300$。
2. （$10$ 分）$n\le 100,m\le 300$。
3. （$18$ 分）$n\le {10}^3,m\le 5\times {10}^3$。
4. （$30$ 分）$n\le 3\times {10}^4,m\le 5\times {10}^4,k\le {10}^3$。
5. （$40$ 分）没有额外的约束条件。

时间限制：$\cancel{2\mathtt{\text{s}}}4\mathtt{\text{s}}$

空间限制：$256\mathtt{\text{MB}}$