九条可怜是一个喜欢计算几何的女孩子,她画了一个特别的平面坐标系,其中
从中,她取出所有横纵坐标不全为偶数,且满足
可怜想将其中一些点染色,但相邻的点不能同时染色。具体地,对于点
可怜想知道在这个规则下最多能将多少点染色,以及染最多点的染色方案数。由于后者值可能很大,对于染色方案数,你只需要输出对
输入格式
第一行一个整数
接下来
输出格式
输出共
样例一
input
6 2 1 2 1 1 137 3 94 95 3 1998 1996 998244 353999 999999 50 120 150
output
7 4 4 1 1124 31585548 23951 33873190 1289433675488 748596399 23600 480090154
explanation
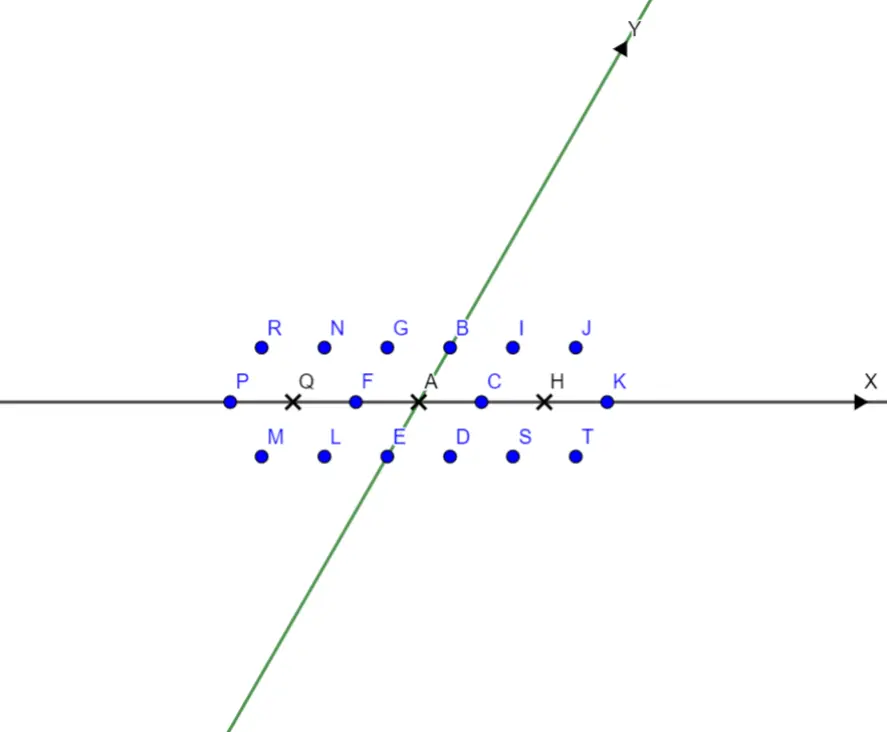
如下图所示,点
在样例的第一组数据中,满足条件的整点有
最多能染
在样例的第二组数据中,满足条件的整点有
最多能染
限制与约定
对于所有测试点:
每个测试点的具体限制见下表:
| 测试点编号 | 特殊限制 | ||
|---|---|---|---|
| 无 | |||
| 无 | |||
| 无 | |||
| 无 | |||
| 无 | |||
| 无 | |||
| 无 |
时间限制:
空间限制:

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号