活动快要结束了，活动的负责人伏特突然意识到他还没制作纪念品！

伏特找到了一件半成品，并决定将它加工完成。

半成品包含 $n$ 个具有磁力小球和 $n-1$ 根具有磁力的棍子，并且第 $i$ 根磁棍两端分别吸住了 $f_i \in [1, i]$ 号磁球和 $i+1$ 号磁球。

磁球有黑白两色，$1$ 号点是白色的，并且磁棍连接的两个小球不同色。可以证明，在这样的限制下，染色是唯一的。

伏特想要制作恰好 $k$ 件纪念品，并且由于这些小球很珍贵，他不希望浪费小球。因此他将会拆除 $k-1$ 根磁棍，使得半成品分散为 $k$ 块。

纪念品需要具有一定的特征，对于分散出的一个块，它可以作为纪念品当且仅当：所有只连接着一根磁棍的磁球同色。特别的，单个磁球也可以作为纪念品。

伏特找到了你，请你帮他选择一些磁棍拆除，或者告诉他这件半成品没法被拆成恰好 $k$ 部分。

一句话题意：给定一棵树，你需要断掉 $k-1$ 条边，使得得到的每个连通块两两叶子距离均为偶数（连通块可以为单点）。

输入格式

本题多测。第一行一个整数 $T$，表示测试数据组数。

对于每组测试数据：

第一行两个整数 $n,k$，表示磁球个数和需要制作的纪念品个数。

第二行 $n-1$ 个整数，第 $i$ 个整数 $f_i$ 表示第 $i$ 根磁棍连接 $f_i$ 和 $i+1$。

输出格式

如果不存在满足条件的方案，输出 -1，否则输出一行 $k-1$ 个整数，表示需要拆除磁棍的序号。

如有多种方案，输出任意一组均可。

样例一

input

1
6 2
1 1 3 4 1

output

2

explanation

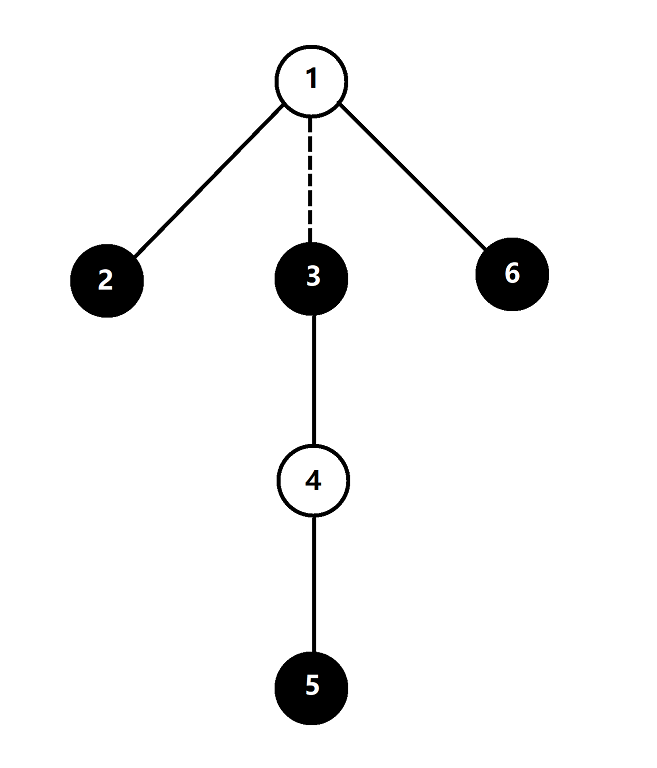
断掉 $1$ 或 $5$ 号磁棍同样是合法的方案。

样例二

input

1
3 2
1 1

output

-1

explanation

这是一条长度为 $3$ 的链，显然无法被划分成符合条件的两部分。

样例三

见附件下载中的 ex_gift3.in 和 ex_gift3.ans。

数据范围与提示

记 $S$ 为所有测试数据的 $n$ 之和。

对于所有数据，保证 $S \leq 10^6, n \geq 3, 2 \leq k \leq n, f_i \in [1, i]$。

时间限制：$\texttt{3s}$

空间限制：$\texttt{1024MB}$