【候选队互测2022】理论复杂度 - 题目

小 z 给小 m 出了一道毒瘤题。

小 m 并不会做，于是小 m 开始写暴搜。虽然小 z 曾经说过：理论复杂度和运行效率没有直接关系，但是小 m 还是想知道，暴搜的理论复杂度。她发现，她的搜索次数是在一棵树上填数的方案数。

这棵树有 $10^{10^{10}}$ 个节点，从 $1$ 开始编号。设 $r \geq 1$ 为一个参数。对于编号为 $i$ 的节点，如果 $2 \leq i \leq r + 1$ ，那么它的父亲是编号为 $i - 1$ 的节点；如果 $r + 2 \leq i$ ，它的父亲是编号为 $i - 2$ 的节点。

下图是一棵 $r = 4$ 的树，只画出了顶上的一小部分。每个圆圈为一个节点，圆圈旁边标的数为这节点的编号。

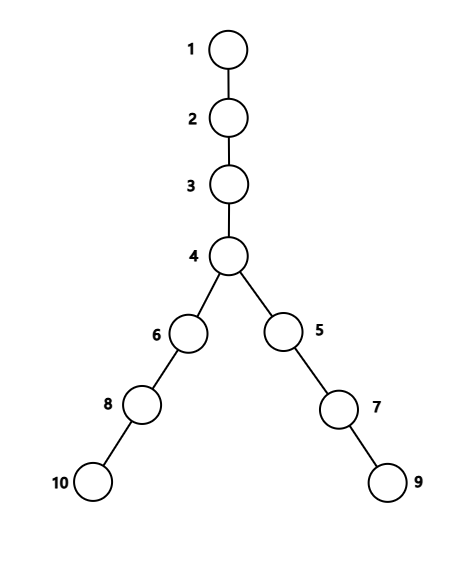
现在小 m 想给每个节点都填进一个数。填数需要满足三个条件：

填的数都是非负整数。
对于第 $i (2 \leq i)$ 个节点，它父亲填的数必须不小于它。
所填数之和恰好为 $n$ 。

小 m 想知道，对于 $n \in [1, N]$ ，有多少种方法填数。然而她也意识到了方案数非常大，因此你只需要输出答案对 $998244353$ 取模后的结果。

输入格式

一行两个整数 $N, r$ 分别表示数之和的最大值和树的形态。

输出格式

一行 $N$ 个整数，第 $i$ 个整数表示 $n = i$ 时的方案数对 $998244353$ 取模后的结果。

样例一

input

9 4

output

1 2 3 5 8 14 22 36 56

explanation

对于 $n = 5$ ，方案如下：

$[5]$
$[4, 1]$
$[3, 2]$
$[3, 1, 1]$
$[2, 2, 1]$
$[2, 1, 1, 1]$
$[1, 1, 1, 1, 1]$
$[1, 1, 1, 1, 0, 1]$

其中第 $i$ 个数表示第 $i$ 个节点填的数，未标出部分均填 $0$ 。

样例二

见附件下载。

数据范围与提示

子任务编号	$N \leq$	$r \leq$	分值
$1$	$100$	$20$	$10$
$2$	$1000$	$100$	$20$
$3$	$500000$	$1$	$10$
$4$		$2$	$30$
$5$		$500$	$30$

对于所有数据， $1 \leq N \leq 500000, 1 \leq r \leq 500$ 。

时间限制： $3s$

空间限制： $512MB$

Universal Online Judge

UOJ

#696. 【候选队互测2022】理论复杂度