这是一道交互题。

最终，UOI 主席亲自向大家宣布了大D米 AK UOI 的消息，会场响起了经久不衰的掌声与欢呼声。

然而天下没有不散的宴席，终于到了大家需要各自坐航天飞机回去的疏散日。此时，你的电话铃声响起，原来是两只外星老鼠舒克和贝塔打来的，他们的银河系航空公司在疏散日这天遭遇了难以解决的客流高峰。

银河系的星球近似地分布在了一张平面上。舒克和贝塔的航空公司控制了 $n$ 个星球的航天飞机机场，这 $n$ 个机场的位置在地图上可看做一个正 $n$ 边形的 $n$ 个顶点，按顺时针依次编号为 $1,2,\cdots ,n$。

舒克和贝塔的航空公司掌握着这 $n$ 个机场间的 $2n-3$ 条双向航线，且他们恰好构成了这个正 $n$ 边形的所有边和一个三角剖分。也即，如果把机场作为点，航线作为线画在地图上，那么我们可以看到这些航线只可能在端点处相交，且最外围的航线构成了那个正 $n$ 边形的边，而正 $n$ 边形内部被其他航线完全分成了一个个三角形。

现在由于航空需求的瞬间增长，绝大部分飞机行程已被排满，仅有两架飞机处于空闲状态。初始它们分别停在 $x$ 和 $y$ 号机场。通过往年同期 UOI 客流数据的分析，舒克和贝塔预见到，按照时间顺序接下来会依次出现 $q$ 次客流紧张事件，每次事件发生在某个特定的机场。每次事件发生后，舒克和贝塔需要选择两架空闲飞机中的恰好一架调度到对应机场增开航班缓解客流压力。保证在某个客流紧张事件结束之前，下一个客流紧张事件不会发生。某个客流紧张事件结束后对应的空闲飞机会飞回这次客流紧张事件发生的机场并恢复空闲状态。

对于每条航线，舒克和贝塔给出了一个正整数价值。为了尽可能早地到达对应机场缓解客流压力，舒克和贝塔将某架空闲飞机从机场 $a$ 调度到当前客流紧张事件发生的机场 $b$ 时，会选择从机场 $a$ 到 $b$ 的一条由若干航线（可以没有任何航线）构成的路径，满足其途径的航线的价值和是所有连接 $a,b$ 的路径中最小的。如果有多个这样的路径，他们会选择任意一条。同时为了保证航班日程表不产生过多的调整，舒克和贝塔不希望在调度飞机处理客流紧张事件以外进行额外的调度。

需要注意的是，每一次客流紧张事件发生时，舒克和贝塔可以任选两架飞机中的一架去到对应机场，而不需要比较它们需要经过的航线的价值和。特别地，即使当前客流紧张事件发生的机场停靠了一架处于空闲状态的飞机，舒克和贝塔也可以选择调度另一架飞机到当前机场。

在满足了这些条件之后，舒克和贝塔最后的想法是在这些客流紧张事件中小赚一笔。具体地，舒克和贝塔希望在依次解决 $q$ 次客流紧张事件并且航班安排满足上述要求的情况下，调度两架飞机经过的所有航线的价值和最大。一条航线经过多次，价值也计算对应多次。为了不为难你，舒克和贝塔只需要你给出这个最大值就可以了。

为了保护商业机密，舒克和贝塔并不能为你直接提供航线地图和每条航线的价值。幸运的是，他们允许你在他们的航线地图存储系统上进行至多 $L$ 次询问，每次你可以给出两个机场 $p,q$，存储系统会计算出一条连接 $p,q$ 的由若干航线构成的路径使得其是所有连接 $p,q$ 的由若干航线构成的路径（路径可以不包含任何航线）中价值和最小的，并告诉你它的价值和。

任务

本题仅支持 C++。

你必须引用 airline.h 头文件。

你需要实现下面的过程：

long long solve(int n, int x, int y, int q, std::vector<int> P, int L)

其中 $n$ 表示机场的数量，$x,y$ 表示两架空闲飞机初始所在机场，$q$ 表示客流紧张事件数量，$P$ 为一个长度为 $q$ 的数组，按照时间顺序依次描述 $q$ 次客流紧张时间发生的机场编号，$L$ 表示询问限制。你需要返回在满足题目限制的情况下，调度两架飞机经过的所有航线的最大价值和。

你可以调用以下过程和交互库进行交互：

long long distance(int p, int q)

其中 $p,q\in [1,n]$ 表示两个机场的编号。交互库会返回连接机场 $p,q$ 的所有由若干航线构成的路径中价值和最小的路径的价值和。你需要保证该函数调用次数不超过 $L$。

评测方式

样例评测库将读入如下格式的输入数据：

第一行包括五个正整数 $n,q,x,y,L$，意义如题目描述所示。

接下来 $2n-3$ 行，每行三个整数 $s,t,v$ 表示有一条连接 $s$ 与 $t$ 的价值为 $v$ 的航线。你需要保证输入的航线集合满足题目中的限制，否则不保证样例交互库可以正确完成交互过程。

接下来一行 $q$ 个用空格分隔的整数，按时间顺序依次描述每个发生客流紧张事件的机场编号。

在最终测试中，航线集合以及每条航线的价值是确定的，不会因为你的询问而改变。

样例评测库将输出如下格式的输出数据：

如果你的程序正确地完成了交互，评测库将会输出两行，第一行一个整数表示 solve 函数的返回结果，第二行一个整数表示 distance 函数调用的次数。如果你的程序没有正确完成交互，则会输出对应的交互错误信息。

在输入数据满足题目条件、询问次数不超过题目限制的情况下，保证最终评测时使用的交互库不会使用超过 $\mathtt{\text{2s}}$ 时间和 $\mathtt{\text{256MB}}$ 的内存。

样例一

input

4 4 1 3 2000000
1 2 96
2 3 27
3 4 33
4 1 96
2 4 79
2
4
4
4

output

189

explanation

该组样例的航线地图如下图所示，其中每条航线上对应的数字表示其价值。初始两架空闲飞机分别停在 $1,3$ 号机场。

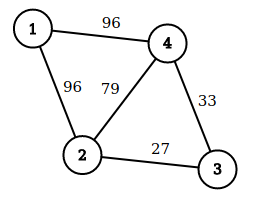
一个满足题目条件且经过的所有航线的价值和最大的方案如下：

• 第一次客流紧张事件发生在 $2$ 号机场。将停留在 $1$ 号机场的飞机调度至 $2$ 号机场，此时调度路线会是 $1\to 2$，价值和为 $96$；
• 第二次客流紧张事件发生在 $4$ 号机场。将停留在 $3$ 号机场的飞机调度至 $4$ 号机场，此时调度路线会是 $3\to 4$，价值和为 $33$；
• 第三次客流紧张事件依然发生在 $4$ 号机场。将之前停留在 $1$ 号机场、经过第一次客流紧张事件后调度到 $2$ 号机场的飞机调度至 $4$ 号机场，此时调度路线会是 $2\to 3\to 4$，价值和为 $60$；
• 第四次客流紧张事件仍然发生在 $4$ 号机场。此时两架飞机都停靠在 $4$ 号机场，调度其中任意一架都不会经过额外的航线，价值为 $0$。

对于该方案需要注意的是：

• 每一次客流紧张事件结束后，解决该次客流紧张事件的飞机会停靠在客流紧张事件发生的机场，而不是初始机场，如第一次客流紧张事件后原来停留在 $1$ 号机场的飞机停留在了 $2$ 号机场。
• 方案中将某架飞机调度到当前的客流紧张机场时一定会选择经过的航线价值和最小的路径。例如第三次客流紧张事件，将 $2$ 号机场的飞机调度到 $4$ 号机场的调度路线改为 $2\to 4$ 是不合法的。
• 方案中不能存在将某一架飞机调度到当前的非客流紧张机场的调度。
• 第三次客流紧张事件发生时，发生事件的 $4$ 号机场已经有一架空闲飞机。此时将另一架飞机调度到 $4$ 号机场是合法的；
• 同时，将一架空闲飞机调度到其所在的机场是合法的，如第四次客流紧张事件的调度。此时经过的航线价值和为 $0$；

该方案经过的航线价值和为 $96+33+60+0=189$。可以证明在题目限制下不存在更优的方案，故你实现的 solve 函数的返回值即评测库的输出应该为 $189$。

样例二

见附加文件中 ex_airline2.in 与 ex_airline2.out，该组样例满足子任务 2 的性质。

样例三

见附加文件中 ex_airline3.in 与 ex_airline3.out，该组样例满足子任务 4 的性质。

样例四

见附加文件中 ex_airline4.in 与 ex_airline4.out，该组样例满足子任务 5 的性质。

数据范围

对于 $100\mathrm{\%}$ 的数据，$3\le n\le 5\times {10}^4,1\le x,y\le n,1\le q\le 3\times {10}^4,L\in \{6\times {10}^4,2\times {10}^6\},1\le v\le {10}^9$。

温馨提示：你可以使用 $q$ 和 $L$ 的取值区分子任务。

子任务 1 和 4 的特殊性质为：

• 航线集合随机生成，生成方式为：对一个凸多边形，如果点数不超过 3 则退出；否则随机两个不相邻的顶点，在它们之间连边，并对该边分割的两个凸多边形递归处理。
• 每条航线的价值在 $[1,{10}^9]$ 内独立均匀随机。
• $q$ 次客流紧张事件发生的机场编号在 $[1,n]$ 内独立均匀随机。

子任务 5 的特殊性质为：

• $x=y=1$；
• $q$ 次客流紧张事件发生的机场编号按照时间顺序单调不降，即 solve 函数传入的 P 数组单调不降。

注意在使用 Hack 时需要保证 $L\in \{6\times {10}^4,2\times {10}^6\}$，且在 $L=6\times {10}^4$ 时需要额外满足子任务 5 的特殊性质。输入的 $q$ 可以不对应任意一个子任务。

时间限制：$\mathtt{\text{4s}}$

空间限制：$\mathtt{\text{512MB}}$