由于某些原因本题仅支持 C++, C++11 语言的提交。

在附近一个公园里，有 $n$ 座喷泉，编号为从 $0$ 到 $n - 1$。我们把喷泉看成是二维平面上的点。也就是说，喷泉 $i$（$0 \le i \le n - 1$）是一个点 $(x[i], y[i])$，这里 $x[i]$ 和 $y[i]$ 是偶数。喷泉的位置各不相同。

建筑师 Timothy 受雇来规划一些道路的建设，以及每条道路对应的长椅的摆放。每条道路都是一个长度为 $2$ 的横向或纵向的线段，其端点是两座不同的喷泉。游客应该能够沿着它们即可在任意两座喷泉之间互相抵达。在最开始时，公园里没有任何道路。

对于每条道路，都要在公园里摆放恰好一个长椅，并将其分配给（也就是面朝）这条道路。每个长椅必须摆放在某个点 $(a, b)$ 上，这里 $a$ 和 $b$ 都是奇数。所有长椅的位置必须都是不同的。在 $(a, b)$ 处的长椅，只能分配给两个端点均为 $(a - 1, b - 1)$，$(a - 1, b + 1)$，$(a + 1, b - 1)$ 和 $(a + 1, b + 1)$ 其中之一的道路。举例来说，在 $(3, 3)$ 处的长椅只能分配给下面四条线段所表示的道路之一：$(2, 2) - (2, 4)$，$(2, 4) - (4, 4)$，$(4, 4) - (4, 2)$，$(4, 2) - (2, 2)$。

请帮助 Timothy 判断一下，能否在满足上述所有要求的前提下，造出所有道路，并摆放和分配长椅。如果这能做到，请给他一个可行的解决方案。如果有多个满足所有要求的可行方案，你可以报告其中的任意方案。

实现细节

你必须引用 parks.h 头文件。

你要实现以下函数：

int construct_roads(int[] x, int[] y)

• $x, y$：长度为 $n$ 的两个数组。对所有 $i$（$0 \le i \le n - 1$），喷泉 $i$ 是一个点 $(x[i], y[i])$，这里 $x[i]$ 和 $y[i]$ 都是偶数。
• 如果存在某个建设方案，函数应当调用 build（参见下文）恰好一次来报告建设方案，并紧接着返回 $1$。
• 否则，函数应当返回 $0$，并且不做 build 的任何调用。
• 该函数将被调用恰好一次。

你实现的函数可以调用下面的函数，以提供一个可行的道路建设与长椅摆放方案：

void build(int[] u, int[] v, int[] a, int[] b)

设 $m$ 为建设方案中道路的条数。

• $u, v$：长度为 $m$ 的两个数组，表示要建造的道路。这些道路的编号为从 $0$ 到 $m - 1$。对所有的 $j$（$0 \le j \le m - 1$），道路 $j$ 要连接喷泉 $u[j]$ 和 $v[j]$。每条道路必须是长度为 $2$ 的横向或纵向线段。任意两条不同的道路，最多只能有一个公共端点（某个喷泉）。这些道路在建成之后，必须能够沿着它们就可以在任意两个喷泉之间互相抵达。
• $a, b$：长度为 $m$ 的两个数组，表示长椅。对所有的 $j$（$0 \le j \le m - 1$），将在 $(a[j], b[j])$ 处摆放一个长椅，并且分配给道路 $j$。不同的长椅不能摆放在同一位置。

输入格式

评测程序示例读取如下格式的输入：

• 第 $1$ 行：$n$
• 第 $2 + i$ 行（$0 \le i \le n - 1$）：$x[i] \; y[i]$

输出格式

评测程序示例的输出结果为如下格式：

• 第 $1$ 行：construct_roads 的返回值

如果 construct_roads 的返回值为 $1$，而且调用过 build(u, v, a, b)，评测程序示例将额外输出：

• 第 $2$ 行：$m$
• 第 $3 + j$ 行（$0 \le j \le m - 1$）：$u[j] \; v[j] \; a[j] \; b[j]$

样例一

input

5
4 4
4 6
6 4
4 2
2 4

output

1
4
0 2 5 5
0 1 3 5
3 0 5 3
4 0 3 3

explanation

考虑如下调用：

construct_roads([4, 4, 6, 4, 2], [4, 6, 4, 2, 4])

这意味着总共有 $5$ 座喷泉：

• 喷泉 $0$ 坐落在 $(4, 4)$ 处，
• 喷泉 $1$ 坐落在 $(4, 6)$ 处，
• 喷泉 $2$ 坐落在 $(6, 4)$ 处，
• 喷泉 $3$ 坐落在 $(4, 2)$ 处，
• 喷泉 $4$ 坐落在 $(2, 4)$ 处。

可以建造下面这样 $4$ 条道路，其中每条道路连接两座喷泉，并且摆放着对应的长椅：

该方案对应下图：

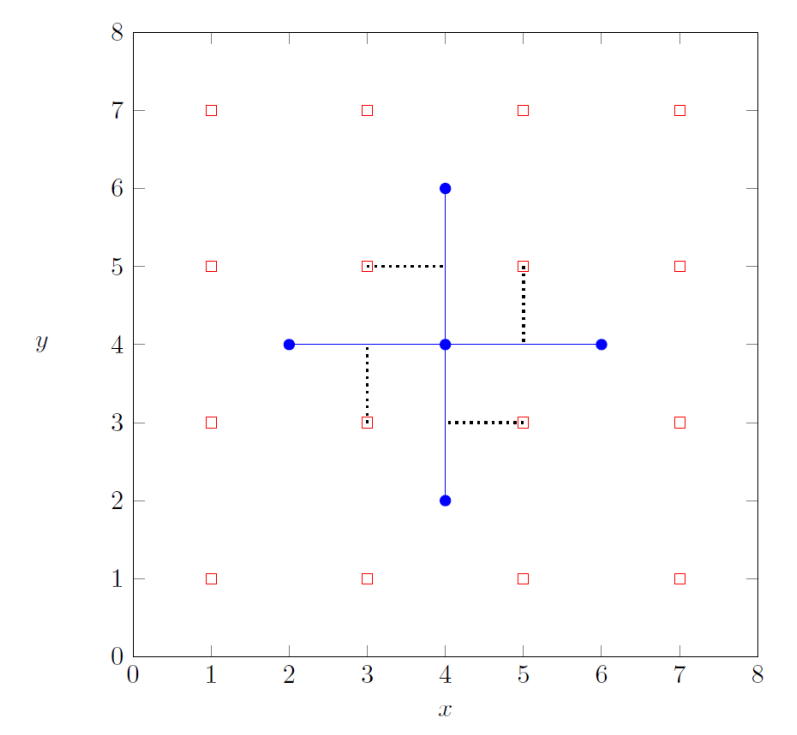
为报告此方案，construct_roads 应当做如下调用：

build([0, 0, 3, 4], [2, 1, 0, 0], [5, 3, 5, 3], [5, 5, 3, 3])

随后它应当返回 $1$。

注意，在这个例子中，有多个满足要求的方案，它们都将被视为正确。例如，调用 build([1, 2, 3, 4], [0, 0, 0, 0], [5, 5, 3, 3], [5, 3, 3, 5]) 并返回 $1$，也是正确的。

样例二

input

2
2 2
4 6

output

0

explanation

考虑如下调用：

construct_roads([2, 4], [2, 6])

喷泉 $0$ 坐落在 $(2, 2)$ 处，而喷泉 $1$ 坐落在 $(4, 6)$ 处。由于不可能建造出满足要求的道路，construct_roads 应当返回 $0$，并且不做 build 的任何调用。

数据范围

对于所有数据：

• $1 \le n \le 200 \, 000$
• $2 \le x[i], y[i] \le 200 \, 000$（对于所有 $0 \le i \le n - 1$）
• $x[i]$ 和 $y[i]$ 都是偶数（对于所有 $0 \le i \le n - 1$）
• 任意两座喷泉的位置均不相同

时间限制：$3\texttt{s}$

空间限制：$2\texttt{GB}$