在泗水市，有 $N$ 个路口（编号从 $0$ 到 $N-1$))。这些路口由 $N-1$ 条双向道路连接（编号从 $0$ 到 $N-2$)，因此通过这些道路，任意一对路口之间都有一条唯一的路径。$i$ 号道路 $(0 \le i \le N-2)$ 连接着 $U[i]$ 号和 $V[i]$ 号路口。

为了提高环保意识，泗水市长 Pak Dengklek 计划举办无车日。为了鼓励该活动，Pak Dengklek 将组织封路。Pak Dengklek 将首先选择一个非负整数 $k$，然后封闭一些道路，以使每个路口只能直接连接至多 $k$ 条未封闭的道路。封闭 $i$ 号道路的成本为 $W[i]$。

请你帮助 Pak Dengklek 对每个可能的非负整数 $k (0 \le k \le N-1)$ 计算封闭道路的最低总成本。

实现细节

你需要实现下列函数：

int64[] minimum_closure_costs(int N, int[] U, int[] V, int[] W)

• $N$：泗水市的路口数量。
• $U$ 和 $V$：大小为 $N-1$ 的数组，其中 $U[i]$ 号路口和 $V[i]$ 路口通过 $i$ 号道路直接连接。
• $W$：大小为 $N-1$ 的数组，其中封闭 $i$ 号道路的成本为 $W[i]$。
• 该函数需要返回一个大小为 $N$ 的数组。对每个 $k (0 \le k \le N-1)$，$k$ 号元素是使得每个路口与至多 $k$ 条未封闭道路直接连接的最低总成本。
• 该函数将被调用恰好一次。

例子

例子一

考虑如下调用:

minimum_closure_costs(5, [0, 0, 0, 2], [1, 2, 3, 4], [1, 4, 3, 2])

这个例子中共有 $5$ 个路口和 $4$ 条道路，分别连接着路口 $(0,1),(0,2),(0,3)$ 和 $(2,4)$，封闭它们的成本依次为 $1,4,3$ 和 $2$。

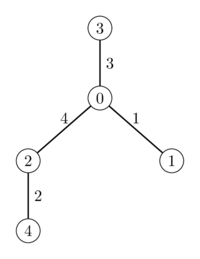
为了得到最低的总成本：

• 如果 Pak_Dengklek 选择 $k=0$，那么所有道路都需要封闭，总成本为 $1+4+3+2=10$；
• 如果 Pak_Dengklek 选择 $k=1$，那么需要封闭 $0$ 号道路和 $1$ 号道路，总成本为 $1+4=5$；
• 如果 Pak_Dengklek 选择 $k=2$，那么需要封闭 $0$ 号道路，总成本为 $1$；
• 如果 Pak_Dengklek 选择 $k=3$ 或 $k=4$，那么没有道路需要封闭。

因此，minimum_closure_costs 应该返回数组 $[10,5,1,0,0]$。

例子二

考虑如下调用：

minimum_closure_costs(4, [0, 2, 0], [1, 0, 3], [5, 10, 5])

这个例子中共有 $4$ 个路口和 $3$ 条道路，分别连接着路口 $(0,1),(2,0)$ 和 $(0,3)$，封闭它们的成本依次为 $5,10$ 和 $5$。

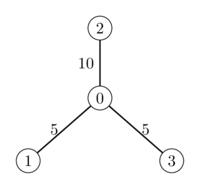
为了得到最低的总成本:

• 如果 PakDengklek 选择 $k=0$，那么所有道路都需要封闭，总成本为 $5+10+5=20$；
• 如果 PakDengklek 选择 $k=1$，那么需要封闭 $0$ 号道路和 $2$ 号道路，总成本为 $5+5=10$；
• 如果 PakDengklek 选择 $k=2$，那么需要封闭 $0$ 号道路或 $2$ 号道路，总成本为 $5$；
• 如果 PakDengklek 选择 $k=3$，那么没有道路需要封闭。

因此，minimum_closure_costs 应该返回数组 $[20,10,5,0]$。

输入格式

示例测试程序按如下格式读取输入数据:

• 第 $1$ 行：$N$
• 第 $2+i (0 \le i \le N-2)$ 行：$U[i]\ V[i]\ W[i]$

输出格式

示例测试程序输出仅一行，包含一个数组，表示 minimum_closure_costs 的返回值。

限制与约定

• $2≤N≤10^5$
• $0 \le U[i],V[i] \le N-1 (0 \le i \le N-2)$
• 任意一对路口可以通过道路互相到达。
• $1 \le W[i] \le 10^9 (0 \le i \le N-2)$。

子任务：

实际测试中，前 22 个 subtask 为数据包，后 7 个 subtask 为 7 个子任务。

1. ($5$ 分) $U[i]=0 (0 \le i \le N-2)$
2. ($7$ 分) $U[i]=i, V[i]=i+1 (0 \le i \le N-2)$
3. ($14$ 分) $N \le 200$
4. ($10$ 分) $N \le 2000$
5. ($17$ 分) $W[i]=1 (0 \le i \le N-2)$
6. ($25$ 分) $W[i] \le 10 (0 \le i \le N-2)$
7. ($22$ 分) 无附加限制

时间限制：$1\texttt{s}$

空间限制：$1\texttt{GB}$

下载

样例数据下载