JOI 王国可以用一个 $xy$-平面表示。JOI 王国中有 $N$ 座房子，从 $1$ 到 $N$ 标号。第 $i$（$1 \le i \le n$）座房子的坐标为 $(X_i, Y_i)$。不同的房子的坐标不同。每座房子中都有一位居民。居住在房子 $i$ 中的居民称作居民 $i$。

JOI 王国内的黄金周假期要开始了。在 $0$ 时刻，每位居民都会离开房子并开始他们的旅行。一开始，每位居民需要在“东”、“西”、“南”、“北”中选择一个方向开始旅行。他们遵循如下方式旅行：

• 如果居民 $i$ 选择了“东”，这位居民将会以 $1$ 的速度向着 $x$ 轴正方向移动。换句话说，在 $t$（$t \ge 0$）时刻，居民 $i$ 的坐标变为 $(X_i + t, Y_i)$。
• 如果居民 $i$ 选择了“西”，这位居民将会以 $1$ 的速度向着 $x$ 轴负方向移动。换句话说，在 $t$（$t \ge 0$）时刻，居民 $i$ 的坐标变为 $(X_i - t, Y_i)$。
• 如果居民 $i$ 选择了“南”，这位居民将会以 $1$ 的速度向着 $y$ 轴负方向移动。换句话说，在 $t$（$t \ge 0$）时刻，居民 $i$ 的坐标变为 $(X_i, Y_i - t)$。
• 如果居民 $i$ 选择了“北”，这位居民将会以 $1$ 的速度向着 $y$ 轴正方向移动。换句话说，在 $t$（$t \ge 0$）时刻，居民 $i$ 的坐标变为 $(X_i, Y_i + t)$。

不幸的是，在 $0$ 时刻，居民 $1$ 感染了 IOI 热病，这是一种最近发现的传染病。在 $0$ 时刻，除了居民 $1$ 以外没有其他感染者。IOI 热病在居民中的传播遵循如下方式：

• 假设在某一时刻，居民 $a$（$1 \le a \le N$）和居民 $b$（$1 \le b \le N$）有着相同的坐标，并且居民 $a$ 感染了 IOI 热病，而居民 $b$ 没有感染 IOI 热病，则居民 $b$ 就会感染上 IOI 热病。

IOI 热病没有其他传染方式。不仅如此，IOI 热病是一个无法治愈的疾病，被感染的居民是不会康复的。

作为 JOI 王国的首相，你需要预估当所有居民做出了最坏可能的决定时，会有多少居民感染上 IOI 热病。

给定房子的数量和每座房子的坐标，请编写一个程序，计算在 ${10}^{100}$ 时刻的可能最多感染居民数。

输入格式

第一行，一个正整数 $N$。

接下来 $N$ 行，第 $i$ 行两个整数 $X_i, Y_i$。

输出格式

输出一行，一个数，表示在 ${10}^{100}$ 时刻的可能最多感染居民数。

样例一

input

2
0 0
4 3

output

1

explanation

在此样例中，房子的位置如下：

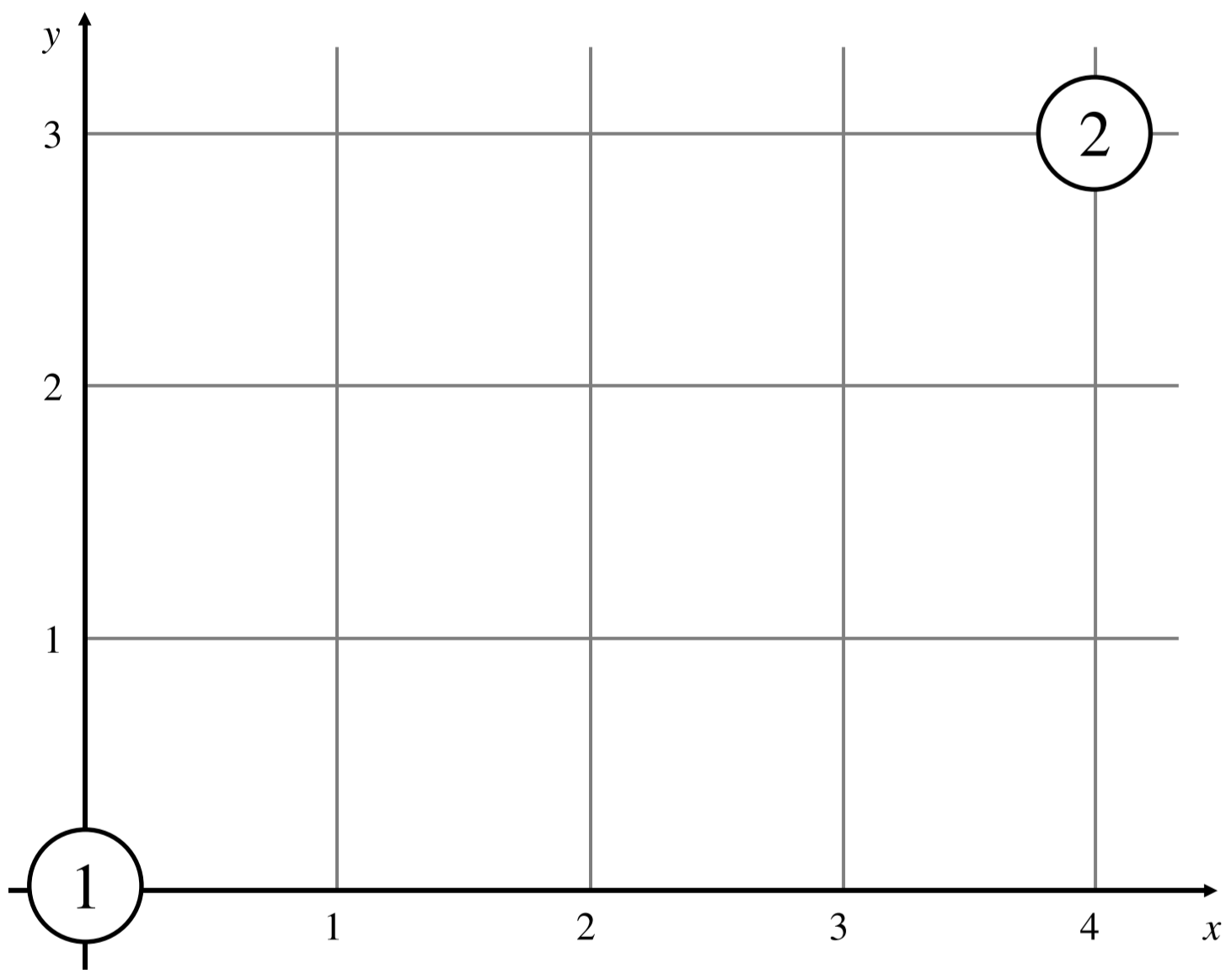
举个例子，假设居民 $1$ 选择了“东”，居民 $2$ 选择了“西”。

则在任何时刻，居民 $1$ 和 $2$ 的坐标都是不同的，于是居民 $2$ 不会被感染。所以居民 $1$ 是在 ${10}^{100}$ 时刻的唯一感染居民。感染居民数为 $1$。

无论居民 $1$ 和 $2$ 做出的选择如何，感染居民数不可能大于 $1$。所以可能最多感染居民数为 $1$，输出 $1$。

此样例满足子任务 $1, 2, 3, 4, 5, 6, 7$ 的限制。

样例二

input

3
1 2
2 1
4 3

output

3

explanation

在此样例中，房子的位置如下：

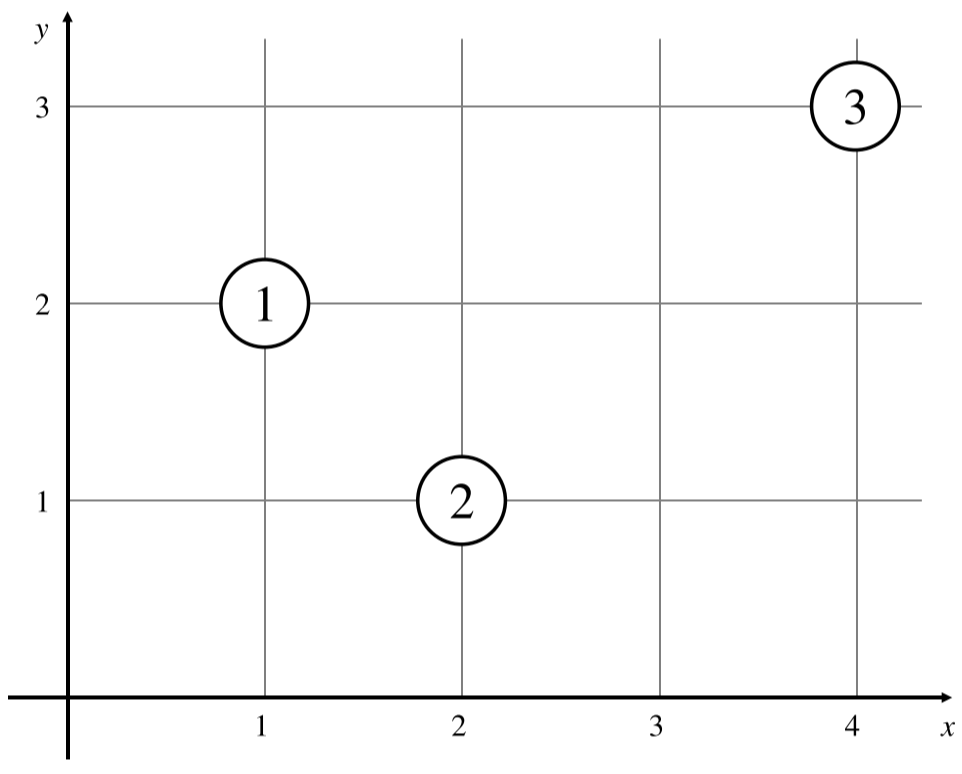
举个例子，假设居民 $1$ 选择了“东”，居民 $2$ 选择了“北”，居民 $3$ 选择了“西”。则 IOI 热病在居民中通过如下方式传染：

• 在时刻 $0$，居民 $1$ 是唯一感染者。
• 在时刻 $1$，居民 $1, 2, 3$ 的坐标分别是 $(2, 2), (2, 2), (3, 3)$。居民 $1$ 和 $2$ 的坐标相同。此时居民 $1$ 感染了 IOI 热病，而居民 $2$ 没有感染 IOI 热病。于是居民 $2$ 感染上了 IOI 热病。
• 在时刻 $2$，居民 $1, 2, 3$ 的坐标分别是 $(3, 2), (2, 3), (2, 3)$。居民 $2$ 和 $3$ 的坐标相同。此时居民 $2$ 感染了 IOI 热病，而居民 $3$ 没有感染 IOI 热病。于是居民 $3$ 感染上了 IOI 热病。

最终，感染居民数达到了 $3$。由于这是最大可能值，输出 $3$。

此样例满足子任务 $1, 2, 4, 5, 6, 7$ 的限制。

样例三

input

2
20 20
20 21

output

2

explanation

假设居民 $1$ 选择了“北”，居民 $2$ 选择了“南”。则 IOI 热病在居民中通过如下方式传染：

• 在时刻 $0$，居民 $1$ 是唯一感染者。
• 在时刻 $1$，居民 $1, 2$ 的坐标都是 $(20, 20.5)$。居民 $1$ 和 $2$ 的坐标相同。此时居民 $1$ 感染了 IOI 热病，而居民 $2$ 没有感染 IOI 热病。于是居民 $2$ 感染上了 IOI 热病。

最终，感染居民数达到了 $2$。由于这是最大可能值，输出 $2$。

此样例满足子任务 $5, 7$ 的限制。

样例四

input

15
5 6
2 9
12 0
4 11
3 12
6 5
0 8
9 10
11 13
8 7
13 2
1 1
7 14
10 4
14 3

output

9

explanation

此样例满足子任务 $2, 4, 5, 6, 7$ 的限制。

样例五

input

30
275810186 246609547
122805872 99671769
243507947 220373844
281305347 252104708
237805644 214671541
172469077 149334974
222589229 229887956
160653451 208404690
241378966 211098219
144302355 224755786
186392385 163258282
199129390 169928751
294937491 265736852
196096122 172962019
314342944 285142305
202720470 166337671
157037485 133903382
263858979 240724876
210720220 181519581
296402036 267201397
186021287 183036854
195081930 173976211
328293029 299092390
261195361 238061258
323595085 294394446
299933764 270733125
240976723 128081418
188501753 165367650
277832422 248631783
119896220 96762117

output

11

explanation

此样例满足子任务 $4, 5, 6, 7$ 的限制。

限制与约定

本题采用捆绑测试。

对于 $100 \%$ 的数据，$1 \le N \le {10}^5$，$0 \le X_i, Y_i \le 5 \times {10}^8$，$(X_i, Y_i) \ne (X_j, Y_j)$（$i < j$）。

每个子任务的具体限制见下表：

时间限制：$\texttt{5s}$

空间限制：$\texttt{512MB}$

下载

样例数据下载