如果本题评测出现问题，请联系管理员。

新加坡的互联网主干网由 $n$ 个网络站点组成，这些站点分配了从 $0$ 到 $n-1$ 的序号。互联网中还有 $n-1$ 条双向链路，它们从 $0$ 到 $n-2$ 编号。每条链路连接两个不同的站点。被一条链路连接着的两个站点互相称作对方的邻居。

一个由互不相同的站点所组成的站点序列 $a_0,a_1,\cdots ,a_p$ 被称作一条从站点 $x$ 到站点 $y$ 的路径，当且仅当 $a_0=x$，$a_p=y$，并且序列中每两个连续的站点都是邻居。保证从任意站点 $x$ 到任意其他站点 $y$ 有且仅有一条路径。

任意站点 $x$ 可以生成一个数据包，并把它发送给任意其他站点 $y$，站点 $y$ 称作这个数据包的目的站点。数据包需要按下述规则在站点 $x$ 到站点 $y$ 的唯一路径上进行路由。假设数据包当前发送到了站点 $z$，其中 $y$ 是数据包的目的站点且 $z\ne y$，则站点 $z$ 会：

1. 执行路由函数，找到 $z$ 到 $y$ 的唯一路径中 $z$ 的邻居。然后
2. 将数据包转发给这个邻居。

然而，站点有存储内存限制，可能无法存下路由函数中需要使用的完整的主干网链路列表。

你的任务是实现主干网的路由机制，它由两个函数组成：

• 第一个函数的输入参数为 $n$、主干网链路的列表和一个整数 $k\ge n-1$。该函数需要为每个站点分配一个独一无二的编号，其大小在 $0$ 到 $k$ 之间（包括 $0$ 和 $k$）。
• 第二个函数是路由函数，它在站点编号分配好后部署到所有站点上。
  • 它的输入参数如下：
    • $s$，数据包当前所处的站点的编号，
    • $t$，数据包的目的站点的编号（$t\ne s$），
    • $c$，表示 $s$ 的所有邻居站点的编号的列表。
  • 该函数应该返回一个 $s$ 的邻居的编号，表示数据包需要转发到的下个站点。

在每个子任务中，你的得分取决于所有站点被分配到的编号的最大值（通常来说，编号最大值越小越好）。

实现细节

你必须引用 stations.h 头文件。

你需要实现下列函数：

int[] label(int n, int k, int[] u, int[] v)

• $n$：主干网中站点的数量。
• $k$：可用的编号的最大值。
• $u$ 和 $v$：大小为 $n-1$ 的数组，表示链路。对每个 $i$（$0\le i\le n-2$），链路 $i$ 连接着序号为 $u[i]$ 和 $v[i]$ 的站点。
• 该函数应该返回一个大小为 $n$ 的数组 $L$。对每个 $i$（$0\le i\le n-1$），$L[i]$ 表示序号为 $i$ 的站点所分配到的编号。数组 $L$ 中的所有元素必须互不相同并且大小在 $0$ 到 $k$ 之间。

int find_next_station(int s, int t, int[] c)

• $s$：数据包当前所在站点的编号。
• $t$：数据包目的站点的编号。
• $c$：一个数组，包含 $s$ 的所有邻居的编号。数组 $c$ 按照元素大小升序排列。
• 该函数应该返回一个 $s$ 的邻居的编号，表示数据包需要转发到的下个站点。

每个测试用例包含一个或多个独立的场景（也就是不同的主干网描述）。对于一个包含 $r$ 个场景的测试用例，调用上述函数的评测程序会按下列步骤运行恰好两次。

程序第一次运行期间：

• label 函数被调用 $r$ 次，

• 返回的编号将被评测系统保存，并且

• find_next_station 不会被调用。

程序第二次运行期间：

• find_next_station 会被调用若干次。对于每次调用，评测程序会选择任意某个场景，该场景中的 label 函数所返回的编号方式将用于本次 find_next_station 调用。

• label 不会被调用。

特别地，在评测程序第一次运行期间，保存在静态或全局变量中的信息将无法在 find_next_station 函数中使用。

例子

考虑下列调用：

label(5, 10, [0, 1, 1, 2], [1, 2, 3, 4])

共有 $5$ 个站点和 $4$ 条链路，链路对应的站点序号对分别为$(0,1),(1,2),(1,3)$ 和 $(2,4)$。编号的大小范围为 $0$ 到 $k=10$。

为了返回下列编号方案：

函数 label 应该返回 $[6,2,9,3,7]$。下图中的数字表示站点的序号（左图）与分配到的编号（右图）。

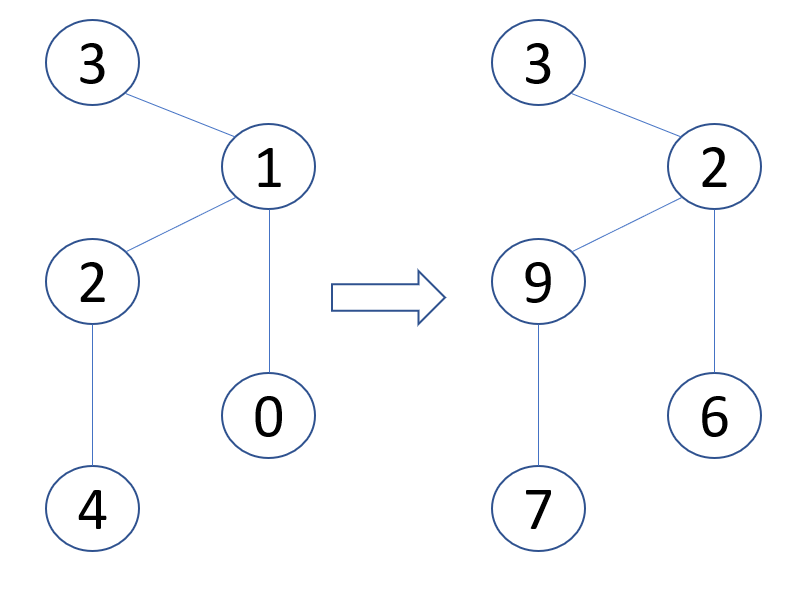
假设编号按照上图所示进行分配，考虑下列的调用：

find_next_station(9, 6, [2, 7])

它表示数据包当前所处的站点编号为 $9$，其目的站点的编号为 $6$。从当前站点到目的站点的路径上，

站点编号依次为 $[9,2,6]$。因此，函数应该返回 $2$，表示数据包应该转发给编号为 $2$ 的站点（其序号为 $1$）。

考虑另一个可能的调用：

find_next_station(2, 3, [3, 6, 9])

该函数应该返回 $3$，因为目的站点（编号 $3$）是当前站点（编号 $2$）的邻居，因此目的站点直接接收到了数据包。

约束条件

• $1\le r\le 10$

对于 label 的每次调用：

• $2\le n\le 1000$
• $k\ge n-1$
• $0\le u[i],v[i]\le n-1$ （对于所有 $0\le i\le n-2$）

对于 find_next_station 的每次调用，其输入参数来自于任意选择的某次之前对 label 的调用。

考虑它所产生的编号，

• $s$ 和 $t$ 是两个不同站点的编号。

• $c$ 是编号为 $s$ 的站点的所有邻居的编号的序列，升序排列。

对于每个测试用例，所有场景加到一起，传递给函数 find_next_station 的所有数组 $c$ 的总长度不超过 $100000$。

子任务

1. （5分）$k=1000$，不会出现拥有多于 $2$ 个邻居的站点。
2. （8分）$k=1000$，链路 $i$ 连接站点 $i+1$ 和 $\lfloor \frac{i}{2}\rfloor$。
3. （16分）$k=1000000$，最多一个站点拥有多于 $2$ 个的邻居。
4. （10分）$n\le 8,k={10}^9$
5. （61分）$k={10}^9$

在子任务 5 中，你可以获得部分分。 令 $m$ 为所有场景中 label 返回的最大编号。 对于这个子任务，你的得分将根据下表计算得到：

评测程序示例

评测程序示例以如下格式读取输入数据：

• 第 $1$ 行：$r$

接下来是 $r$ 块内容，每块描述了一个单独的场景，格式如下：

• 第 $1$ 行：$n$ $k$
• 第 $2+i$（$0\le i\le n-2$）行: $u[i]v[i]$
• 第 $1+n$ 行： $q$，find_next_station 的调用次数
• 第 $2+n+j$（$0\le j\le q-1$）行: $z[j]$ $y[j]$ $w[j]$，第 $j$ 次调用 find_next_station 时所涉及的站点的序号。此时，数据包在站点 $z[j]$，目的站点为 $y[j]$，应该要转发给站点 $w[j]$。

评测程序示例以如下格式打印你的结果：

• 第 $1$ 行：$m$

接下来是 $r$ 块内容，分别对应输入中的场景。每块的格式如下：

• 第 $1+j$（$0\le j\le q-1$）行：站点的序号，它所对应的编号是第 $j$ 次调用 find_next_station 时返回的结果。

注意：评测程序示例每次执行时会同时调用 label 和 find_next_station。

hack

在 hack 时，数据格式与上述类似，但是您需要在最后额外添加一行两个数，第一个数为 0/1，表示是否给予部分分，第二个数为 $[0,2^{31}-1]$ 内的整数，为打乱询问顺序的种子。

限制与约定

时间限制：$1\mathtt{\text{s}}$

空间限制：$1\mathtt{\text{GB}}$

下载

样例及测评库下载