由于某些原因本题仅支持 C++, C++11 语言的提交。

滨海湾花园是新加坡的一个大型自然公园。公园内有 $n$ 个塔，称之为「擎天树」。这些塔的编号为 $0$ 到 $n-1$。我们希望建立一个桥的集合（桥的数目大于等于 $0$）。每一座桥连接两个不同的塔，而且可以双向通行。没有两座桥连接相同的一对塔。

一条从塔 $x$ 到塔 $y$ 的路径是一个满足以下条件的塔序列（塔的数目大于等于 $1$）：

• 序列的第一个元素是 $x$，

• 序列的最后一个元素是 $y$，

• 序列中所有元素互不相同，

• 序列中每两个相邻元素（塔）都是被某一座桥连接起来的。

注意根据定义，一个塔到它自己有且仅有一条路径，并且从塔 $i$ 到塔 $j$ 的不同路径的数目和从塔 $j$ 到塔 $i$ 的不同路径的数目是一样的。

负责该项设计的首席设计师希望待建造的桥梁要符合：任意给定 $0\le i,j\le n-1$，恰好有 $p_{i,j}$ 条从塔 $i$ 到塔 $j$ 的不同路径，其中 $0\le p_{i,j}\le 3$。

请构造一个桥的集合来满足设计师的要求，或判定这样的桥梁集合不可能存在。

实现细节

你必须引用 supertrees.h 头文件。

你需要实现下面的这个函数：

int construct(std::vector<std::vector<int>> p)

• $p$：一个表示设计师要求的 $n\times n$ 数组。

• 如果这个建设方案是存在的，该函数应该恰好调用一次 build（见下文）来给出建设方案，然后应返回 $1$。

否则，该函数应该返回 $0$，并且不要调用 build。

该函数将被调用恰好一次。

函数 build 定义如下：

void build(std::vector<std::vector<int>> b)

• $b$：一个 $n\times n$ 的数组，$b_{i,j}=1$ 表示有一座桥连接塔 $i$ 和塔 $j$，否则 $b_{i,j}=0$。

注意该数组必须满足：对所有 $0\le i,j\le n-1$，$b_{i,j}=b_{j,i}$；并且对所有 $0\le i\le n-1$，$b_{i,i}=0$。

输入格式

评测程序示例以如下格式读取输入数据：

• 第 $1$ 行：$n$
• 第 $2+i$ 行（$0\le i\le n-1$）：$p_{i,0}{p}_{i,1}\cdots p_{i,n-1}$

输出格式

评测程序示例的输出格式如下：

• 第 $1$ 行: construct 的返回值。

如果 construct 的返回值为 $1$，评测程序示例会额外打印：

• 第 $2+i$ 行（$0\le i\le n-1$）：$b_{i,0}{b}_{i,1}\cdots b_{i,n-1}$

样例一

input

4
1 1 2 2
1 1 2 2
2 2 1 2
2 2 2 1

output

1
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0

explanation

考虑以下调用：

construct([[1, 1, 2, 2], [1, 1, 2, 2], [2, 2, 1, 2], [2, 2, 2, 1]])

这表明从塔 $0$ 到塔 $1$ 恰好有一条路径。对于所有其他的塔对 $(x,y)(0\le x<y\le 3)$, 恰好有两条不同的路径连接塔 $x$ 和塔 $y$。这可以通过建设 $4$ 座桥来实现：连接塔对 $(0,1),(1,2),(1,3)$ 和 $(2,3)$。

为了给出这个解决方案，函数 construct 应该做以下调用：

• build([[0, 1, 0, 0], [1, 0, 1, 1], [0, 1, 0, 1], [0, 1, 1, 0]])

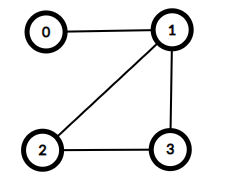
函数应该返回 $1$。

对于这个例子，存在多种不同的建设方案来满足要求，所有这些方案都被认为是正确的。

样例二

input

2
1 0
0 1

output

1
0 0
0 0

explanation

考虑以下调用：

construct([[1, 0], [0, 1]])

这表明无法在两个塔之间进行旅行。这只能通过不建设桥梁来满足。

因此，函数 construct 应该做以下调用：

• build([[0, 0], [0, 0]])

然后，函数 construct 应该返回 $1$。

样例三

input

2
1 3
3 1

output

0

explanation

考虑以下调用：

construct([[1, 3], [3, 1]])

这表明从塔 $0$ 到塔 $1$ 恰好有 $3$ 条路径。这些要求无法满足。因此，函数 construct 应该返回 $0$ 并且不要调用 build。

限制与约定

对于 $100\mathrm{\%}$ 的数据，满足：

• $1\le n\le 1000$
• $p_{i,i}=1$（对所有 $0\le i\le n-1$）
• $p_{i,j}=p_{j,i}$（对所有 $0\le i,j\le n-1$）
• $0\le p_{i,j}\le 3$（对所有 $0\le i,j\le n-1$）

时间限制：$1\mathtt{\text{s}}$

空间限制：$1024\mathtt{\text{MB}}$

下载

样例及测评库下载