【JOISC2020】扫除 - 题目 - Universal Online Judge

比太郎的房间是一个直角边长度为 $N$ 的等腰直角三角形。以直角定点为原点，两条直角边分别为 $x, y$ 轴建立坐标系， $(x, y) (0 \leq x \leq N, 0 \leq y \leq N, x + y \leq N)$ 就表示比太郎房间中的一个点。

比太郎的房间

一天，比太郎注意到他的房间里充满了灰尘。一开始，房间里有 $M$ 片灰尘，其中第 $i$ 片的坐标是 $(X_{i}, Y_{i})$ 。不同的灰尘可以重叠。

现在，比太郎打算用扫帚打扫房间。我们可以把扫帚看作房间里的一条线段，并把线段的长度称作扫帚的宽度。比太郎是一个井井有条的人，他只会按照以下两种方式打扫房间：

比太郎把扫帚放在 $y$ 轴上，使扫帚的一个端点落在原点。然后，他沿着 $x$ 轴的方向水平移动扫帚，直到扫帚碰到房间的斜边为止，保持扫帚的一个端点在 $x$ 轴上，并且与 $y$ 轴平行。如果扫帚的宽度是 $l$ ，原来位于 $(x, y) (x < N - l, y \leq l)$ 的灰尘将会被扫到 $(N - l, y)$ 处。（ $(N - l, y)$ 处可能有其它灰尘。）这被称作过程H。
比太郎把扫帚放在 $x$ 轴上，使扫帚的一个端点落在原点。然后，他沿着 $y$ 轴的方向竖直移动扫帚，直到扫帚碰到房间的斜边为止，保持扫帚的一个端点在 $y$ 轴上，并且与 $x$ 轴平行。如果扫帚的宽度是 $l$ ，原来位于 $(x, y) (x \leq l, y < N - l)$ 的灰尘将会被扫到 $(x, N - l)$ 处。（ $(x, N - l)$ 处可能有其它灰尘。）这被称作过程V。

比太郎的房间中依次发生了 $Q$ 个事件。其中的第 $j$ 个是以下四种中的一种：

给定 $L_{j}$ 或 $(A_{j}, B_{j})$ ，请写一个程序回答比太郎对灰尘坐标的询问。

第一行三个整数 $N, M, Q$

接下来 $M$ 行中的第 $i$ 行为两个整数 $(X_{i}, Y_{i})$

接下来 $Q$ 行每行表示一个操作，含有两个或三个整数。每行的第一个整数 $T_{j}$ 表示操作类型：

对 $T_{j} = 1$ 的每个操作输出一行两个整数，表示比太郎查询的灰尘的 $x, y$ 坐标。

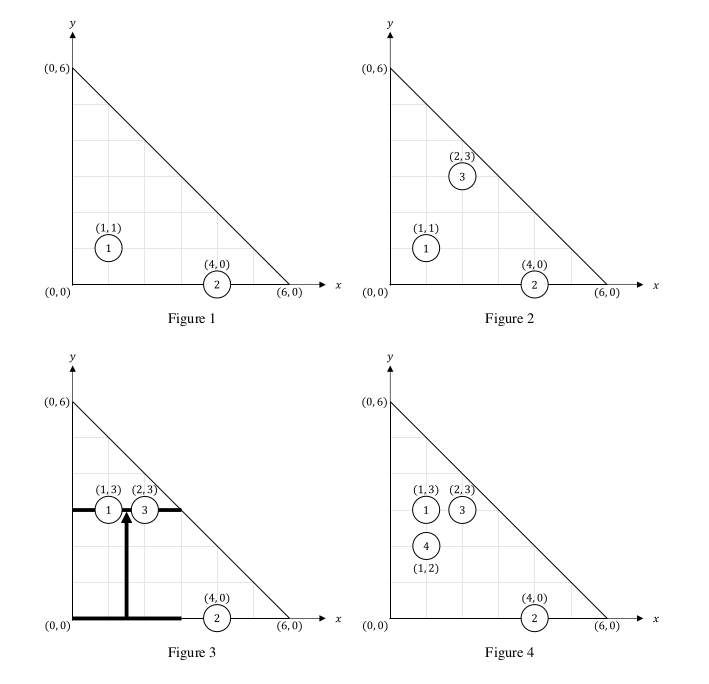
一开始，第一片灰尘落在 $(1, 1)$ ，第二片落在 $(4, 0)$ ，参照图 $1$ 。
在第一个事件中，第三片灰尘出现在 $(2, 3)$ ，参照图 $2$ 。
在第二个事件中，比太郎用宽度为 $3$ 的扫帚进行过程V。第一片灰尘被移动到了 $(1, 3)$ ，参照图 $3$ 。
在第三个事件中，比太郎计算第一片灰尘的坐标 $(1, 3)$ 。
在第四个事件中，第四片灰尘出现在了 $(1, 2)$ 处，参照图 $4$ 。
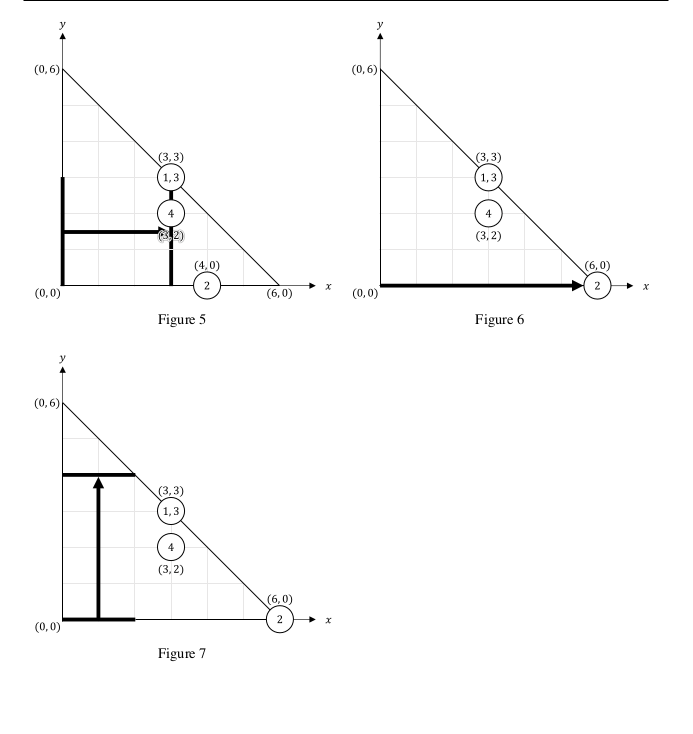
在第五个事件中，比太郎用宽度为 $3$ 的扫帚进行过程H。第一片灰尘的坐标现在是 $(3, 3)$ ，第三片灰尘的坐标现在是 $(3, 3)$ ，第四片灰尘的坐标现在是 $(3, 2)$ ，参照图 $5$ 。
在第六个事件中，比太郎用宽度为 $0$ 的扫帚进行过程H。第二片灰尘被移到了 $(6, 0)$ ，参照图 $6$ 。
在第七个事件中，比太郎计算第 $4$ 片灰尘的坐标 $(3, 2)$ 。
在第八个事件中，比太郎使用宽度为 $2$ 的扫帚进行操作V。没有灰尘被移动，参照图 $7$ 。
在第九个事件中，比太郎计算第三片灰尘的坐标 $(3, 3)$ 。
在第十个事件中，比太郎计算第二片灰尘的坐标 $(6, 0)$ 。

这组测试数据符合子任务 $1, 2, 4, 5$ 的要求。

4 1
3 5
3 2

这组测试数据符合子任务 $1, 2, 5$ 的要求。

( $1$ 分) $M \leq 2000, Q \leq 5000$
( $10$ 分) $T_{j} = 1, 2, 4$
( $11$ 分) $T_{j} = 1, 2, 3, X_{j} \leq X_{j + 1}, Y_{j} \geq Y_{j + 1} (1 \leq j \leq M - 1)$
( $53$ 分) $T_{j} = 1, 2, 3$
( $25$ 分) 没有额外的限制

时间限制: $10S$ 。

空间限制: $1GB$ 。

祝大家一遍 AC，求不虐萌萌哒测评机！

Universal Online Judge