小 S 在和小 F 玩一个叫「斗地主」的游戏。

可怜的小 S 发现自己打牌并打不过小 F，所以他想要在洗牌环节动动手脚。

一副牌一共有 $n$ 张牌，从上到下依次标号为 $1\sim n$。标号为 $i$ 的牌分数是 $f(i)$。在本题，$f(i)$ 有且仅有两种可能：$f(i)=i$ 或 $f(i)=i^2$。

洗牌的方式和我们日常生活中的比较类似，以下我们用形式化的语言来定义：

洗牌环节一共分 $m$ 轮，这 $m$ 轮洗牌依次进行。第 $i$ 轮洗牌时： 1. 小 S 会拿出从最上面往下数的前 $A_i$ 张牌。这样这副牌就被分成了两堆：第一堆是最上面的 $A_i$ 张牌，第二堆是剩下的 $n-A_i$ 张牌，且这两堆牌内相对顺序不变。特别地，当 $A_i=n$ 或 $A_i=0$ 时，有一堆牌是空的。 2. 接下来对两堆牌进行合并，从而产生新的第三堆牌。当第一堆牌还剩下 $X$ 张，第二堆牌还剩下 $Y$ 张的时候，以 $\frac{X}{X+Y}$ 的概率取出第一堆牌的最下面的牌，并将它放入新的第三堆牌的最上面，$\frac{Y}{X+Y}$ 的概率取出第二堆牌的最下面的牌，并将它放入新的第三堆牌的最上面。 3. 重复操作 2，一直取到两堆牌都为空为止。这样我们就完成了一轮洗牌。

因为洗牌过程是随机的，所以小 S 发现自己没法知道某个位置上具体是哪张牌。但小 S 想问你在经历了这 $m$ 轮洗牌后，某个位置上的牌的期望分数是多少。小 S 一共会问你 $Q$ 个这样的问题。

输入格式

从标准输入读入数据。

输入的第一行包含三个正整数 $n,m,\text{type}$，分别表示牌的数量，洗牌的轮数与 $f(i)$ 的类型。当 $\text{type}=1$ 时，$f(i)=i$。当 $\text{type}=2$ 时，$f(i)=i^2$。

接下来一行，一共 $m$ 个整数，表示 $A_1\sim A_m$。

接下来一行一个正整数 $Q$，表示小 S 的询问个数。

接下来 $Q$ 行，每行一个正整数 $c_i$，表示小 S 想要知道从上往下第 $c_i$ 个位置上的牌的期望分数。保证 $1\le c_i\le n$。

输出格式

输出到标准输出中。

输出一共 $Q$ 行，每行一个整数，表示答案在模 $998244353$ 意义下的取值。

即设答案化为最简分式后的形式为 $\frac{a}{b}$，其中 $a$ 和 $b$ 互质。输出整数 $x$ 使得 $bx\equiv a(\text{mod}998244353)$ 且 $0\le x<998244353$。可以证明这样的整数 $x$ 是唯一的。

样例一

input

4 1 1
3
1
1

output

249561090

explanation

有 $\frac{1}{4}$ 的概率从上到下的最终结果是 $\{1,2,3,4\}$。

有 $\frac{1}{4}$ 的概率从上到下的最终结果是 $\{1,2,4,3\}$。

有 $\frac{1}{4}$ 的概率从上到下的最终结果是 $\{1,4,2,3\}$。

有 $\frac{1}{4}$ 的概率从上到下的最终结果是 $\{4,1,2,3\}$。

所以最终有 $\frac{1}{4}$ 的概率第一个位置是 $4$，有 $\frac{3}{4}$ 的概率第一个位置是 $1$，所以第一个位置的期望分数是 $\frac{7}{4}$。

为了帮助你们更直观地了解洗牌的过程，我们在下面画出了结果是 $\{1,4,2,3\}$ 的过程：

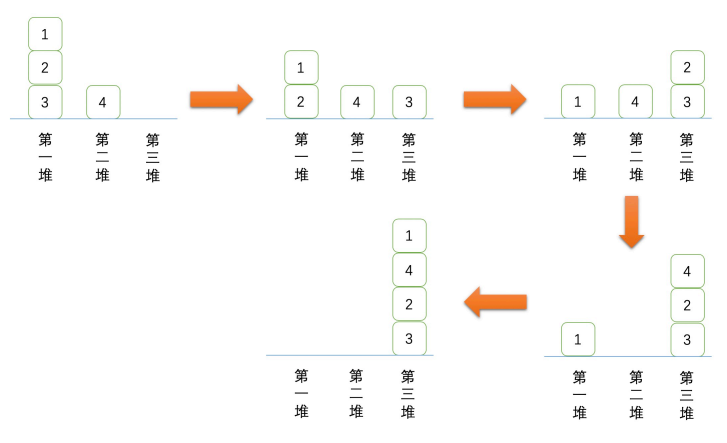
样例二至样例三

见样例数据下载。

限制与约定

对于所有测试数据：$3\le n\le {10}^7,1\le m,Q\le 5\times {10}^5,0\le A_i\le n,\text{type}\in \{1,2\}$。

时间限制: 4s

空间限制: 512MB

下载

样例数据下载