Last night I saw you running

In the open fields of grace

No longer were you broken or in pain

题面中的歌词来自 Jackie Evancho 的 Open Fields of Grace，作曲者为 Lisa Venkatrathnam 和 Paul Sumares。

你找到了一片一望无际的大田野，在这片田野中你忘记了曾经破碎、痛苦的过去。你像小孩一样在上帝的恩赐中奔跑。

然而你发现了一个问题，在这片田野中有若干条峡谷。你随时都有坠入峡谷中的危险。为了继续自由自在的奔跑，你决定用若干围栏将这些峡谷围起来。

我们可以忽视峡谷的宽度，将每一条峡谷看做一条线段。这些线段可以相交，而你的围栏必须是一条或多条闭合不自交且两两不相交的曲线，使得任何一个峡谷都完全在某一条闭合曲线围成的闭合区域之内。

当然，围栏需要消耗资源，消耗的资源和围栏的长度成正比，你希望最小化消耗的资源总量，所以你希望求出围栏总长度的下确界，换句话说，你希望找到一个最大的实数 $x$，使得不存在一个方案使得围栏总长度小于 $x$。

输入格式

输入文件的第一行为一个整数 $n$，表示峡谷的个数。

接下来 $n$ 行，第 $i$ 行四个整数 $a_i,b_i,c_i,d_i$，表示第 $i$ 条峡谷为一条连接点 $(a_i,b_i)$ 和点 $(c_i,d_i)$ 的线段。保证两个端点不重合，不同的线段不会涉及到相同的点。保证任意三点不共线。

输出格式

输出一行一个实数，表示围栏总长度的下确界。你的答案和标准答案的绝对误差和相对误差的最小值不能超过 $10^{−6}$。

样例一

input

1
0 0 0 1

output

2.00000000

explanation

一个四个端点分别为 $(−0.01,−0.01),(−0.01,1.01),(0.01,1.01),(0.01,−0.01)$ 的长方形完全包含输入的线段，且总长度为 $2.08$，略大于下确界。

我们可以证明，不存在长度恰好为 $2$ 的方案。我们可以通过将正方形无限向输入线段“缩紧”来构造一个长度为任意大于 $2$ 的方案。

样例二

input

4
-2 7 -1 7
0 0 0 1
2 -3 5 5
1 0 6 -1

output

23.563573998194637061425470524757

explanation

下图为输入的线段，注意线段可以相交：

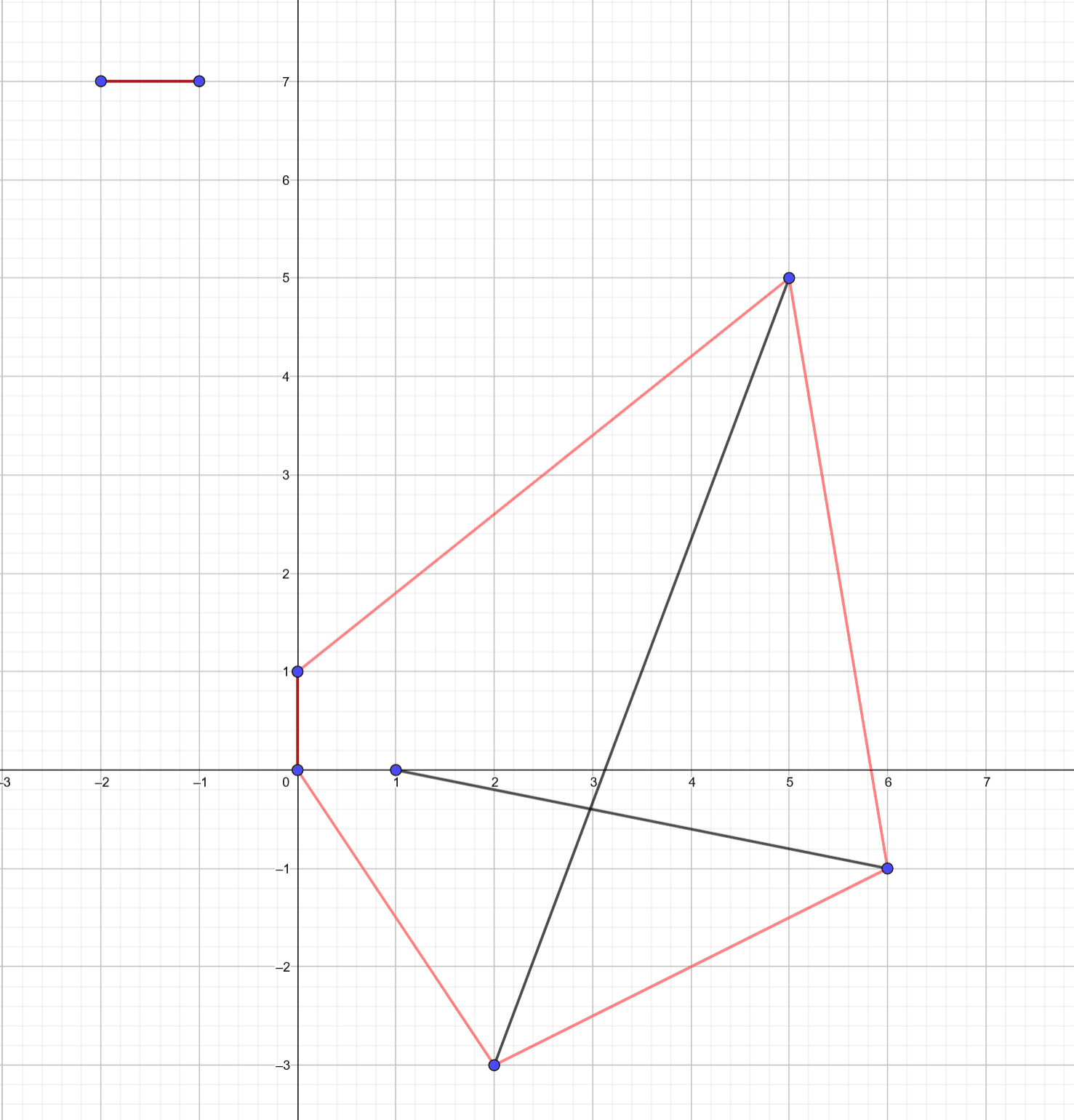
我们以通过无限「逼近」这些红色的曲线来构造任意总长度大于答案的方案。注意通过样例 1，我们很容易知道左上角的红色线段被算了两遍。

样例输入 3

4
-1 1 -1 3
0 4 2 4
3 1 3 3
0 0 2 0

样例三

input

13.656854249492380195206754896839

样例解释 3

答案为 $8+4\sqrt 2$。

explanation

解释如图：

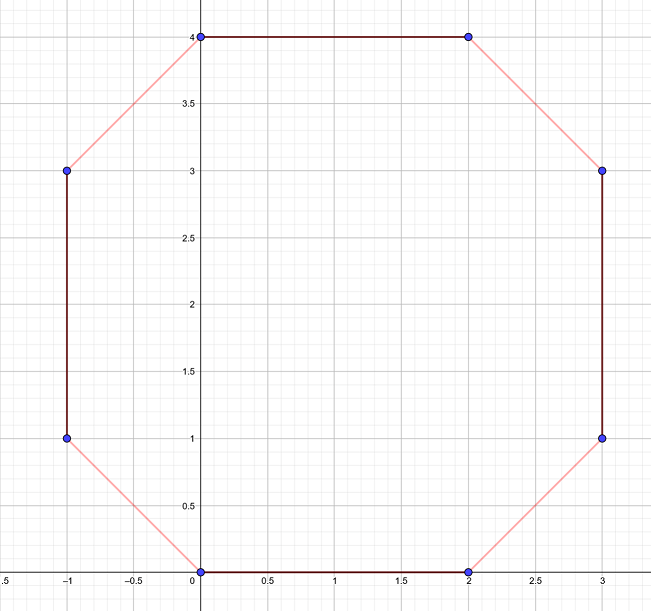
我们可以通过无限「逼近」这些红色的曲线来构造任意总长度大于 $8+4\sqrt 2$ 的方案。

样例四

见样例数据下载。

限制与约定

对于 $5\%$ 的数据，保证 $n = 1$。

对于 $10\%$ 的数据，保证 $1\le n\le 2$。

对于 $15\%$ 的数据，保证 $1\le n\le 10$。

对于 $30\%$ 的数据，保证 $1\le n\le 15$。

对于 $45\%$ 的数据，保证 $1\le n\le 30$。

对于 $55\%$ 的数据，保证 $1\le n\le 60$。

对于 $65\%$ 的数据，保证 $1\le n\le 120$。

对于 $75\%$ 的数据，保证 $1\le n\le 200$。

对于另外 $10\%$ 的数据，保证答案最多包含两条曲线。

对于 $100\%$ 的数据，保证 $1\le n\le 250$，$0\le |a_i|,|b_i|,|c_i|,|d_i|\le 10^9$。

保证两个端点不重合，不同的线段不会涉及到相同的点。保证任意三点不共线。

时间限制: 4s

空间限制: 512MB

下载

样例数据下载

题解

这篇论文中的算法可以用来解决本题。