小 D 特别喜欢玩游戏。这一天，他在玩一款填数游戏。

这个填数游戏的棋盘是一个 $n\times m$ 的矩形表格。玩家需要在表格的每个格子中填入一个数字（数字 $0$ 或者数字 $1$），填数时需要满足一些限制。下面我们来具体描述这些限制。

为了方便描述，我们先给出一些定义：

• 我们用每个格子的行列坐标来表示一个格子，即 $(x,y)$，其中，$x$ 为行坐标，$y$ 为列坐标。（注意：行列坐标均从 $0$ 开始编号）；
• 合法路径 $P$：一条路径是合法的当且仅当：
  1. 这条路径从矩形表格的左上角的格子 $(0,0)$ 出发，到矩形的右下角格子 $(n-1,m-1)$ 结束；
  2. 在这条路径中，每次只能从当前的格子移动到右边与它相邻的格子，或者从当前格子移动到下面与它相邻的格子。

例如：在下面这个矩形中，只有两条路径是合法的，它们分别是 $P_1:(0,0)\to (0,1)\to (1,1),P_2:(0,0)\to (1,0)\to (1,1)$。

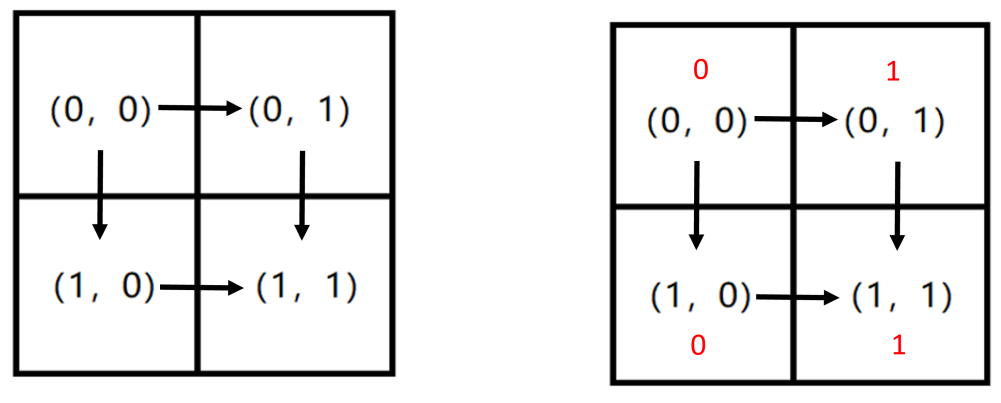
对于一条合法的路径 $P$，我们可以用一个字符串 $w(P)$ 来表示，该字符串的长度为 $n+m-2$，其中只包含字符 R 或者字符 D，第 $i$ 个字符记录了路径 $P$ 中第 $i$ 步的移动方法，R 表示移动到当前格子右边与它相邻的格子，D 表示移动到当前格子下面与它相邻的格子。例如，上图中对于路径 $P_1$，有 $w(P_1)=‘‘\text{RD}"$；而对于另一条路径 $P_2$，有 $w(P_2)=‘‘\text{DR}"$。

同时，将每条合法路径 $P$ 经过的每个格子上填入的数字依次连接后，会得到一个长度为 $n+m-1$ 的 $01$ 字符串，记为 $s(P)$。例如，如果我们在格子 $(0,0)$ 和 $(1,0)$ 上填入数字 $0$，在格子 $(0,1)$ 和 $(1,1)$ 上填入数字 $1$（见上图红色数字）。那么对于路径 $P_1$，我们可以得到 $s(P_1)=‘‘011"$，对于路径 $P_2$，有 $s(P_2)=‘‘001"$。

游戏要求小 D 找到一种填数字 $0,1$ 的方法，使得对于两条路径 $P_1,P_2$，如果 $w(P_1)>w(P_2)$，那么必须 $s(P_1)\le s(P_2)$。我们说字符串 $a$ 比字符串 $b$ 小，当且仅当字符串 $a$ 的字典序小于字符串 $b$ 的字典序，字典序的定义详见第一题。但是仅仅是找一种方法无法满足小 D 的好奇心，小 D 更想知道这个游戏有多少种玩法，也就是说，有多少种填数字的方法满足游戏的要求？

小 D 能力有限，希望你帮助他解决这个问题，即有多少种填 $0,1$ 的方法能满足题目要求。由于答案可能很大，你需要输出答案对 ${10}^9+7$ 取模的结果。

输入格式

输入文件，包含两个正整数 $n,m$，由一个空格分隔，表示矩形的大小。其中 $n$ 表示矩形表格的行数，$m$ 表示矩形表格的列数。

输出格式

输出共一行，包含一个正整数，表示有多少种填 $0,1$ 的方法能满足游戏的要求。

注意：输出答案对 ${10}^9+7$ 取模的结果。

样例一

input

2 2

output

12

样例说明 1

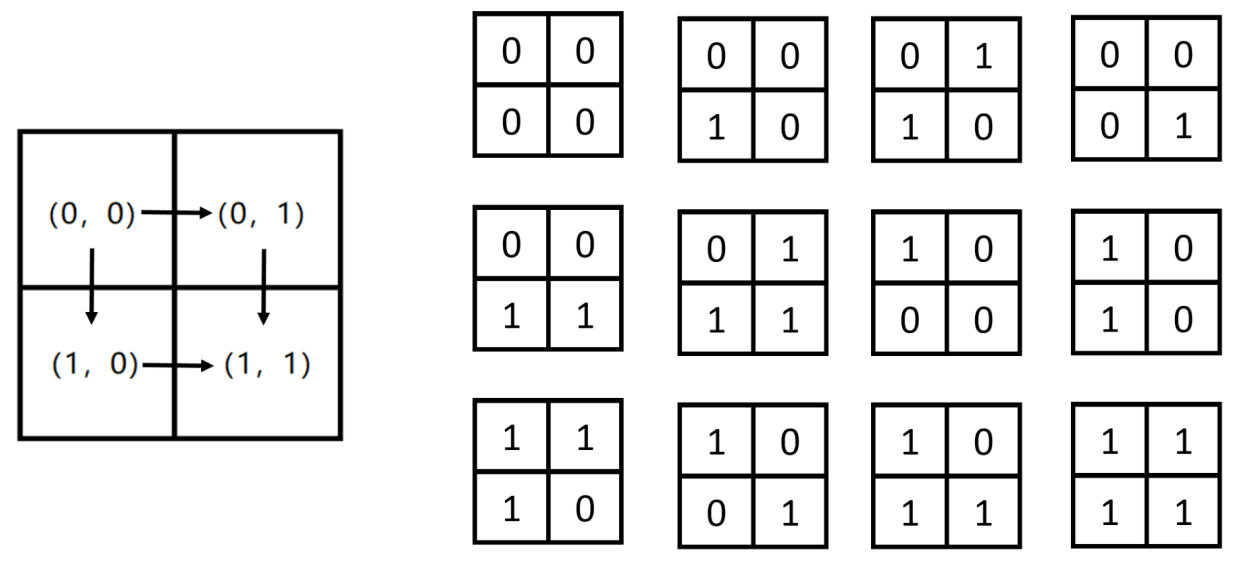
对于 $2\times 2$ 棋盘，有上图所示的 $12$ 种填数方法满足要求。

样例二

input

3 3

output

112

样例三

input

5 5

output

7136

限制与约定

对于所有子任务均满足 $1\le n,m$。

时间限制：$\mathtt{\text{1s}}$。

空间限制：$\mathtt{\text{512MB}}$。

下载

样例数据下载