在平面上，有 $n$ 个圆，记为 $c_1,c_2,\dots ,c_n$ 。我们尝试对这些圆运行这个算法：

• 找到这些圆中半径最大的。如果有多个半径最大的圆，选择编号最小的。记为 $c_i$ 。
• 删除 $c_i$ 及与其有交集的所有圆。两个圆有交集当且仅当平面上存在一个点，这个点同时在这两个圆的圆周上或圆内。（原文直译：如果平面上存在一个点被这两个圆所包含，我们称这两个圆有交集。一个点被一个圆包含，当且仅当它位于圆内或圆周上。）
• 重复上面两个步骤直到所有的圆都被删除。

当 $c_i$ 被删除时，若循环中第1步选择的圆是 $c_j$ ，我们说 $c_i$ 被 $c_j$ 删除。对于每个圆，求出它是被哪一个圆删除的。

输入格式

第一行包含一个整数 $n$ ，表示开始时平面上圆的数量 ($1\le n\le 3\cdot {10}^5$)。

接下来 $n$ 行，每行包含三个整数 $x_i,y_i,r_i$ 依次描述圆 $c_i$ 圆心的x坐标、y坐标和它的半径 ($-{10}^9\le x_i,y_i\le {10}^9$, $1\le r_i\le {10}^9$)。

输出格式

输出一行，包含 $n$ 个整数 $a_1,a_2,...a_n$ ，其中 $a_i$ 表示圆 $c_i$ 是被圆 $c_{a_i}$ 删除的。

样例一

input

11
9 9 2
13 2 1
11 8 2
3 3 2
3 12 1
12 14 1
9 8 5
2 8 2
5 2 1
14 4 2
14 14 1

output

7 2 7 4 5 6 7 7 4 7 6

explanation

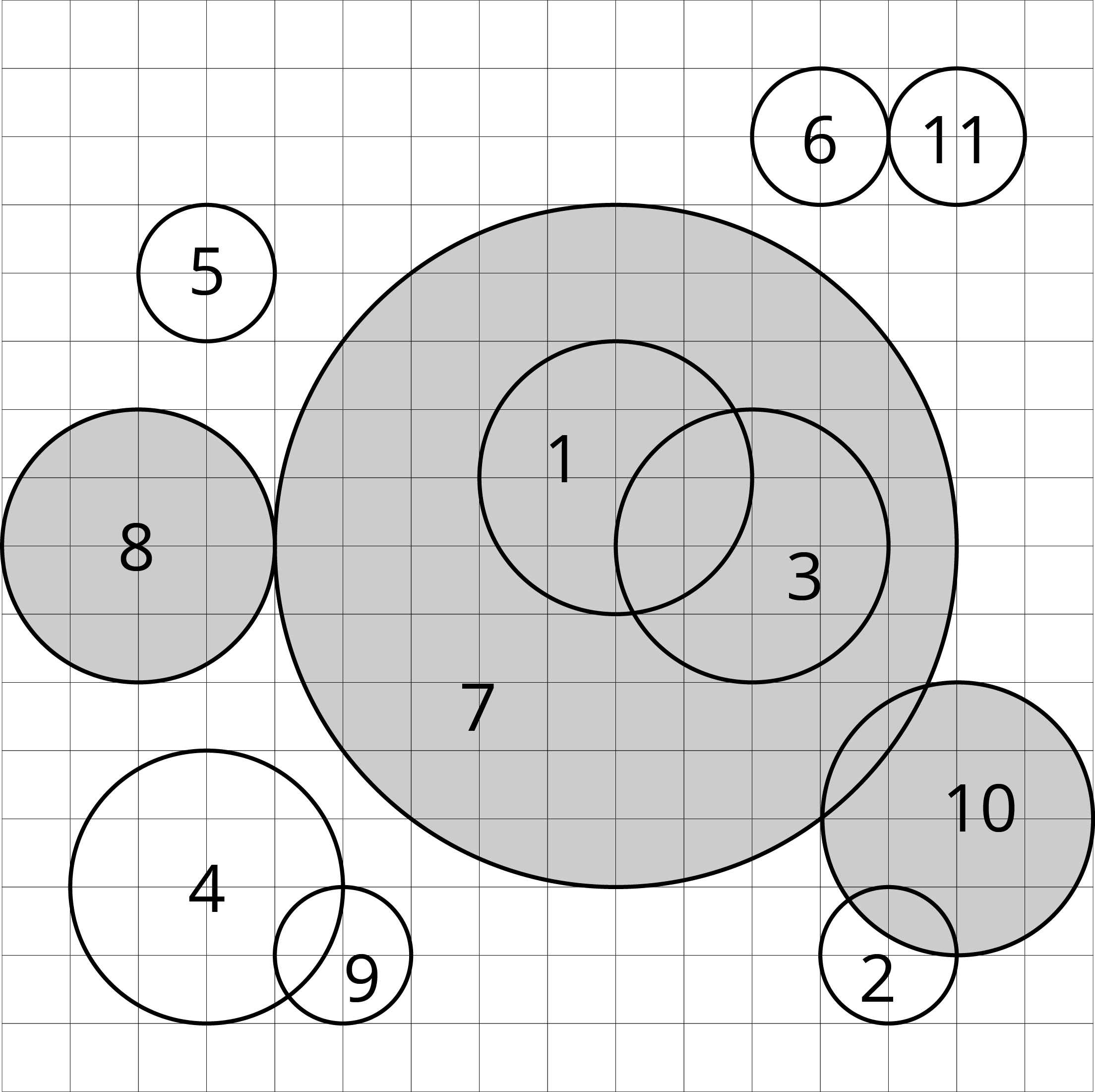
题目描述中的图片对应了样例一中的情形。

限制与约定

子任务 1（7 分）：$n\le 5000$

子任务 2（12 分）：$n\le 3\cdot {10}^5$, 对于所有的圆 $y_i=0$

子任务 3（15 分）：$n\le 3\cdot {10}^5$, 每个圆最多和一个其他圆有交集。

子任务 4（23 分）：$n\le 3\cdot {10}^5$, 所有的圆半径相同。

子任务 5（30 分）：$n\le {10}^5$

子任务 6（13 分）：$n\le 3\cdot {10}^5$

时间限制：$3s$

空间限制：$1024MB$

下载

样例数据下载