有 $N$ 座山横着排成一行，从左到右编号为从 $0$ 到 $N-1$。山 $i$ 的高度为 $H_i$（ $0\le i\le N-1$ ）。每座山的顶上恰好住着一个人。

你打算举行 $Q$ 个会议，编号为从 $0$ 到 $Q-1$。会议 $j$（ $0\le j\le Q-1$ ）的参加者为住在从山 $L_j$ 到山 $R_j$（包括 $L_j$ 和 $R_j$ ）上的人（ $0\le L_j\le R_j\le N-1$ ）。对于该会议，你必须选择某个山 $x$ 做为会议举办地（ $L_j\le x\le R_j$ ）。举办该会议的成本与你的选择有关，其计算方式如下：

• 来自每座山 $y$（ $L_j\le y\le R_j$ ）的参会者的成本，等于在山 $x$ 和 $y$ 之间（包含 $x$ 和 $y$ ）的所有山的最大高度。特别地，来自山 $x$ 的参会者的成本是 $H_x$，也就是山 $x$ 的高度。
• 会议的成本等于其所有参会者的成本之和。

你想要用最低的成本来举办每个会议。

注意，所有的参会者将在每次会议后回到他们自己的山；所以一个会议的成本不会受到先前会议的影响。

实现细节

你需要实现下面的函数：

int64[] minimum_costs(int[] H, int[] L, int[] R)

• H：长度为 $N$ 的数组，表示这些山的高度。
• L和R：两个长度为 $Q$ 的数组，表示这些会议的参会者的范围。
• 该函数应返回一个长度为 $Q$ 的数组 $C$。 $C_j$（ $0\le j\le Q-1$ ）必须是举办会议 $j$ 的最低的可能成本。
• 注意，$N$ 和 $Q$ 的值是数组的长度，可以按照注意事项中的相关内容来取得。

例子

设 $N=4$，$H=[2,4,3,5]$，$Q=2$，$L=[0,1]$ 和 $R=[2,3]$。

评测程序调用minimum_costs([2, 4, 3, 5], [0, 1], [2, 3])。

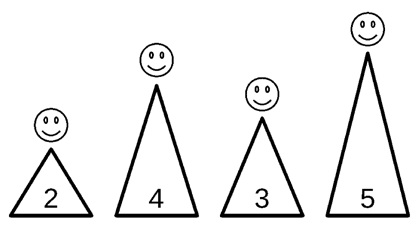
会议 $j=0$ 有 $L_j=0$ 和 $R_j=2$，所以将由住在山 $0$、$1$ 和 $2$ 上的人参加。如果山 $0$ 被选做举办地，会议的成本计算如下：

• 住在山 $0$ 上的参会者的成本是 $max\{H_0\}=2$。
• 住在山 $1$ 上的参会者的成本是 $max\{H_0,H_1\}=4$。
• 住在山 $2$ 上的参会者的成本是 $max\{H_0,H_1,H_2\}=4$。
• 因此，会议 $0$ 的成本是 $2+4+4=10$。

不可能以更低的成本来举办会议 $0$ 了，因此会议 $0$ 的最低成本是 $10$。

会议 $j=1$ 有 $L_j=1$ 和 $R_j=3$，因此将由住在山 $1$、$2$ 和 $3$ 上的人参加。如果山 $2$ 被选做举办地，会议的成本计算如下：

• 住在山 $1$ 上的参会者的成本是 $max\{H_1,H_2\}=4$。
• 住在山 $2$ 上的参会者的成本是 $max\{H_2\}=3$。
• 住在山 $3$ 上的参会者的成本是 $max\{H_2,H_3\}=5$。
• 因此，会议 $1$ 的成本是 $4+3+5=12$。

不可能以更低的成本来举办会议 $1$ 了，所以会议 $1$ 的最低成本是 $12$。

在样例数据下载中的文件ex_meetings1.in和ex_meetings1.out对应于本例。在样例包中还可找到其他样例输入/输出。

限制条件

• $1\le N\le 750000$
• $1\le Q\le 750000$
• $1\le H_i\le 1000000000(0\le i\le N-1)$
• $0\le L_j\le R_j\le N-1(0\le j\le Q-1)$
• $(L_j,R_j)\ne (L_k,R_k)(0\le j<k\le Q-1)$

子任务

1. (4 分) $N\le 3000,Q\le 10$
2. (15 分) $N\le 5000,Q\le 5000$
3. (17 分) $N\le 100000,Q\le 100000,H_i\le 2(0\le i\le N-1)$
4. (24 分) $N\le 100000,Q\le 100000,H_i\le 20(0\le i\le N-1)$
5. (40 分) 没有附加限制

评测程序示例

评测程序示例读取如下格式的输入数据：

• 第 $1$ 行：$NQ$
• 第 $2$ 行：$H_{0}H-1\cdots H_{N-1}$
• 第 $3+j$ 行（ $0\le j\le Q-1$ ）：$L_j{R}_j$

评测程序示例将以如下格式输出minimum_costs的返回值：

• 第 $1+j$ 行（ $0\le j\le Q-1$ ）：$C_j$

约定及限制

对于所支持的各种编程语言，下面列出了对应的数据类型。对于数据类型的细节等，参见实现示例。

时间限制：$5\mathtt{\text{s}}$

空间限制：$805\mathtt{\text{MB}}$

下载

样例数据下载