所谓机械娃娃，是能够自动地重复特定运动序列的娃娃。在日本，很多机械娃娃在古代就造出来了。机械娃娃的运动被一个由多个器件组成的管路所控制。这些器件通过管道连在一起。每个器件都有一个或两个出口，而且可以有任意多的（也可以为零）的入口。每个管道都从某个器件的出口连到同一器件或其他器件的入口。每个入口都连接恰好一个管道，而每个出口也都连接恰好一个管道。

为了描述娃娃是如何运动的，设想有一个球放在这些器件之一的上面。这个球在管路中穿行。在穿行的每一步，它从所在器件的一个出口离开该器件，沿着连接该出口的管道，进入管道另一头所连接的器件。

器件有三种类型：起点、 触发器和开关。总共有恰好一个起点，$M$ 个触发器和 $S$ 个开关（$S$ 可以为零）。开关的数量 $S$ 要由你来定。每个器件都有唯一的序列号。

起点是球最初所在的那个器件。它有一个出口。它的序列号是 $0$。

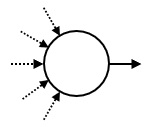
一旦球进入某个触发器，就会让娃娃做某个特定运动。每个触发器都有一个出口。触发器的序列号是从 $1$ 到 $M$。

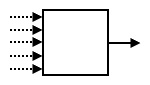
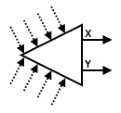
每个开关都有两个出口，被记为“X”和“Y”。开关的状态或者为“X”，或者为“Y”。在球进入 某个开关后，它会从开关的当前状态所对应的出口离开。此后开关将切换为另一状态。最初，所有开 关的状态都是“X”。开关的序列号是从$-1$到$-S$。

告诉你触发器的数量 $M$。再给你一个长度为 $N$ 的序列 $A$，序列的每个元素都是某个触发器的序列号。每个触发器会在序列 $A$ 中出现若干次（也可能是零次）。你的任务是设计一个管路，以满足如下条件：

• 球在若干步之后返回到起点。
• 当球首次返回到起点时，所有开关的状态都是“X”。
• 在球首次返回到起点时，此前它进入所有触发器的总次数恰好为 $N$。这些被进入过的触发器，其序列号按照被球经过的顺序依次为$A_0,A_1,\dots ,A_{N-1}$。
• 设 $P$ 为球首次返回到起点时，球所引起的所有开关状态切换的总次数。$P$ 不能超过 $2\times {10}^7$。

同时，你不要用太多的开关。

实现细节

你需要实现下面的过程。

create_circuit(int M, int[] A)

• M：触发器数量。
• A：长度为 $N$的数组，其中按照球进入的顺序，给出了被进入的触发器的序列号。
• 该过程将被调用恰好一次。
• 注意，$N$ 的值是数组 $A$ 的长度，你可以按照注意事项中的有关内容来取得。

你的程序需要调用下面的过程来作答。

answer(int[] C, int[] X, int[] Y)

• C：长度为 $M+1$ 的数组。器件 $i$（ $0\le i\le M$ ）的出口被连到器件C[i]。
• X, Y：长度相同的两个数组。这些数组的长度 $S$ 为开关的数量。对于开关 $-j$（ $1\le j\le S$ ）来说，其出口“X”被连到器件X[j - 1]，而出口“Y”被连到器件Y[j - 1]。
• C、X和Y中的任一元素必须是 $-S$ 到 $M$ 的整数（包括 $-S$ 和 $M$）。
• $S$ 最多只能是 $400000$。
• 必须调用该过程恰好一次。
• 由C、X和Y所表示的管路必须满足题面中的限制条件。

如果上述条件不满足，你的程序将被判为 $\mathtt{\text{Wrong Answer}}$。否则，你的程序将被判为 $\mathtt{\text{Accepted}}$，而你的得分将根据 $S$ 来计算（参见子任务）。

例子

假设 $M=4$，$N=4$ 和 $A=[1,2,1,3]$。评测程序调用create_circuit(4, [1, 2, 1, 3])。

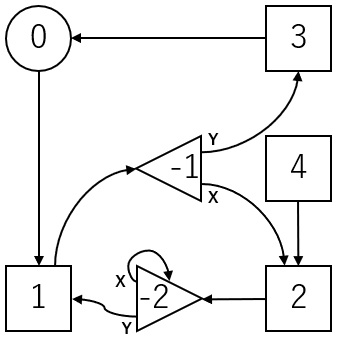
上图展示了函数调用answer([1, -1, -2, 0, 2], [2, -2], [3, 1])所对应的管路图。图中的数字是器件的序列号。

图中使用了两个开关。所以$S=2$.

开关 $-1$ 和 $-2$ 的初始状态都是“X”。

球的穿行轨迹如下：

$$0\to 1\to -1\stackrel{\mathtt{\text{X}}}{\to }2\to -2\stackrel{\mathtt{\text{X}}}{\to }-2\stackrel{\mathtt{\text{Y}}}{\to }1\to -1\stackrel{\mathtt{\text{Y}}}{\to }3\to 0$$

当球首次进入开关 $-1$ 时，该开关的状态为“X”。所以，该球走到触发器 $2$。然后开关 $-1$ 的状态变成“Y”。

当球第二次进入开关 $-1$ 时，该开关的状态为“Y”。所以，该球走到触发器 $3$。然后开关 $-1$的状态变为“X”。

球在经过触发器 $1,2,1,3$ 后首次返回到起点。开关 $-1$ 和 $-2$ 的状态都是“X”。$P$的值是 。所以，这个管路是满足条件的。

在压缩附件包中，有一个文件 sample-01-in.txt 对应于本例。其他输入样例也可以在压缩附件包中找到。

在样例数据下载中的文件ex_doll1.in对应于本例。其他的输入样例在样例包中还可找到。注意：样例包中的输出没有任何意义。

限制条件

• $1\le M\le 100000$
• $1\le N\le 200000$
• $1\le A_k\le M(0\le k\le N-1)$

子任务

每个测试样例的分数和限制条件如下：

1. （2 分）对每个 $i$ ( $1\le i\le M$ )，整数 $i$ 在序列 $A_0,A_1,\dots A_{N-1}$ 中最多出现 $1$ 次。
2. （4 分）对每个 $i$ ( $1\le i\le M$ )，整数 $i$ 在序列 $A_0,A_1,\dots A_{N-1}$ 中最多出现 $2$ 次。
3. （10 分）对每个 $i$ ( $1\le i\le M$ )，整数 $i$ 在序列 $A_0,A_1,\dots A_{N-1}$ 中最多出现 $4$ 次。
4. （10 分）$N=16$
5. （18 分）$N=18$
6. （56 分）无附加限制

对每个测试样例，如果你的程序被判定为 $\mathtt{\text{Accepted}}$，你的得分将根据 $S$ 的值来计算：

• 如果 $S\le N+{\log }_{2}N$，你将获得该测试样例的满分。
• 对于子任务 $5$ 和 $6$ 的每个测试样例，如果 $N+{\log }_{2}N<S\le 2N$，你将获得部分分。该测试样例上的得分为 $0.5+0.4\times {\left(\frac{2N-S}{N-{\log }_{2}N}\right)}^2$，再乘以该子任务的满分分数。
• 否则，得分为 $0$。

注意，你在每个子任务上的得分是该子任务中所有测试样例上的最低得分。

请注意：在测试中，如果你的程序在一个子任务中某个点未获得满分，则可能会得到 $0$ 分。

评测程序示例

评测程序示例按照以下格式从标准输入中读入输入：

• 第 $1$ 行：$MN$
• 第 $2$ 行：$A_0{A}_1\dots A_{N-1}$

评测程序示例产生三个输出。

首先，评测程序示例把你的答案以下列格式输出到文件out.txt。

• 第 $1$ 行：$S$
• 第 $2+i$ 行（ $0\le i\le M$ ）：C[i]
• 第 $2+M+j$ 行（ $1\le j\le S$ ）：X[j - 1] Y[j - 1]

其次，评测程序示例模拟球的移动。它把该球经过的器件的序列号，按照经过顺序输出到文 件log.txt。

第三，评测程序示例将在标准输出中打印对你的答案的评价

• 如果你的程序被判为 $\mathtt{\text{Accepted}}$，评测程序示例按照以下格式打印 $S$ 和 $P$：$\mathtt{\text{Accepted: S P}}$
• 如果你的程序被判为 $\mathtt{\text{Wrong Answer}}$，它打印 $\mathtt{\text{Wrong Answer: MSG}}$。各类 $\mathtt{\text{MSG}}$ 的含义如下：
  • answered not exactly once：过程 answer 不是恰好被调用一次。
  • wrong array length：C的长度不是 $M+1$，或者X和Y的长度不一样。
  • over 400000 switches：$S$ 大于 $400000$。
  • wrong serial number：C、X或者 Y 的某个元素比 $-S$ 小或者比 $M$ 大。
  • over 20000000 inversions：球没有在所有开关的状态变化总数超过 $20000000$ 之前返回到起点。
  • state 'Y'：当球首次返回到起点时，某个开关的状态为“Y”。
  • wrong motion：触发运动的触发器和序列$A$所列的不一致。

注意，当你的程序被判为 $\mathtt{\text{Wrong Answer}}$ 时，评测程序示例可能并不创建out.txt和/或log.txt。

约定及限制

对于所支持的各种编程语言，下面列出了对应的数据类型。对于数据类型的细节等，参见实现示例。

时间限制：$1\mathtt{\text{s}}$

空间限制：$268\mathtt{\text{MB}}$

下载

样例数据下载