C 国和 D 国近年来战火纷飞。

最近，C 国成功地渗透进入了 D 国的一个城市。这个城市可以抽象成一张有 $n$ 个节点，节点之间由 $n-1$ 条双向的边连接的无向图，使得任意两个点之间可以互相到达， 也就是说这张无向图实际上是一棵树。

经过侦查，C 国情报部部长 GGB 惊讶地发现，这座看起来不起眼的城市竟然是 D 国的军事中心。因此 GGB 决定在这个城市内设立情报机构。情报专家 TAC 在侦查后，安排了 $m$ 种设立情报机构的方案。这些方案中，第 $i$ 种方案是在节点 $x_i$ 到节点 $y_i$ 的最短路径的所有边上安排情报人员收集情报，这种方案需要花费 $v_i$ 元的代价。

但是，由于人手不足，GGB 只能安排上述 $m$ 种方案中的两种进行实施。同时 TAC 指出，为了让这两个情报机构可以更好的合作，它们收集情报的范围应至少有一条公共的边。为了评估一种方案的性能，GGB 和 TAC 对所有的边进行了勘察，给每一条边制定了一个情报价值 $c_i$，表示收集这条边上的情报能够带来 $c_i$ 元的收益。注意，情报是唯一的，因此当一条边的情报被两个情报机构收集时，也同样只会有 $c_i$ 的收益。

现在，请你帮 GGB 选出两种合法的设立情报机构的方案进行实施，使得这两种方案收集情报的范围至少有一条公共的边，并且在此基础上总收益减去总代价的差最大。

注意，这个值可能是负的，但仍然是合法的。如果无法找到这样的两种方案，请输出 F。

输入格式

从标准输入读入数据。

本题包含多组测试数据。

输入文件的第一行包含一个整数 $T$，表示数据组数；

每组数据包含 $(n+m+1)$ 行：

第 $1$ 行包含一个整数 $n$，表示城市的点数；

第 $2$ 到第 $n$ 行中，第 $(i+1)$ 行包含三个整数 $a_i$，$b_i$，$c_i$，表示城市中一条连接节点 $a_i$ 和 $b_i$、情报价值为 $c_i$ 的双向边，保证 $a_i<b_i$ 且 $b_i$ 互不相同；

第 $(n+1)$ 行包含一个整数 $m$，表示 TAC 设立的 $m$ 种设立情报机构的方案；

第 $(n+2)$ 到 $(n+m+1)$ 行中，第 $(n+i+1)$ 行包含三个整数 $x_i$，$y_i$，$v_i$，表示第 $i$ 种设立情报机构的方案是在节点 $x_i$ 到节点 $y_i$ 的最短路径上的所有边上安排情报人员收集情报，并且需要花费 $v_i$ 元的代价。

保证节点的编号是从 $1$ 至 $n$ 的，且 $1\le a_i,b_i,x_i,y_i\le n$。

输出格式

输出到标准输出中。

输出文件包含 $T$ 行；

对于每组数据，输出一行：如果存在合法的方案，则输出一个整数表示最大的总收益减去总代价的差；否则输出 F。

样例一

input

2
5
1 2 1
2 3 3
3 4 2
1 5 8
2
1 4 5
3 5 8
5
1 2 1
2 3 3
3 4 3
1 5 9
2
1 5 5
2 3 8

output

1
F

explanation

这个样例中包含两组数据。这两组数据的城市相同，只是在情报的价值和情报机构的方案上有所不同。城市地图如下：

• 对于第一组数据，方案一中的节点 $1$ 到节点 $4$ 的最短路径为 $1\to 2\to 3\to 4$，方案二中的节点 $3$ 到节点 $5$ 的最短路径为 $3\to 2\to 1\to 5$。选择这两种方案需要花费 $5+8=13$ 的代价，并且每一条边的情报都被收集从而得到 $1+3+2+8=14$ 的收益，因此总收益减去总代价为 $14-13=1$。
• 对于第二组数据，方案一中的节点 $1$ 到节点 $5$ 的最短路径为 $1\to 5$，方案二中的节点 $2$ 到节点 $3$ 的最短路径为 $2\to 3$。这两种方案收集情报的范围没有公共的边，因此非法，所以这组数据不存在合法方案，应输出 F。

样例二

见下载文件中的 ex_center2.in 与 ex_center2.ans。 这个样例只包含一组数据。这一数据中，最优方案为选择第 $2$ 种和第 $3$ 种方案。

这组数据的城市地图如下，其中加粗的边表示被情报中心收集情报的边，红色的边表示只被第 $2$ 种方案的情报中心收集情报的边，蓝色的边表示只被第 $3$ 种方案的情报中心收集情报的边，紫色的边表示同时被两个情报中心收集情报的边。

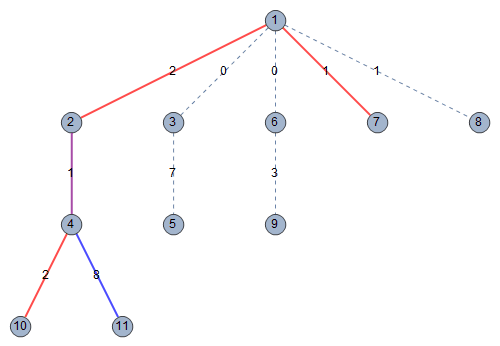
样例三

见下载文件中的 ex_center3.in 与 ex_center3.ans。

这个样例和第 $4$ 个测试点的性质相同。每个测试点的性质见下文的表格。

样例四

见下载文件中的 ex_center4.in 与 ex_center4.ans。

这个样例包含了经过特殊构造的 $n\le 100,m\le 200$ 的测试数据，涵盖了测试点中所有出现性质的组合。你可以合理利用这个测试点，对自己的程序进行全面的检查。

这个样例，无疑是善良的出题人无私的馈赠。大量精心构造的 $n\le 100,m\le 200$ 的测试数据，涵盖了测试点中所有出现性质的组合。你可以利用这个测试点，对自己的程序进行全面的检查。足量的数据组数、不大的数据范围和多种多样的数据类型，能让程序中的错误无处遁形。出题人相信，这个美妙的样例，可以给拼搏于 AC 这道题的逐梦之路上的你，提供一个有力的援助。

限制与约定

各测试点的数据规模和性质如下表：

表格中的特殊性质如下：

• 特殊性质 $S_1$：对于任意 $i,j$，保证 $x_i$ 到 $y_i$ 的最短路径所经过的编号最小的节点不同于 $x_j$ 到 $y_j$ 的最短路径所经过的编号最小的节点；
• 特殊性质 $S_2$：对于任意 $i$，保证 $x_i$ 到 $y_i$ 的最短路径所经过的编号最小的节点为节点 $1$。

对于所有的数据，$1\le n\le 5\times {10}^4$，$0\le m\le {10}^5$，$0\le c_i\le {10}^9$，$0\le v_i\le {10}^{10}\times n$。每个测试点中，所有 $n$ 的和不会超过 $1,000,233$，所有 $m$ 的和不会超过 $2,000,233$。

时间限制：$8\mathtt{\text{s}}$

空间限制：$512\mathtt{\text{MB}}$

下载

样例数据下载