九条可怜是一个热爱出题的女孩子。
今天可怜想要出一道和图论相关的题。在一张无向图
- 它的点集大小为
- 两个点之间有边当且仅当这两个点对应的边在原图上有公共点(注意不会有自环)。
下图是一个简单的例子,左图是原图,右图是它对应的线图。其中点
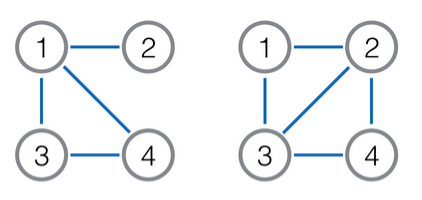
经过一些初步的摸索,可怜发现线图的性质要比补图复杂很多,其中突出的一点就是补图的补图会变回原图,而
因此,可怜想要从最简单的入手,即计算
然而遗憾的是,即使是这个问题,对可怜来说还是太困难了,因此她进行了一定的弱化。她给出了一棵
输入格式
第一行输入两个整数
接下来
输出格式
输出一行一个整数,表示答案对
样例一
input
5 3 1 2 2 3 2 5 3 4
output
5
explanation
如下图所示,左图为原树,中图为
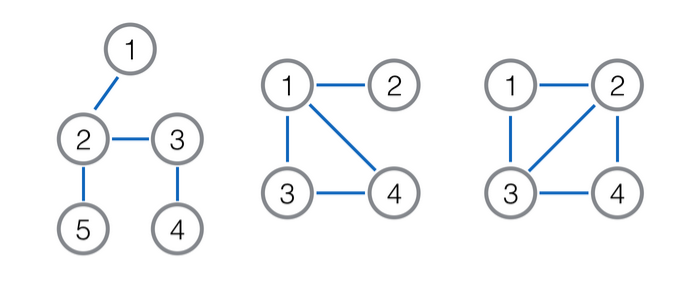
样例二
见样例数据下载
数据范围与约定
| 测试点 | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
时间限制:
空间限制:

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号