JOI 岛是一个观光胜地，全岛被定为一个自然公园。

JOI 岛有 $N$ 个广场和若干条道路。广场从 $0$ 至 $N - 1$ 编号。每条道路联结岛内两个不同的广场，可以双向通行。对于每一个广场，至多有 $7$ 条道路将它与其他广场相连。对于任意两个不同的广场，至多有 $1$ 条道路将它们相连。此外，我们已知任意两个广场都可以通过若干条道路互相到达。

你和你的朋友 IOI 酱决定考察 JOI 岛。为了考察能够高效进行，你不得不掌握全岛的结构。岛上的诸多动物会带来危险，因此由运动细胞发达的 IOI 酱去探索全岛，而你则负责基于 IOI 酱的报告来确定岛的结构。

你可以对 IOI 酱指定两个广场 $A$、$B$，以及若干可以经过的广场，向其询问是否可以只经由指定的广场从 $A$ 到达 $B$。IOI 酱会按照询问的内容在岛上探索并报告结果。

请编写一个程序与 IOI 酱交流并确定 JOI 岛的完整结构。由于考察不能持续过长时间，需要将询问次数限制在 $45\,000$ 次以内。

实现细节

本题仅支持 C/C++ 语言。

你需要实现一个过程来确定岛的结构。请包含头文件 park.h。

程序需要实现以下过程。

• void Detect(int T, int N)
  • 此函数只会被调用 $1$ 次。
  • 参数 $\texttt{T}$ 表示子任务编号，$\texttt{N}$ 表示广场的数目。

程序中需要调用以下函数来输出所确定的 JOI 岛的构造。

• void Answer(int A, int B)
  • 此函数被调用的次数须等于 JOI 岛的道路数目。
  • 参数 $\texttt{A}$ 和 $\texttt{B}$ 表示确定了一条联结广场 $\texttt{A}$ 和 $\texttt{B}$ 的道路。
  • 参数需要满足以下条件：
    • $\texttt{A}$ 和 $\texttt{B}$ 须满足 $0 \leq \texttt{A} < \texttt{B} \leq N - 1$。不满足此条件时，会被判为 Wrong Answer [1]。
    • 对于一组参数 $(\texttt{A}, \texttt{B})$，广场 $\texttt{A}$ 与广场 $\texttt{B}$ 之间须有一条道路。不满足此条件时，会被判为 Wrong Answer [2]。
    • 对于一组参数 $(\texttt{A}, \texttt{B})$ 不得调用 $2$ 次及以上。不满足此条件时，会被判为 Wrong Answer [3]。

此外，程序中可以调用如下函数。

• int Ask(int A, int B, int Place[])
  • 此函数用于向 IOI 酱提出询问。
  • $\texttt{Place}$ 指向表示每个广场是否可以经过的数组。对于每个 $\texttt{i}$（$0 \leq \texttt{i} \leq N - 1$），$\texttt{Place[i]} = 1$ 表示可以经过广场 $i$，$\texttt{Place[i]} = 0$ 表示不可以经过广场 $i$。
  • 此函数的返回值在可以只经由允许的广场从广场 $A$ 到达广场 $B$ 的情况下返回 $1$，不能到达的情况下返回 $0$。
  • 参数需要满足以下条件：
    • $0 \leq \texttt{A} < \texttt{B} \leq N - 1$。
    • $0 \leq \texttt{Place[i]} \leq 1$（$0 \leq \texttt{i} \leq N - 1$）。
    • $\texttt{Place[A]} = 1$。
    • $\texttt{Place[B]} = 1$。
  • 不满足这些条件时，会被判为 Wrong Answer [4]。另外，数组 $\texttt{Place[]}$ 的长度不足 $N$ 时的行为是未定义的。
  • 此外，函数 $\texttt{Ask}$ 被调用的次数不能超过 $45\,000$ 次。超过的情况下，会被判为 Wrong Answer [5]。

函数 $\texttt{Detect}$ 结束时，若存在未被作为过函数 $\texttt{Answer}$ 调用参数的道路，被判为 Wrong Answer [6]。

为了内部使用而定义的其他函数及全局变量不作限制。但是，你的提交不应该向标准输入/输出或者其他文件进行任何读写操作。

测试程序方式

「附加文件」中提供了 park.h、grader.c 和 grader.cpp 三个文件。若你编写的程序名称为 park.c 或 park.cpp，请运行以下命令来编译：

• C 语言 gcc -std=c11 -O2 -o grader grader.c park.c -lm

• C++ 语言 g++ -std=c++14 -O2 -o grader grader.cpp park.cpp

当命令成功时，会产生一个可执行文件 grader。

注意实际评测时的程序与下发的样例评测程序并不相同。实际的 park.h 函数实现将通过标准输入/输出与单独运行的交互器进行交互。

样例评测程序输入格式

样例评测程序将从标准输入读入以下数据。

• 第 $1$ 行一个整数 $T$，表示子任务编号。

• 第 $2$ 行一个整数 $N$，表示广场有 $N$ 个。

• 第 $3$ 行一个整数 $M$，表示道路有 $M$ 条。

• 接下来 $M$ 行中的第 $i$（$1 \leq i \leq M$）行包含两个空格分隔的整数 $A_i, B_i$，表示有一条联结广场 $A_i$ 与广场 $B_i$ 的双向道路。

样例评测程序输出格式

样例评测程序将向标准输出输出以下信息。

• 判为正确时，输出 Accepted；

• 运行过程中被判为错误时，以 Wrong Answer [x] 的格式报告并退出。

程序执行过程中违反了多种限制时，只会报告其中的一种。

样例一

input (grader)

1
6
7
0 1
0 3
1 2
1 4
2 4
2 5
3 4

interaction

注意本样例中的函数调用可能并无实际意义。

本样例中，函数 $\texttt{Detect}$ 以参数 $\texttt{T} = 1, \texttt{N} = 6$ 被调用。

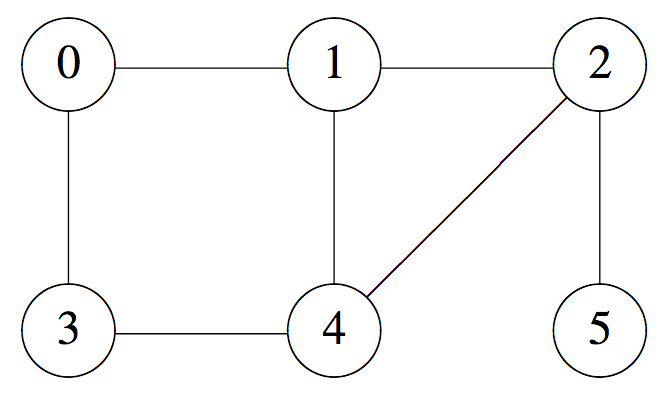
本样例中，JOI 岛的结构如下图所示。

• 第 $1$ 次调用函数 $\texttt{Ask}$ 时，允许经过广场 $2, 3, 4, 5$，询问从广场 $3$ 是否可以到达广场 $5$。由于可以到达，函数 $\texttt{Ask}$ 返回 $1$。

• 第 $2$ 次调用函数 $\texttt{Ask}$ 时，允许经过广场 $0, 2, 4$，询问从广场 $0$ 是否可以到达广场 $4$。由于不可以到达，函数 $\texttt{Ask}$ 返回 $0$。

数据范围与提示

所有数据满足下列条件。$T$，$N$，$M$ 的含义参照「样例评测程序输入格式」一节。

• $1 \leq T \leq 5$。

• $2 \leq N \leq 1\,400$。

• $1 \leq M \leq 1\,500$。

• 对于任意一个广场，至多有 $7$ 条道路将它与其他广场联结。

• 对于任意两个不同广场，可以通过若干道路互相到达。

• 对于任意两个不同广场，联结它们的道路至多有 $1$ 条。

子任务数据满足下列条件。

子任务 1（10 分）

• $T = 1$。

• $N \leq 250$。

子任务 2（10 分）

• $T = 2$。

• $M = N - 1$。

• 对于广场 $0$ 与广场 $N - 1$，只有 $1$ 条道路将它们与其他广场相连。对于其他广场，恰有 $2$ 条道路将它们与其他广场相连。

子任务 3（27 分）

• $T = 3$。

• $M = N - 1$。

• 对于任意一个 $i$（$1 \leq i \leq N - 1$），至多经由 $8$ 个其他广场即可从广场 $0$ 到达广场 $i$。

子任务 4（30 分）

• $T = 4$。

• $M = N - 1$。

子任务 5（23 分）

• $T = 5$。

时间限制：$2\texttt{s}$

空间限制：$256\texttt{MB}$