现有一块大奶酪，它的高度为 $h$，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为 $z = 0$，奶酪的上表面为 $z = h$。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑到奶酪的上表面去?

空间内两点 $P_1(x_1,y_1,z_1)$、$P_2(x_2,y_2,z_2)$ 的距离公式如下：

$$\mathrm{dist}(P_1,P_2) = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$$

输入格式

每个输入文件包含多组数据。

输入文件的第一行，包含一个正整数 $T$，代表该输入文件中所含的数据组数。

接下来是 $T$ 组数据，每组数据的格式如下：

第一行包含三个正整数 $n$，$h$ 和 $r$，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。

接下来的 $n$ 行，每行包含三个整数 $x$、$y$、$z$，两个数之间以一个空格分开，表示空洞球心坐标为 $(x,y,z)$ 。

输出格式

输出文件包含 $T$ 行，分别对应 $T$ 组数据的答案，如果在第 $i$ 组数据中，Jerry 能从下表面跑到上表面，则输出“Yes”，如果不能，则输出“No”（均不包含引号）。

样例一

input

3
2 4 1
0 0 1
0 0 3
2 5 1
0 0 1
0 0 4
2 5 2
0 0 2
2 0 4

output

Yes
No
Yes

explanation

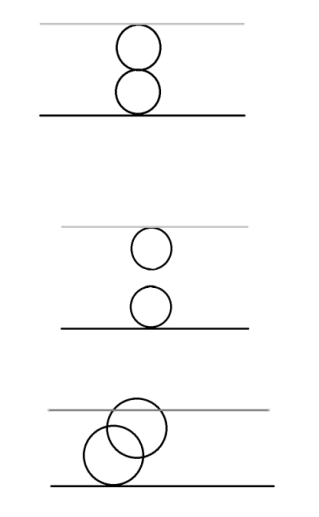
下面三个图分别是第一、二、三组数据的剖面图。

第一组数据中，第一个空洞在 $(0,0,0)$ 与下表面相切，第二个空洞在 $(0,0,4)$ 与上表面相切，两个空洞在 $(0,0,2)$ 相切。输出 Yes。

第二组数据中，两个空洞既不相交也不相切，输出 No。

第三组数据中，两个空洞相交，且与上下表面相切或相交，输出 Yes。

样例二

见样例数据下载。

限制与约定

对于 $20\%$ 的数据，$n = 1$，$1 \le h , r \le 10,000$，坐标的绝对值不超过 $10,000$。

对于 $40\%$ 的数据，$1 \le n \le 8$， $1 \le h , r \le 10,000$，坐标的绝对值不超过 $10,000$。

对于 $80\%$ 的数据，$1 \le n \le 1,000$，$1 \le h , r \le 10,000$，坐标的绝对值不超过 $10,000$。

对于 $100\%$ 的数据，$1 \le n \le 1,000$，$1 \le h , r \le 1,000,000,000$，$T \le 20$，坐标的绝对值不超过 $1,000,000,000$。

时间限制：$1\texttt{s}$

空间限制：$256\texttt{MB}$

下载

样例数据下载