德黑兰市是伊朗国家图书馆的所在地。这个图书馆的镇馆之宝位于一个长长的大厅内，大厅里有排成一行的 $n$ 张桌子，从左到右依次编号为从 $0$ 到 $n-1$。每张桌子上都陈列着一本手写的古书。这些古书是根据其历史年份进行排序的，这使得访客们难以根据书名来查找它们。所以，图书馆主管决定按照书名的字母序来重新排列它们。

图书管理员 Aryan 要完成这项工作。他创建了一个长度为 $n$ 的列表 $p$，其中包括由 $0$ 到 $n-1$ 的不同整数。这个列表描述了按字母序来重排古书所要做的改变：对于 $0\leq i< n$，目前在桌子 $i$ 上的古书应该被移到桌子 $p[i]$ 上。

Aryan 从桌子 $s$ 开始重排这些古书。他希望在做完重排工作之后再回到同一张桌子上。由于这些古书非常珍贵，在任何时间，他手持的古书都不能超过一本。在重排古书的过程中，Aryan 将会做一系列的操作。每个操作只能是以下其中之一：

• 如果他手上没有书，而他所在的桌子上恰好有一本书时，他可以拿起这本书。
• 如果他手上有一本书，而他所在的桌子上恰好有另一本书时，他可以把手上的书和桌子上的书进行交换。
• 如果他手上有一本书，而他所在的桌子上没有书时，他可以把手上的书放到这个桌子上。
• 他可以走到任何一张桌子前。当他进行这个操作时，他手上可以拿一本书。

对于所有 $0\leq i,j\leq n-1$，桌子 $i$ 和桌子 $j$ 之间的距离正好是 $|j-i|$ 米。你的任务是，计算出 Aryan 重排好所有古书所走过的总距离的最小值。

实现细节

本题只支持C++。

你需要实现下面的函数：

 long long minimum_walk(std::vector<int> p, int s)

$p$ 是一个长度为 $n$ 的数组。初始阶段在桌子 $i$ 上的古书需要被 Aryan 移到桌子 $p[i]$ 上（对于所有 $0\leq i < n$）。

$s$ 是初始阶段 Aryan 所在桌子的编号，同时也是重排好所有古书之后他应该在的位置。

该函数要返回 Aryan 重排好所有古书所需走过的总距离的最小值（以米为单位）。

例子

评测程序调用 minimum_walk([0, 2, 3, 1], 0)。

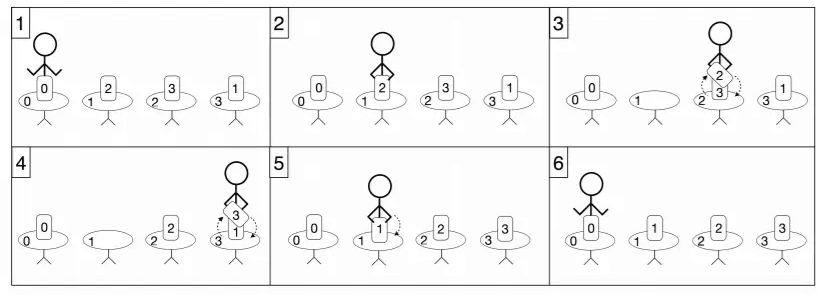
在这个例子中，$n=4$，在初始阶段Aryan位于桌子 $0$ 处。他按照如下步骤进行重排：

• 走到桌子 $1$ 处并且拿起桌上的书。这本书应该要被放到桌子 $2$ 上。
• 然后，他走到桌子 $2$ 处，并且把他手上的书和桌子上的书进行交换。现在他新拿到手上的书应该被放到桌子 $3$ 上。
• 然后，他走到桌子 $3$ 处，并且把他手上的书和桌子上的书进行交换。现在他新拿到手上的书应该被放到桌子 $1$ 上。
• 然后，他走到桌子 $1$ 处，并且把他手上的书放到桌子上。
• 最后，他回到桌子 $0$ 处。 注意，桌子 $0$ 上的书已经在正确的位置，即桌子 $0$ 上，因此 Aryan 不需要把它拿起来。在这个方案中，他的总行走距离是 $6$ 米。这是一个最优解；因此，函数应该返回 $6$。

数据范围

• $1\leq n\leq 1 \ 000\ 000$
• $0\leq s\leq n-1$
• 数组 $p$ 包含 $n$ 个从 $0$ 到 $n-1$（含）的不同整数。

时间限制：$1\texttt{s}$

空间限制：$256\texttt{MB}$

评分程序样例

评分程序样例将读入下述格式的输入数据：

• 第 $1$ 行：$n\ s$
• 第 $2$ 行：$p[0]\ p[1]\ \cdots\ p[n-1]$

评分程序样例将输出一行，其中包括 minimum_walk 的返回值。

下载

样例数据与样例评测库下载