“大奖”是一个家喻户晓的TV游戏节目。这次你很幸运地进入到最后一轮。已知编号从 $0$ 到 $n-1$ 的 $n$ 个盒子从左到右排成一行，你就站在这排盒子的前面。每个盒子里面放有一个奖品，必须打开盒子才能看到是什么奖品。已知有 $v\ge 2$ 种不同类型的奖品。这 $v$ 种类型按照奖品价值的降序从 $1$ 到 $v$ 排列。

类型 $1$ 的奖品是一块钻石，价值最高。所有盒子加起来刚好只有一块钻石。类型 $v$ 的奖品是一块棒棒糖，价值最低。为使得游戏更加激动人心，相对便宜的奖品数量远比价值昂贵的奖品数量要多。更具体一点，对于满足 $2\le t\le v$ 的所有 $t$，我们有：如果类型 $t-1$ 的奖品有 $k$ 个，那么类型 $t$ 的奖品将严格多于 $k^2$ 个。

你的目标是赢得那块钻石。在游戏结束时，你必须打开一个盒子并收取盒子内的奖品。在选择要打开的盒子之前，你可以向节目主持人Rambod提一些问题。在每一个问题中，你选择就某个 $i$ 号盒子进行提问。Rambod将给你一个包含两个整数的数组 $a$ 作为回答。这两个整数的意义如下：

• 在 $i$ 号盒子左面的盒子中，刚好有 $a[0]$ 个盒子中的奖品，价值比 $i$ 号盒子中的奖品价值要高。
• 在 $i$ 号盒子右面的盒子中，刚好有 $a[1]$ 个盒子中的奖品，价值比 $i$ 号盒子中的奖品价值要高。

例如，假设 $n=8$，在你的问题中，你选择就 $i=2$ 号盒子进行提问。Rambod的回答是 $a=[1,2]$。这 个回答的意义是：

• $0$ 号盒子和 $1$ 号盒子中恰好有一个盒子中的奖品比 $2$ 号盒子中的奖品更贵。
• 在 $3,4,...,7$ 号盒子中恰好有 $2$ 个盒子中的奖品比 $2$ 号盒子中的奖品更贵。

你的任务就是通过问少量的问题找出包含钻石的盒子。

实现细节

本题只支持C++。

你应当实现如下函数段:

 int find_best(int n)

• 此函数只被评测程序调用仅一次。
• $n$: 盒子的数量.
• 你实现的这个函数应该返回装有钻石的盒子编号，即，唯一的整数 $d$（$0\le d\le n-1$）使得 $d$ 号盒子放有类型为 $1$ 的奖品。

上述函数可以调用下列函数:

 std::vector<int> ask(int i)

• $i$: 你在询问时选择的盒子编号。$i$ 的数值必须介于 $0$ 和 $n-1$ 之间（含）。
• 这个函数返回包含 $2$ 个元素的数组 $a$。其中，$a[0]$ 是在 $i$ 号盒子的左面，奖品比 $i$ 号盒子的奖品价值更高的盒子数目。而 $a[1]$ 则是在 $i$ 号盒子右面，奖品比 $i$ 号盒子的奖品价值更高的盒子数目。

例子

评测工具将做如下函数调用: find_best(8)。

这里有 $n=8$ 个盒子。假定奖品类型为 $[3,2,3,1,3,3,2,3]$。对函数 ask 的所有可能的调用以及相应的返回值列出如下：

• ask(0) 返回 $[0,3]$
• ask(1) 返回 $[0,1]$
• ask(2) 返回 $[1,2]$
• ask(3) 返回 $[0,0]$
• ask(4) 返回 $[2,1]$
• ask(5) 返回 $[2,1]$
• ask(6) 返回 $[1,0]$
• ask(7) 返回 $[3,0]$

在这个例子中, 钻石放在 $3$ 号盒子里。所以函数 find_best 应该返回 $3$。

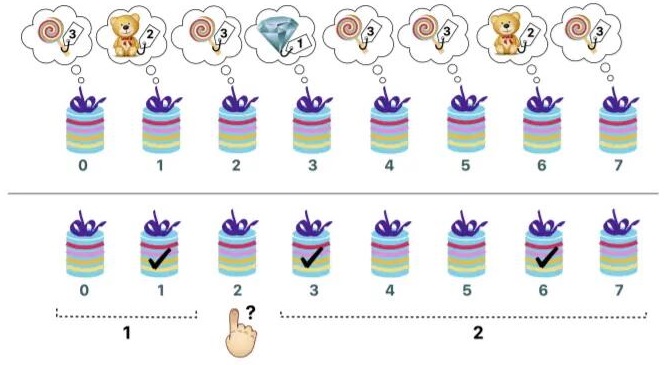
上图阐释了这个例子。图中上半部分给出了每个盒子中奖品的类型。图中的下半部分阐释了询问 ask(2)。做了标记（打$\surd$）的盒子中装有比 $2$ 号盒子的奖品价值更高的奖品。

数据范围

• $3\leq n\leq 200000$
• 每个盒子中奖品的类型介于 $1$ 和 $n$ 之间（含）。
• 类型 $1$ 的奖品恰有一个。
• 对于所有 $2\leq t\leq v$，如果类型 $t-1$ 的奖品有 $k$ 个，那么类型 $t$ 的奖品将严格多于 $k^2$ 个。

在某些测试数据中，评测工具的行为是自适应的。这意味着在这些测试数据中评测工具并没有一个固定的奖品序列。取而代之的是，由评测工具给出的答案可能依赖于你的程序问过的问题。评测工具的回答方式可以保证，在每次回答之后，至少有一个奖品序列与到目前为止给出的所有回答都不冲突。

在子任务 $2$ 中你可以获得部分分。令 $q$ 是在这个子任务的所有测试数据上函数 ask 被调用的最大次数，那么你在这个子任务上的得分将按照下表计算：

时间限制：$1\texttt{s}$

空间限制：$1024\texttt{MB}$

评分程序样例

评分程序样例不是自适应的。取而代之的是，它只是读取并使用一个固定的奖品类型的数组 $p$。对于所有的 $0\leq b\leq n-1$，$b$ 号盒子中的奖品类型将由 $p[b]$ 给出。评测工具示例期望的输入格式如下：

• 第 $1$ 行：$n$
• 第 $2$ 行：$p[0]\ p[1]\ \cdots\ p[n-1]$

评分程序样例输出单独一行，其中包含 find_best 的返回值以及调用函数 ask 的次数。

下载

样例数据与样例评测库下载