Maryam 是一位电机工程师。她正在为一座通讯塔设计接线方案。在这个塔上有一些分布在不同高度的连接点。一条电线可以用来将任何两个连接点接起来。每一个连接点都可以接上任意数目的电线。而连接点共有两种：分别为红色连接点及蓝色连接点。

为了表述方便起见，通讯塔会被视为一条直线，而那些红色及蓝色连接点会被视为在这条直线上的一些非负整数坐标。一条电线的长度是该电线所连接的两个连接点间的距离。

你要做的是帮 Maryam 找出一个接线的方案，使得满足以下条件：

1. 每个连接点上最少有一条电线连接到一个不同颜色的连接点上
2. 所用的电线的总长度为最短。

实现细节

本题只支持C++。

你需要实现以下的子程序：

 long long min_total_length(std::vector<int> r, std::vector<int> b)

• $r$: 一个长度为 $n$ 的数组，其内以升序排列着所有红色连接点的位置。
• $b$: 一个长度为 $m$ 的数组，其内以升序排列着所有蓝色连接点的位置。
• 这个子程序需返回在所有可能的连接方案中，最短电线总长度的那个方案的电线总长度作为其返回值。
• 请注意这个子程序的返回值的类型为 long long。

例子

评测程序调用了 min_total_length([1, 2, 3, 7], [0, 4, 5, 9, 10])。

以下的图表述了样例中的数据。

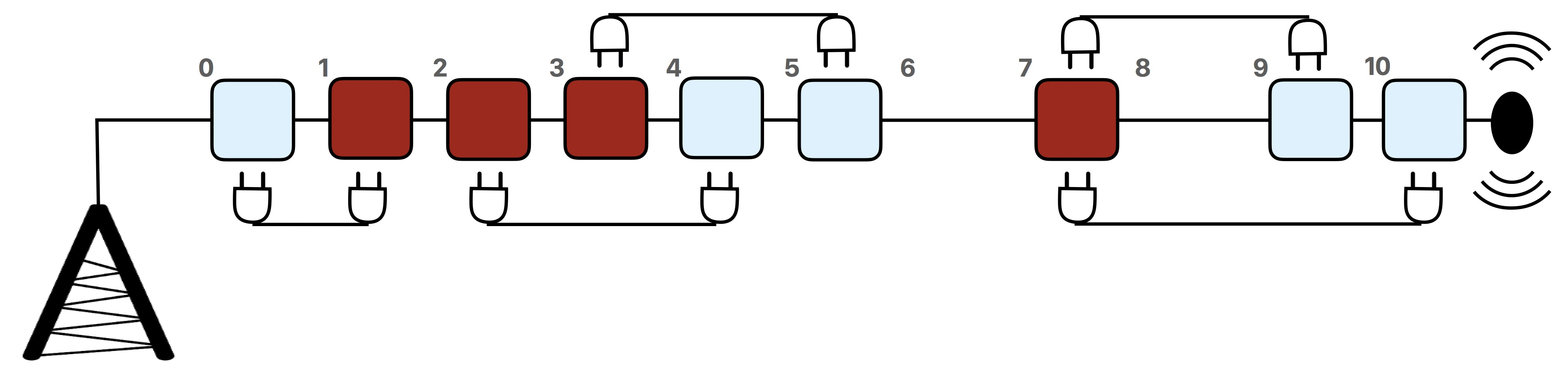
• 图中以水平的方式表示出相关的通讯塔。
• 因题目打印是黑白色的，所以红色接点以较深色来表示，而蓝色接点以较浅色来表示。
• 图中有 $4$ 个红色的连接点，其位置分别为 $1,2,3$ 及 $7$。
• 图中有 $5$ 个蓝色的连接点，其位置分别为 $0,4,5,9$ 及 $10$。
• 该例的最优解的电线总长度为 $1+2+2+2+3=10$，所以子程序的返回值为 $10$。
• 注意共有两条电线连接在位置为 $7$ 的连接点上。

数据范围

• $1\le n,m\le 100000$
• $0\le r[i]\le {10}^9$（对于所有 $0\le i\le n-1$）
• $0\le b[i]\le {10}^9$（对于所有 $0\le i\le m-1$）
• 数组 $r$ 及 $b$ 都已经按升序排好序。
• 在数组 $r$ 及 $b$ 的所有 $n+m$ 个值均是不同的。

时间限制：$1\mathtt{\text{s}}$

空间限制：$256\mathtt{\text{MB}}$

评分程序样例

评分程序样例将会读入以下格式的数据：

• 第 $1$ 行：$n,m$
• 第 $2$ 行：$r[0]r[1]...r[n-1]$
• 第 $3$ 行：$b[0]b[1]...b[m-1]$

评分程序样例将会输出单独一行数据，上面含有 min_total_length 的返回值。

下载

样例数据与样例评测库下载