现在的ac程序应该靠谱。。欢迎大家hack（这个题现在标程挂了。。哪位哥哥愿意提供一下靠谱的标程呀？）

"分！身！术！" —— 小P

平面上有 $n$ 个小P的分身。定义一组分身占领的区域为覆盖这组分身的最小凸多边形。小P能力有限，每一时刻都会有若干分身消失。但在下一时刻之前，小P会使用

"分！身！术！"

使得这些消失的分身重新出现在原来的位置。小P想知道，每一时刻分身消失后，剩下的分身占领的区域面积是多少？

输入格式

从标准输入读入数据。

输入第一行包含两个正整数 $n, m$，描述初始时分身的个数，和总时刻数。

接下来 $n$ 行，第 $i$ 行有两个整数 $x_i, y_i$ ，描述第 $i$ 个分身的位置。

接下来 $m$ 行，每行的第一个整数 $k$ 表示这一时刻有 $k$ 个分身消失。接下来有 $k$ 个非负整数 $c_1,c_2,\cdots c_k$，用于生成消失的分身的编号。

生成方式如下：

设上一个时刻中，分身占领面积的两倍为 $S$。则该时刻消失的分身 $p_{1}, p_{2}, \dots, p_{k}$ 的编号为：

$$p_i = [(S + c_i) ~\mathrm{mod}~ n] + 1$$

特别的，在第一个时刻，我们认为上一个时刻中， $S=-1$ ，即：第一个时刻消失的分身 $p_{1}, p_{2}, \dots, p_{k}$ 的编号为：

$$p_i = [(-1+c_i) ~\mathrm{mod}~ n] + 1$$

输出格式

输出到标准输出。

按给出时刻的顺序依次输出 $m$ 行，每行一个整数，表示该时刻剩余分身所占领区域面积的两倍。

样例一

input

6 2
-1 0
-1 -1
0 -1
1 0
0 1
0 0
3 1 3 6
2 0 1

output

3
2

explanation

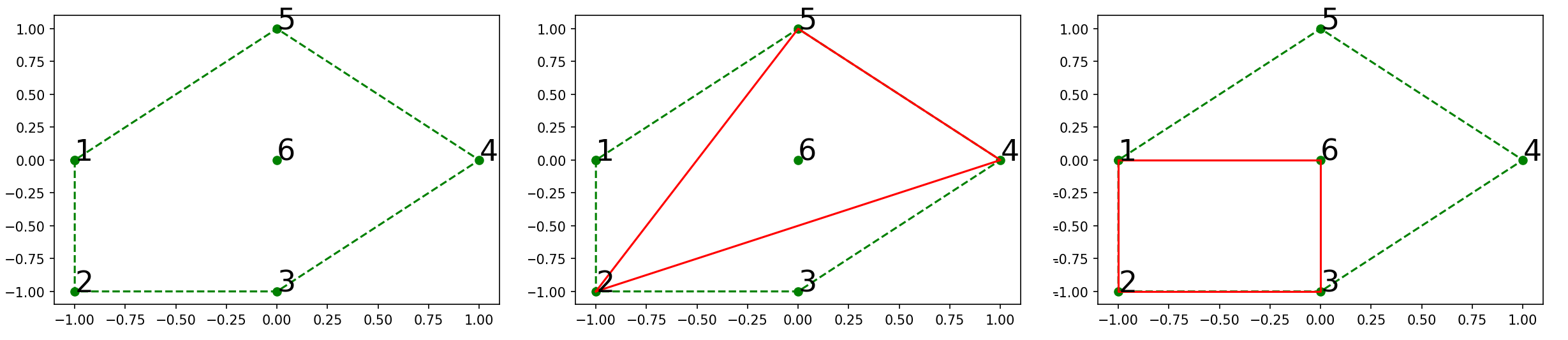
如下图所示：左图表示输入的6个分身的位置及它们占领的区域；中图表示第一个时刻的情形，消失的分身编号分别为 1,3,6，剩余3个点占领图中实线内部区域，占据面积的两倍为 3；右图表示第二个时刻的情形，消失的分身编号分别为 $$[(0+3) ~\mathrm{mod}~ 6] + 1 = 4$$ $$[(1+3) ~\mathrm{mod}~ 6] + 1 = 5$$

剩余的4个点占领图中实线内部区域。

样例二

见“样例数据下载”

样例三

见“样例数据下载”

样例四

见“样例数据下载”

限制与约定

对于所有数据，保证：

• $|x_i|, |y_i|\leq 10^{8}$；
• 没有两个分身的坐标是完全相同的；
• $k \leq 100$；
• 所有时刻的 $k$ 之和不超过 $2 \times 10^{6}$；
• $0 \leq c_i \leq 2^{31}-1$；
• 初始时，所有的 $n$ 个分身占据区域面积大于 $0$；
• 定义所有 $n$ 个分身所占据区域的顶点集合为 $S$， $|S|\geq 3$。在任意时刻，$S$ 中至少存在两个未消失的分身。

时间限制：$3\texttt{s}$

空间限制：$512\texttt{MB}$

下载

样例数据下载