我们的卫星刚刚通过观测一个遥远的星球发现了外星文明。我们也已经获得了该星球的一个正方形区域的低分辨率照片。这个照片上有许多智能生命的迹象。专家们也已经确定了照片上的 $n$ 个兴趣点。这些兴趣点被编号为 $0$ 到 $n - 1$。现在我们希望拍摄一些能包含全部 $n$ 个兴趣点的高分辨率照片。

卫星已将低分辨率照片的区域划分成由 $m \times m$ 个单位正方形的小方格组成的网络。网格的行和列被连续地编号为 $0$ 到 $m - 1$（从上到下和从左到右）。我们用坐标 $(s, t)$ 来表示第 $s$ 行与第 $t$ 列上的小方格。第 $i$ 个兴趣点位于小方格 $(r_i, c_i)$ 上，每个小方格子上可以包含任意多个兴趣点。

卫星在一个固定的轨道上运行，而它刚好也直接经过这个网格的主对角线的上方。主对角线就是指在网络中连接左上角和右下角的那条线段。卫星能够在任意的区域上拍摄高分辨率的照片，但必须满足以下条件：

• 拍摄的区域必须是正方形。
• 这个正方形的两个对角（注：变通理解为主对角线）全部包含在网格的主对角线中。
• 网格中的每个小方格或者完全在拍摄范围内，或者完全在拍摄范围外。

卫星最多只能拍摄 $k$ 张高分辨率照片。

一旦卫星拍摄完成，它将把每个拍摄区域的高分辨率照片传送到地面基站（无论这些区域是否包含兴趣点）。尽管一个小方格可能会被多次拍摄，但每个被拍摄到的小方格上的数据只会被传送一次。

因此，我们必须选择最多 $k$ 个正方形区域进行拍摄，而且要保证：

• 每个包含至少一个兴趣点的小方格必须被至少拍摄到一次，并且
• 被拍摄到至少一次的小方格数目必须是最小的。

你的任务就是去找出被拍摄到的小方格有可能的最小值。

实现细节

你应该实现下列函数（方法）：

• long long take_photos(int n, int m, int k, std::vector<int> r, std::vector<int> c)
  • $n$：兴趣点的数目，
  • $m$：网格中的行数（也是列数），
  • $k$：卫星能够拍摄高分辨率照片的最大次数，
  • $r$ 和 $c$：两个长度为 $n$ 的数组，描述网格中包含兴趣点的那些小方格的坐标。对于 $0 \le i \le n - 1$，第 $i$ 个兴趣点位于坐标为 $(r_i, c_i)$ 的小方格，
  • 这个函数应该返回被至少拍摄一次的小方格的总数的最小值（这些照片必须覆盖所有兴趣点）。

样例一

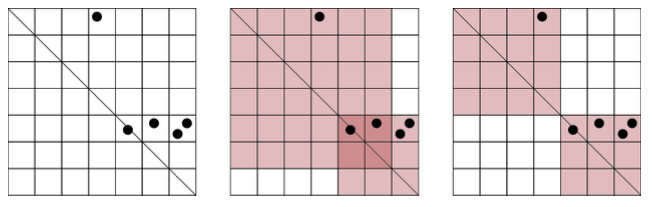
take_photos(5, 7, 2, [0, 4, 4, 4, 4], [3, 4, 6, 5, 6])

在这个样例中，我们有一个 $7 \times 7$ 的网格，其中含有 $5$ 个兴趣点。这些兴趣点位于 $4$ 个不同的小方格中：$(0, 3)$，$(4, 4)$，$(4, 5)$ 和 $(4, 6)$。你最多可以拍摄 $2$ 次高分辨率照片。

能够拍摄到所有 $5$ 个兴趣点的一种方法是拍这样两张照片：一张照片是选取大小为 $6 \times 6$ 的正方形并包含小方格 $(0, 0)$ 和 $(5, 5)$，另一张照片是选取大小为 $3 \times 3$ 的正方形并包含小方格 $(4, 4)$ 和 $(6, 6)$。如果我们拍摄这两张照片的话，卫星将传送 $41$ 个小方格的数据，这个不是最优解。

在最优解中，一张照片拍摄一个大小为 $4\times 4$ 的正方形并包含小方格 $(0, 0)$ 和 $(3, 3)$，另一张照片则拍摄一个大小为 $3 \times 3$ 的正方形并包含小方格 $(4, 4)$ 和 $(6, 6)$。这样被拍摄到的小方格只有 $25$ 个，它是最优的，因此 take_photos 应该返回 $25$。

注意：尽管小方格 $(4, 6)$ 上包含 $2$ 个兴趣点，但该小方格进需要被拍摄一次就足够。样例一的拍摄方法如下图所示。左边的图表示这个样例中对应的方格，中间的图表示一个次优解，它总共拍摄了 $41$ 个小方格。而右边的图则表示最优解。

样例二

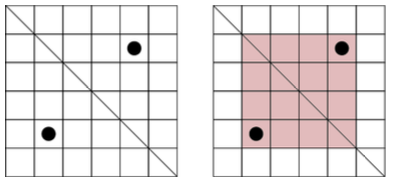
take_photos(2, 6, 2, [1, 4], [4, 1])

在这个样例中有 $2$ 个对称的兴趣点：分别位于小方格 $(1, 4)$ 和小方格 $(4, 1)$。任何一张包含其中一个兴趣点的正确照片也必然包含另一个兴趣点，因此，拍摄一张照片便已经足够。

下图表示了样例二和它的最优解，在这个解中卫星只拍摄了一张包含 $16$ 个小方格的照片。

子任务

在全部子任务中， $1 \le k \le n$。

评测方式

评测程序将会按照下列格式读取输入数据：

• 第 $1$ 行：整数 $n, m$ 和 $k$，
• 第 $2 + i~(0 \le i \le n - 1)$ 行：整数 $r_i$ 和 $c_i$。

交互式类型的题目怎么本地测试

时间限制：$2\texttt{s}$

空间限制：$2\texttt{GB}$

下载

样例及测评库下载