这天，跳蚤国王决定亲自下江南视察当地跳蚤的生活情况。

江南一共有 $n$ 座城市编号为$1$到 $n$，城市之间有一些道路相连。其道路结构可以抽象为一棵仙人掌。如果一个无向连通图的任意一条边最多属于一个简单环，我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。

现在跳蚤国王在$1$号城市准备出发。为了制定合理的下江南路线，跳蚤国王时不时问他的助手伏特：“从$1$号城市出发经过恰好 $l$ 条道路的简单路径有多少条？”。所谓简单路径即不经过重复的结点的路径。

这可难倒了伏特，请你对于 $l = 1, 2, \dots, (n-1)$ 求出相应的答案。只用输出答案对 $998244353$（$7 \times 17 \times 2^{23} + 1$，一个质数）取模后的值。

输入格式

第$1$行两个正整数$n, m$表示城市的个数和道路的条数。保证$n \geq 2$。

接下来$m$行每行两个正整数$v, u$（$1 \leq v, u \leq n$）表示一条连接城市$v$和$u$的道路。

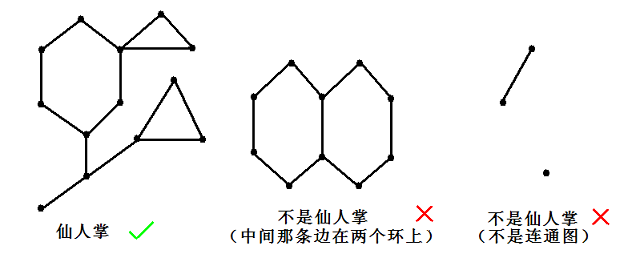
保证输入的图是一棵仙人掌，保证没有自环，但可能有重边。

输出格式

输出 $n - 1$ 行，第 $i$ 行包含一个整数表示 $l = i$ 时的答案（$1 \leq i \leq n - 1$）。

样例一

input

3 3
1 2
2 3
3 1

output

2
2

explanation

这是一个三元环，从 $1$ 号点出发走 $l$ 条边有顺时针走和逆时针走两种方式。

样例二

input

10 13
1 3
5 8
5 10
2 8
9 6
9 6
2 1
9 4
5 2
4 5
3 2
7 10
10 9

output

2
4
6
9
14
16
8
1
0

样例三

input

2 2
1 2
1 2

output

2

explanation

注意可能有重边。

样例四

输入输出数据见样例数据下载。另外，里面附有一张png图片作为该样例的解释。

限制与约定

虽然我没有给 $m$ 的范围，但是熟悉仙人掌的小朋友都知道对于仙人掌肯定满足 $n - 1 \leq m \leq 2n - 2$。

时间限制：$1\texttt{s}$

空间限制：$256\texttt{MB}$

下载

样例数据下载