【NOI2016】区间 - 题目 - Universal Online Judge

在数轴上有 $n$ 个闭区间 $[l_{1}, r_{1}], [l_{2}, r_{2}], . . ., [l_{n}, r_{n}]$ 。现在要从中选出 $m$ 个区间，使得这 $m$ 个区间共同包含至少一个位置。换句话说，就是使得存在一个 $x$ ，使得对于每一个被选中的区间 $[l_{i}, r_{i}]$ ，都有 $l_{i} \leq x \leq r_{i}$ 。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 $[l_{i}, r_{i}]$ 的长度定义为 $r_{i} - l_{i}$ ，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 $- 1$ 。

输入格式

第一行包含两个正整数 $n, m$ ，用空格隔开，意义如上文所述。保证 $1 \leq m \leq n$ 。

接下来 $n$ 行，每行表示一个区间，包含用空格隔开的两个整数 $l_{i}$ 和 $r_{i}$ 为该区间的左右端点。

输出格式

只有一行，包含一个正整数，即最小花费。

样例一

input

output

explanation

样例图

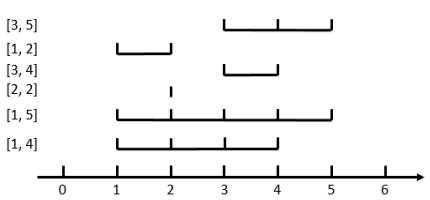
如图，当 $n = 6, m = 3$ 时，花费最小的方案是选取 $[3, 5]$ 、 $[3, 4]$ 、 $[1, 4]$ 这三个区间，他们共同包含了 $4$ 这个位置，所以是合法的。其中最长的区间是 $[1, 4]$ ，最短的区间是 $[3, 4]$ ，所以它的花费是 $(4 - 1) - (4 - 3) = 2$ 。

样例二

见样例数据下载。

样例三

见样例数据下载。

限制与约定

所有测试数据的范围和特点如下表所示：

测试点编号	$n$	$m$	$l_{i}, r_{i}$
1	$20$	$9$	$0 \leq l_{i} \leq r_{i} \leq 100$
2	$20$	$10$	$0 \leq l_{i} \leq r_{i} \leq 100$
3	$199$	$3$	$0 \leq l_{i} \leq r_{i} \leq 100000$
4	$200$	$3$
5	$1000$	$2$
6	$2000$	$2$
7	$199$	$60$	$0 \leq l_{i} \leq r_{i} \leq 5000$
8	$200$	$50$	$0 \leq l_{i} \leq r_{i} \leq 5000$
9	$200$	$50$	$0 \leq l_{i} \leq r_{i} \leq 10^{9}$
10	$1999$	$500$	$0 \leq l_{i} \leq r_{i} \leq 5000$
11	$2000$	$400$	$0 \leq l_{i} \leq r_{i} \leq 5000$
12	$2000$	$500$	$0 \leq l_{i} \leq r_{i} \leq 10^{9}$
13	$30000$	$2000$	$0 \leq l_{i} \leq r_{i} \leq 100000$
14	$40000$	$1000$
15	$50000$	$15000$
16	$100000$	$20000$
17	$200000$	$20000$	$0 \leq l_{i} \leq r_{i} \leq 10^{9}$
18	$300000$	$50000$
19	$400000$	$90000$
20	$500000$	$200000$

时间限制： $3 s$

空间限制： $256 MB$

下载

样例数据下载

Universal Online Judge

UOJ

#222. 【NOI2016】区间