sylvia 是一个热爱学习的女孩子，今天她想要学习线段树技巧。

但是因为 sylvia 是还是萌新，所以她一不小心将线段树写成了奇怪的形状：

在正常的线段树中，对于区间 $[l,r]$，我们会取 $m=\lfloor \frac{l+r}{2} \rfloor$，然后将这个区间分成 $[l,m]$ 和 $[m+1,r]$ 两个子区间。

但是，sylvia 的线段树却不是这样的，她用了一种不可描述的方式取了 $m$ 的值（当然 $m$ 还是满足 $l \leq m < r$ 的），以至于整棵树的形状非常奇怪。

奇怪归奇怪，这棵线段树仍然是可以进行线段树的操作的，就比如下面这棵在 $[1,6]$ 上建的奇怪的线段树，我们仍然可以用传统的线段树算法定位出一些区间（只不过不再满足 $\log$ 的复杂度了），以区间 $[2,4]$ 为例，那么定位的过程如蓝色箭头所示，经过的节点为蓝色节点。

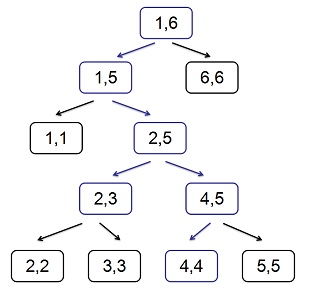
现在 sylvia 建出了一棵奇怪的线段树，最开始所有点都是白色的。接着 sylvia 对这棵线段树进行了若干次操作，每次操作都给出了一个区间 $[l,r]$ 并在线段树上定位出这个区间，在定位的同时，它把经过的节点都染黑了（本来就是黑的节点仍然保持黑色）。

例如对上面这棵线段树，第一次操作为 $[2,4]$，那么在操作后所有蓝色节点都被染黑了。

但是因为 sylvia 是一个健忘的女孩子，过了一段时间后，她已经忘了她到底进行了哪些操作，但是幸运的是最终的线段树还是被保留了下来。

现在 sylvia 想要知道她最少进行多少次操作，才能将本来全白的线段树变成现在这样。

输入格式

输入第一行一个正整数 $n$ 表示线段树的根节点为 $[1,n]$。

接下来 $2n-1$ 行按照线段树的先序遍历描述了每一个节点，如果这个节点是叶子节点，那么这一行只有一个整数 $t_i$，否则这一行有两个整数 $t_i$ 和 $m_i$。

其中 $t_i$ 如果是 $1$ 表示这个节点是黑色的，否则表示这个点是白色的。$m_i$ 表示建树时这个节点划分子区间的临界点，如果当前区间为 $[l_i,r_i]$，保证 $l_i\leq m_i< r_i$。

聪明的 sylvia 发现给出这些信息是可以唯一确定一棵奇怪的线段树的，所以她决定就以这种格式来告诉你这些信息。

输出格式

输出一行表示答案，因为 sylvia 是一个粗心的女孩子，所以可能存在无解的情况，这时只要输出 OwO 就好了。

样例一

input

2
1 1
1
1

output

2

explanation

最优解为对区间 $[1,1]$ 和 $[2,2]$ 进行操作。

样例二

input

2
0 1
1
1

output

OwO

样例三

input

9
1 5
1 3
1 2
1 1
0
1
1
1 4
0
0
1 7
1 6
1
0
1 8
1
0

output

2

explanation

最优解为对区间 $[2,8]$ 和 $[6,6]$ 进行操作。

样例四

见样例数据下载。

限制与约定

由于一些原因，本题使用捆绑测试。每个子任务有若干个测试点，分为 $5$ 个子任务，你只有通过一个子任务的所有测试点才能得到这个子任务的分数。

时间限制：$1\texttt{s}$

空间限制：$256\texttt{MB}$

下载

样例数据下载