烟花表演是最引人注目的节日活动之一。在表演中,所有的烟花必须同时爆炸。为了确保安全，烟花被安置在远离开关的位置上，通过一些导火索与开关相连。导火索的连接方式形成一棵树，烟花是树叶，如图所示。火花从开关出发，沿导火索移动。每当火花抵达一个分叉点时，它会扩散到与之相连的所有导火索，继续燃烧。导火索燃烧的速度是一个固定常数。图中展示了六枚烟花 $\{E_1,E_2,\dots ,E_6\}$ 的连线布局，以及每根导火索的长度。图中还标注了当在时刻 $0$ 从开关点燃火花时，每一发烟花的爆炸时间。

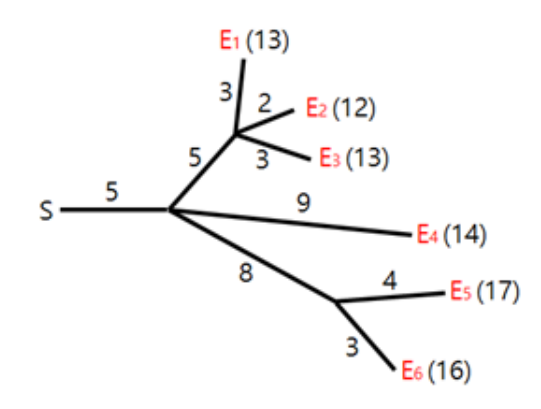
Hyunmin 为烟花表演设计了导火索的连线布局。不幸的是，在他设计的布局中，烟花不一定同时爆炸。我们希望修改一些导火索的长度，让所有烟花在同一时刻爆炸。例如，为了让图中的所有烟花在时刻 $13$ 爆炸，我们可以像下图中左边那样调整导火索长度。类似地，为了让图中的所有烟花在时刻 $14$ 爆炸，我们可以像下图中右边那样调整长度。

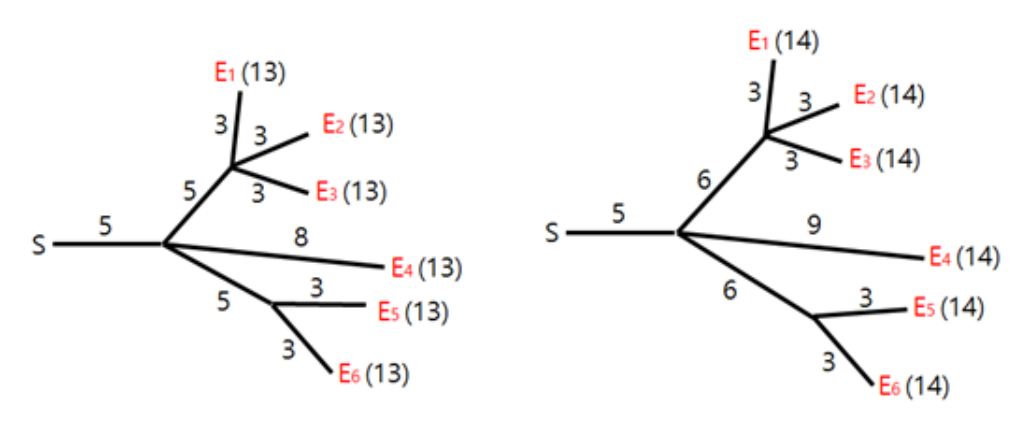
修改导火索长度的代价等于修改前后长度之差的绝对值。例如，将上面那副图中布局修改为下面那副图的左边布局的总代价为 $6$，而修改为右边布局的总代价为 $5$。

导火索的长度可以被减为 $0$，同时保持连通性不变。

给定一个导火索的连线布局，你需要编写一个程序，去调整导火索长度，让所有的烟花在同一时刻爆炸，并使得代价最小。

输入格式

所有的输入均为正整数。令 $N$ 代表分叉点的数量，$M$ 代表烟花的数量。分叉点从 $1$ 到 $N$ 编号，编号为 $1$ 的分叉点是开关。烟花从 $N+1$ 到 $N+M$ 编号。

输入第一行为 $N,M$。后面 $N+M-1$ 行，第 $i$ 行两个整数 $P_{i+1},C_{i+1}$。其中 $P_i$ 满足 $1\le P_i<i$，代表和分叉点或烟花 $i$ 相连的分叉点。$C_i$ 代表连接它们的导火索长度（$1\le C_i\le {10}^9$）除开关外，每个分叉点和多于 $1$ 条导火索相连，而每发烟花恰好与 $1$ 条导火索相连。

输出格式

输出调整导火索长度，让所有烟花同时爆炸，所需要的最小代价。

样例一

input

4 6
1 5
2 5
2 8
3 3
3 2
3 3
2 9
4 4
4 3

output

5

限制与约定

子任务 1（7 分）：$N=1$，$1\le M\le 100$。

子任务 2（19 分）：$1\le N+M\le 300$，且开关到任一烟花的距离不超过 $300$。

子任务 3（29 分）：$1\le N+M\le 5000$。

子任务 4（45 分）：$1\le N+M\le 300000$。

时间限制：$1\mathtt{\text{s}}$

空间限制：$256\mathtt{\text{MB}}$

下载

样例数据下载